北师大版八年级数学上册第四章 一次函数4 .4一次函数的应用(3)教学设计
文档属性
| 名称 | 北师大版八年级数学上册第四章 一次函数4 .4一次函数的应用(3)教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 553.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览

文档简介
一次函数的应用(3)教学设计
(选自八年级上册第四章《一次函数》第四节)
1、 教材分析
本节课是北师大版八年级上册第四章《一次函数》第四节《一次函数的应用》的第三课时,主要是利用两个一次函数的图象解决一些生活中的实际问题,和前一课时一样,教科书注重从函数图象中获取信息从而解决具体问题,关注数形结合思想的揭示,关注形象思维能力的发展。
本节内容是继七年级上册《整式及其加减》“数值转换机”——第一次渗透函数思想,七年级下册《变量之间的关系》——第一次集中讨论变量之间的关系后,对教材对函数教学的进一步深化,也是二元一次方程组、反比例函数、二次函数等内容的学习基础,甚至是高中、大学学段中函数概念的提前渗透。所以,函数的学习是循序渐进、螺旋上升的,贯穿初中数学学习的始终。
2、 学情分析
作为本章最后一节课,学生已经学习了一次函数的概念、一次函数的图象、一次函数的图像特征,并且了解到一次函数的应用十分广泛。在此基础上,通过生活中熟悉的实际问题,进一步探讨一次函数的应用,对整章内容的总体复习。
3、 教学目标
1、 进一步训练学生的识图能力,能通过函数图象获取信息,解决简单的实际问题;
2、 在函数图象信息获取过程中,进一步培养学生的数形结合意识,发展形象思维;
3、 在解决实际问题过程中,进一步发展学生分析问题、解决问题的能力和数学应用意识;
4、 在实际问题的解决过程中,使学生初步认识数学与生活的密切联系,从而培养学生学习数学的兴趣。
4、 教学重难点
重点:利用一次函数分析、解决简单实际问题,发展数形结合的思想。
难点:从一次函数图象中正确读取信息。
5、 教法学法
教学方法:“熟悉的问题情境——建立数学函数模型——应用与拓展”,结合问题情境,利用有层次的问题串引导学生进行探究和思考,坚持坚持以学生为主体,以教师为主导。
教具:教材、讲学稿
学具:教材、讲学稿、铅笔、直尺
6、 教学过程
本课教学设计共5个环节:前情回顾、探究导入、合作探究、课堂小结、巩固练习。
1. 前情回顾
在手机“待机”情况下,手机电池剩余电量百分比y是使用
时间x(小时)的一次函数关系,如右图:
(1)手机开机时电池电量百分比为
(2)预测在“待机”情况下手机最多能维持多长时间?
(设计意图:通过学生熟悉的手机电量问题,引导学生感知实际问题中蕴藏的一次函数知识,通过复习旧知,唤醒活动探究、数形结合的经验,为后续教学做铺垫。)
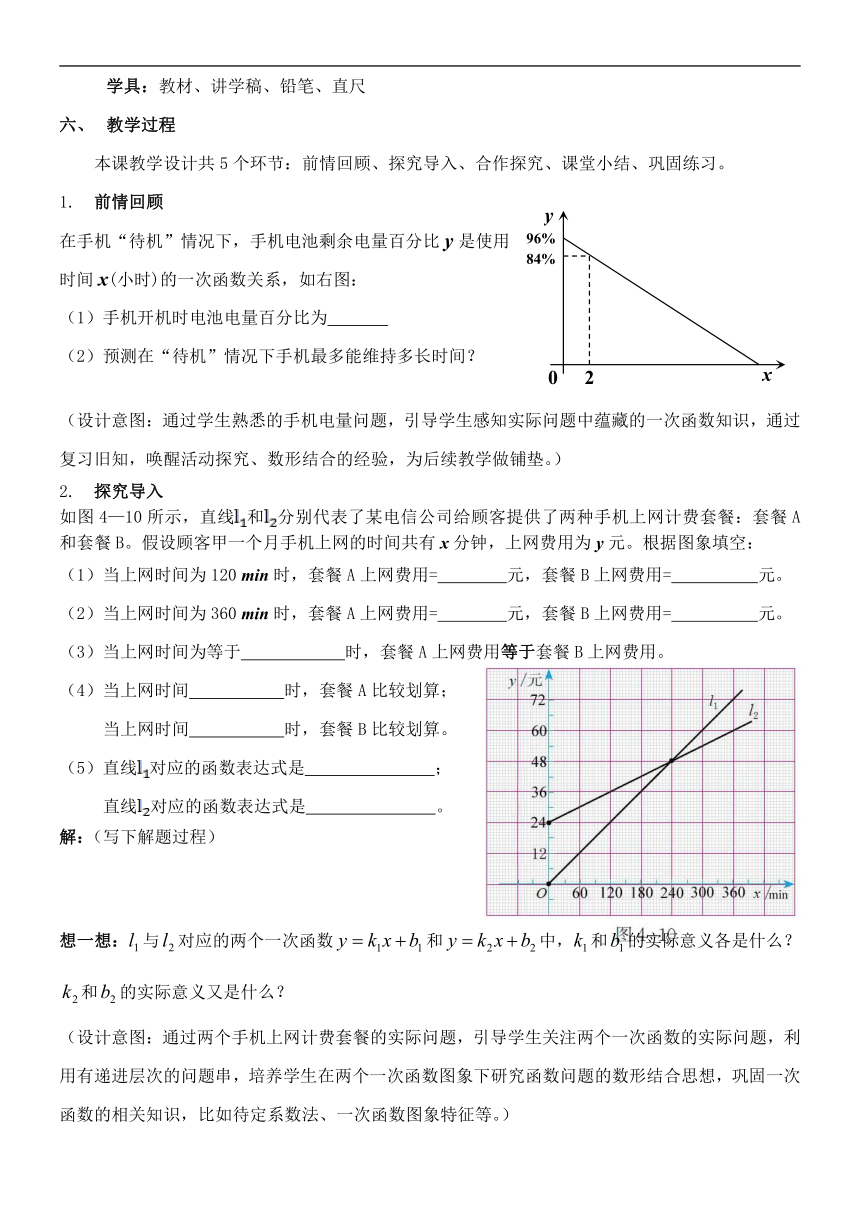
2. 探究导入
如图4—10所示,直线和分别代表了某电信公司给顾客提供了两种手机上网计费套餐:套餐A和套餐B。假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元。根据图象填空:
(1)当上网时间为120 min时,套餐A上网费用= 元,套餐B上网费用= 元。
(2)当上网时间为360 min时,套餐A上网费用= 元,套餐B上网费用= 元。
(3)当上网时间为等于 时,套餐A上网费用等于套餐B上网费用。
(4)当上网时间 时,套餐A比较划算;
当上网时间 时,套餐B比较划算。
(5)直线对应的函数表达式是 ;
直线对应的函数表达式是 。
解:(写下解题过程)
想一想:与对应的两个一次函数和中,和的实际意义各是什么?和的实际意义又是什么?
(设计意图:通过两个手机上网计费套餐的实际问题,引导学生关注两个一次函数的实际问题,利用有递进层次的问题串,培养学生在两个一次函数图象下研究函数问题的数形结合思想,巩固一次函数的相关知识,比如待定系数法、一次函数图象特征等。)
3. 合作探究
例3 在某一集《跑男》中,铁瓷组合(李晨、鹿晗)按照任务追击王祖蓝一人。铁瓷组合到达任务地点后迅速对王祖蓝进行追赶(如图4-12),图中,分别表示铁瓷组合、王祖蓝相对于铁瓷组合出发地点的距离(米)与追赶时间(分)之间的关系。
根据图象回答下列问题:
(1)哪条线表示铁瓷组合距出发地点的距离与时间之间的关系?
(2)铁瓷组合和王祖蓝哪个队伍的速度快?
(3)照此速度,如果一直追下去,那么铁瓷组合能否追上王祖蓝?能在150秒内追上王祖蓝?
(4)按照游戏规定,当王祖蓝逃到离出发地点500米的安全屋时,任何跑男成员都无法撕他名牌.照此速度,铁瓷组合能否在王祖蓝逃到安全屋前将其拦截?
(5)试求出与对应的两个一次函数和
想一想:
(1)与对应的两个一次函数和中,的实际意义各是什么?铁瓷组合和王祖蓝的行进速度各是多少?
(2)能用其他方法求出,的交点P吗?
(设计意图:利用学生熟悉的综艺节目问题,引导学生发现其中的数学问题,利用不完整的函数图象,进一步培养学生在两个一次函数图象下研究函数问题的数形结合思想。)
4. 课堂小结
本节课学习一次函数应用,在运用一次函数解决实际问题时,可从函数图象上获取信息解决问题,也可设法求出各自对应的函数关系式,然后借助关系式通过计算解决问题。
借助关系式解决问题时,首先判断关系式特征(是否一次函数).当确定是一次函数,可求出函数表达式,然后运用一次函数图象和性质,进一步探讨所需要的结果。
5. 巩固练习
【童话故事】
“龟兔赛跑”:兔子和乌龟同时从起点出发,比赛跑步,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边的小树下睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟已先到达终点.
【数学探究】
假设乌龟、兔子的速度及赛场均保持不变,图1刻画了“龟兔赛跑”的故事,其中(分)表示乌龟从起点出发所行的时间,(米)表示兔子所行的路程,(米)表示乌龟所行的路程.
(1)分别求线段、所表示的、与之间的函数关系式;
(2)试解释图中线段的实际意义;
(3)兔子输了比赛,心里很不甘心,它们约定再次赛跑,
①如果兔子让乌龟先跑30分钟,它才开始追赶,请在图2中画出兔子所行的路程与之间的函数关系的图象,并直接判断谁先到达终点;
②如果兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,它们同时出发,这一次谁先到达终点呢?为什么?
7、 课后反思
本节课是学生已经掌握了一次函数图象和有关性质的基础上,对有关知识进行应用和拓展,在教学过程中,教师应通过学生熟悉的问题情境的创设,激发学生的学习兴趣,感受一次函数等数学知识在生活中的应用,注重通过有层次的问题串设计,引导学生一步步发现图像中的信息,让学生从实际问题中逐步抽象出函数及一次函数的概念、图象特征、性质,进而在师生互动、生生交流的探究活动中,提高学生解决问题的能力。
y
x
96%
84%
2
0
(选自八年级上册第四章《一次函数》第四节)
1、 教材分析
本节课是北师大版八年级上册第四章《一次函数》第四节《一次函数的应用》的第三课时,主要是利用两个一次函数的图象解决一些生活中的实际问题,和前一课时一样,教科书注重从函数图象中获取信息从而解决具体问题,关注数形结合思想的揭示,关注形象思维能力的发展。
本节内容是继七年级上册《整式及其加减》“数值转换机”——第一次渗透函数思想,七年级下册《变量之间的关系》——第一次集中讨论变量之间的关系后,对教材对函数教学的进一步深化,也是二元一次方程组、反比例函数、二次函数等内容的学习基础,甚至是高中、大学学段中函数概念的提前渗透。所以,函数的学习是循序渐进、螺旋上升的,贯穿初中数学学习的始终。
2、 学情分析
作为本章最后一节课,学生已经学习了一次函数的概念、一次函数的图象、一次函数的图像特征,并且了解到一次函数的应用十分广泛。在此基础上,通过生活中熟悉的实际问题,进一步探讨一次函数的应用,对整章内容的总体复习。
3、 教学目标
1、 进一步训练学生的识图能力,能通过函数图象获取信息,解决简单的实际问题;
2、 在函数图象信息获取过程中,进一步培养学生的数形结合意识,发展形象思维;
3、 在解决实际问题过程中,进一步发展学生分析问题、解决问题的能力和数学应用意识;
4、 在实际问题的解决过程中,使学生初步认识数学与生活的密切联系,从而培养学生学习数学的兴趣。
4、 教学重难点
重点:利用一次函数分析、解决简单实际问题,发展数形结合的思想。
难点:从一次函数图象中正确读取信息。
5、 教法学法
教学方法:“熟悉的问题情境——建立数学函数模型——应用与拓展”,结合问题情境,利用有层次的问题串引导学生进行探究和思考,坚持坚持以学生为主体,以教师为主导。
教具:教材、讲学稿
学具:教材、讲学稿、铅笔、直尺
6、 教学过程
本课教学设计共5个环节:前情回顾、探究导入、合作探究、课堂小结、巩固练习。
1. 前情回顾
在手机“待机”情况下,手机电池剩余电量百分比y是使用
时间x(小时)的一次函数关系,如右图:
(1)手机开机时电池电量百分比为
(2)预测在“待机”情况下手机最多能维持多长时间?
(设计意图:通过学生熟悉的手机电量问题,引导学生感知实际问题中蕴藏的一次函数知识,通过复习旧知,唤醒活动探究、数形结合的经验,为后续教学做铺垫。)
2. 探究导入
如图4—10所示,直线和分别代表了某电信公司给顾客提供了两种手机上网计费套餐:套餐A和套餐B。假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元。根据图象填空:
(1)当上网时间为120 min时,套餐A上网费用= 元,套餐B上网费用= 元。
(2)当上网时间为360 min时,套餐A上网费用= 元,套餐B上网费用= 元。
(3)当上网时间为等于 时,套餐A上网费用等于套餐B上网费用。
(4)当上网时间 时,套餐A比较划算;
当上网时间 时,套餐B比较划算。
(5)直线对应的函数表达式是 ;
直线对应的函数表达式是 。
解:(写下解题过程)
想一想:与对应的两个一次函数和中,和的实际意义各是什么?和的实际意义又是什么?
(设计意图:通过两个手机上网计费套餐的实际问题,引导学生关注两个一次函数的实际问题,利用有递进层次的问题串,培养学生在两个一次函数图象下研究函数问题的数形结合思想,巩固一次函数的相关知识,比如待定系数法、一次函数图象特征等。)
3. 合作探究
例3 在某一集《跑男》中,铁瓷组合(李晨、鹿晗)按照任务追击王祖蓝一人。铁瓷组合到达任务地点后迅速对王祖蓝进行追赶(如图4-12),图中,分别表示铁瓷组合、王祖蓝相对于铁瓷组合出发地点的距离(米)与追赶时间(分)之间的关系。
根据图象回答下列问题:
(1)哪条线表示铁瓷组合距出发地点的距离与时间之间的关系?
(2)铁瓷组合和王祖蓝哪个队伍的速度快?
(3)照此速度,如果一直追下去,那么铁瓷组合能否追上王祖蓝?能在150秒内追上王祖蓝?
(4)按照游戏规定,当王祖蓝逃到离出发地点500米的安全屋时,任何跑男成员都无法撕他名牌.照此速度,铁瓷组合能否在王祖蓝逃到安全屋前将其拦截?
(5)试求出与对应的两个一次函数和
想一想:
(1)与对应的两个一次函数和中,的实际意义各是什么?铁瓷组合和王祖蓝的行进速度各是多少?
(2)能用其他方法求出,的交点P吗?
(设计意图:利用学生熟悉的综艺节目问题,引导学生发现其中的数学问题,利用不完整的函数图象,进一步培养学生在两个一次函数图象下研究函数问题的数形结合思想。)
4. 课堂小结
本节课学习一次函数应用,在运用一次函数解决实际问题时,可从函数图象上获取信息解决问题,也可设法求出各自对应的函数关系式,然后借助关系式通过计算解决问题。
借助关系式解决问题时,首先判断关系式特征(是否一次函数).当确定是一次函数,可求出函数表达式,然后运用一次函数图象和性质,进一步探讨所需要的结果。
5. 巩固练习
【童话故事】
“龟兔赛跑”:兔子和乌龟同时从起点出发,比赛跑步,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边的小树下睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟已先到达终点.
【数学探究】
假设乌龟、兔子的速度及赛场均保持不变,图1刻画了“龟兔赛跑”的故事,其中(分)表示乌龟从起点出发所行的时间,(米)表示兔子所行的路程,(米)表示乌龟所行的路程.
(1)分别求线段、所表示的、与之间的函数关系式;
(2)试解释图中线段的实际意义;
(3)兔子输了比赛,心里很不甘心,它们约定再次赛跑,
①如果兔子让乌龟先跑30分钟,它才开始追赶,请在图2中画出兔子所行的路程与之间的函数关系的图象,并直接判断谁先到达终点;
②如果兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,它们同时出发,这一次谁先到达终点呢?为什么?
7、 课后反思
本节课是学生已经掌握了一次函数图象和有关性质的基础上,对有关知识进行应用和拓展,在教学过程中,教师应通过学生熟悉的问题情境的创设,激发学生的学习兴趣,感受一次函数等数学知识在生活中的应用,注重通过有层次的问题串设计,引导学生一步步发现图像中的信息,让学生从实际问题中逐步抽象出函数及一次函数的概念、图象特征、性质,进而在师生互动、生生交流的探究活动中,提高学生解决问题的能力。
y
x
96%
84%
2
0
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
