人教版八年级上册11.1.1 三角形的边课件(共31张PPT)
文档属性
| 名称 | 人教版八年级上册11.1.1 三角形的边课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 22:26:53 | ||
图片预览









文档简介
(共31张PPT)
第11章 三角形
11.1.1 三角形的边
八年级数学上册·人教版
01
生活中的三角形
02
三角形的定义
03
三角形中的边
生活中的三角形
1
生活中的三角形
1
从古埃及的金字塔,到现代的隐形飞机,从生活中的自行车,到跨海大桥,我们都看到了什么形象?还能举出一些例子吗?
生活中的三角形
1
生活中常见的图案,它们都含有共同的图形——三角形
三角形的定义
2
三角形的定义
2
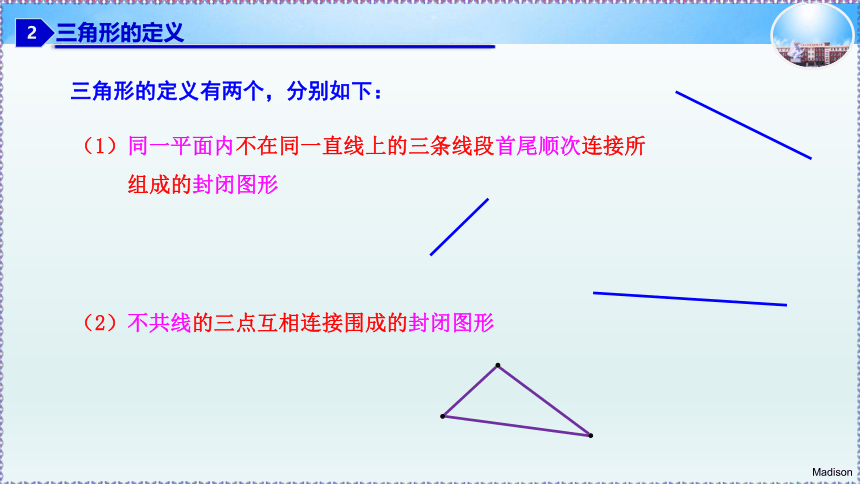
三角形的定义有两个,分别如下:
(1)同一平面内不在同一直线上的三条线段首尾顺次连接所
组成的封闭图形
(2)不共线的三点互相连接围成的封闭图形
三角形的定义
2
【答】当然不可以(定义难道是闹着玩的吗,可以随便改?)
原因如下:
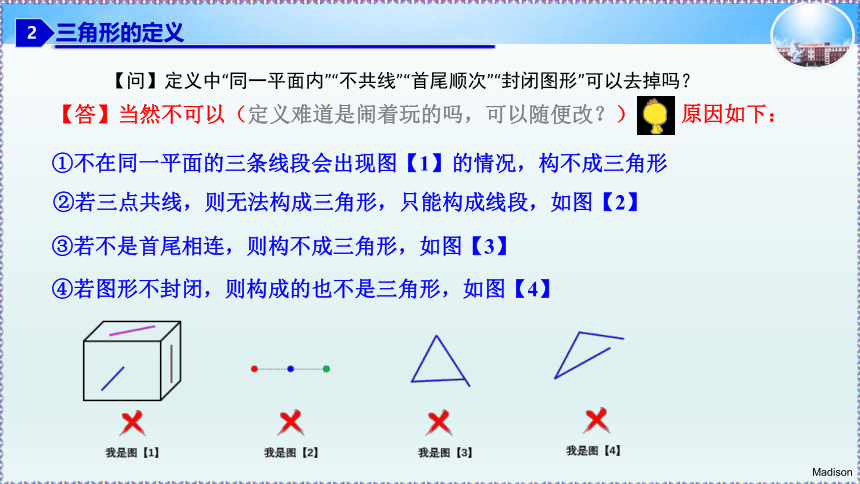
①不在同一平面的三条线段会出现图【1】的情况,构不成三角形
②若三点共线,则无法构成三角形,只能构成线段,如图【2】
③若不是首尾相连,则构不成三角形,如图【3】
④若图形不封闭,则构成的也不是三角形,如图【4】
三角形的定义
2
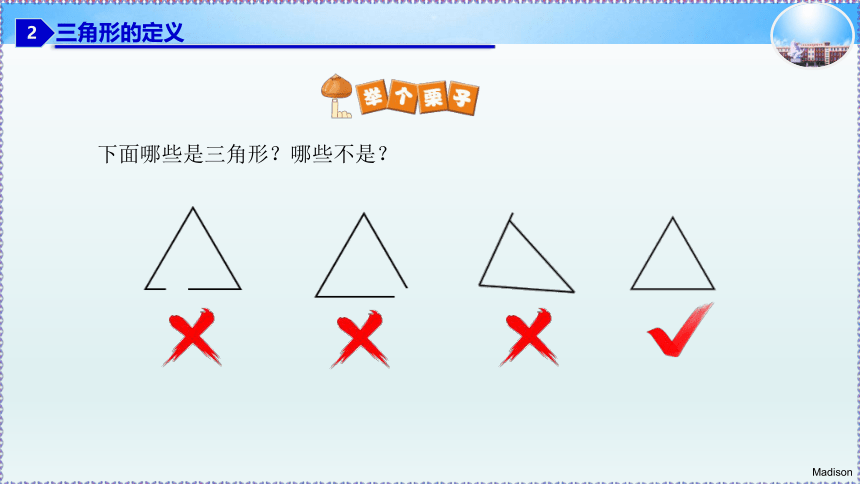
下面哪些是三角形?哪些不是?
三角形的有关概念
3
三角形的边
3
★组成三角形的线段叫做三角形的边,三角形有( )条边,分别是
★相邻两边组成的角叫做三角形的内角,三角形有( )个角,分别是
★相邻两边的公共端点叫做三角形的顶点,三角形有( )个顶点,分别是
顶点是A,B,C的三角形,记作: ABC
或表示为:△BCA或△CAB
三角形的分类
4
三角形的分类
4
我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.你能按照边的关系对三角形进行分类吗?
三边都不相等的三角形
三角形
等腰三角形
等边三角形
底边和腰不相等的等腰三角形
三角形的分类
4
腰
底
底角
顶角
按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
三角形的表示方法
4
三角形用顶点来命名,如图:
三角形三边关系
5
如图,任意画一个△ABC,一只小虫从点B 出发,沿三角形的边爬到点C,它有几条路线可以选择?各条线路的长一样吗?你能运用所学知识解释你的发现吗?由此你能推出三条边之间有怎样的关系?
B
C
A
AB + AC >BC, ①
AC + BC >AB, ②
AB + BC >AC. ③
即三角形两边的和大于第三边.
三角形的三边关系
5
三角形两边的差小于第三边.
由不等式②③移项可得 BC >AB -AC,
BC >AC -AB.由此你能得出什么结论?
B
C
A
三角形的三边关系
5
三角形的三边关系
5
★三角形的任意两边之和大于第三边(较短的两边之和大于最长边)
★三角形的任意两边之差小于第三边(最长边减去任意一个较短边的差大
于第三边)
★已知三角形的两边a,b(a≥b),第三边c的范围是_______________
三角形的三边关系
5
判断下列每组线段能否组成三角形(能的在括号中打“√”,不能的打“×”)
(1)a=5,b=4,c=3; ( )
(2)a=7,b=2,c=4; ( )
(3)a=6,b=6,c=12; ( )
(4)a=6,b=5,c=5。 ( )
√
×
×
√
图中有几个三角形?用符号表示出这些三角形.
题型①
——三角形的表示
图中的三角形有
ΔABC,ΔADC,ΔABE
ΔDBC,ΔDBF,
ΔEBC , ΔECF,
ΔFBC 一共8个三角形
现有两根长度分别是40和50的木棒,若要钉成一个三角形框架(不计接头处的损失),则在下列四根木棒中应该选取( )
A.长度为10的木棒 B.长度为40的木棒
C.长度为90的木棒 D.长度为100的木棒
题型②
——三角形三边长的关系
因为三角形两边之和大于第三边,则第三根木棒的长度应该是在50-40到50+40之间,即第三边L的范围是10<L<90,所以只有B选项正确.
【1】 下列各组长度的线段中,能组成三角形的是( )
A. 3cm,12cm,8cm B. 6cm,8cm,15cm
C. 2.5cm,3cm,5cm D. 6.3cm,6.3cm,12.6cm
根据三角形两边之和大于第三边,A,B,D均不满足,只有C选项满足较短两边之和大于最长边,故选C
【2】用一条长为18 cm 的细绳围成一个等腰三角形.
(1)如果腰长是底边的 2 倍,那么各边的长是多少?
解:设底边长为 x cm,则腰长为 2x cm.
x + 2x + 2x =18.
解得 x = 3.6.
所以,三边长分别为 3.6 cm,7.2 cm,7.2 cm.
因为4 + 4<10,不符合三角形两边的和大于第三边,所以不能围成腰长为 4 的等腰三角形.
由以上讨论可知,第①种情况可以围成底边长为4 cm的等腰三角形.
(2)能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
解:①如果 4 cm 长的边为底边,设腰长为 x cm,则
4 + 2x = 18. 解得 x = 7.
②如果 4 cm 长的边为腰,设底边长为x cm,则
4×2 + x = 18. 解得 x = 10.
【3】如图,在ΔABC中,AB=AC,D为AC上一点,
试说明2AC>(BD+CD)
因为AC=AD+CD,AB=AC
所以2AC=AB+AD+CD>BD+CD
在ΔABD中有AB+AD>BD
题型③
——求第三边的长度
已知三角形的一边长为 5 cm,另一边长为 3 cm .则第三边的长 x 的取值范围是________________.
2cm < x < 8cm
已知一个三角形的两边长分别为3cm和4cm,第三边的长度为s,如果s是奇数,那么s的值是________;这样的三角形有_____个;如果s是偶数,则s的值是________;这样的三角形又有_____个.
题型③
——求第三边的长度
因为三角形两边之和大于第三边,则第三边s的范围是
1<s<7,若s是奇数,那么s是3或者5,这样的三角形一共有2个;如果s是偶数,那么s是2,4或6,这样的三角形一共有3个
THANKS
“
”
第11章 三角形
11.1.1 三角形的边
八年级数学上册·人教版
01
生活中的三角形
02
三角形的定义
03
三角形中的边
生活中的三角形
1
生活中的三角形
1
从古埃及的金字塔,到现代的隐形飞机,从生活中的自行车,到跨海大桥,我们都看到了什么形象?还能举出一些例子吗?
生活中的三角形
1
生活中常见的图案,它们都含有共同的图形——三角形
三角形的定义
2
三角形的定义
2
三角形的定义有两个,分别如下:
(1)同一平面内不在同一直线上的三条线段首尾顺次连接所
组成的封闭图形
(2)不共线的三点互相连接围成的封闭图形
三角形的定义
2
【答】当然不可以(定义难道是闹着玩的吗,可以随便改?)
原因如下:
①不在同一平面的三条线段会出现图【1】的情况,构不成三角形
②若三点共线,则无法构成三角形,只能构成线段,如图【2】
③若不是首尾相连,则构不成三角形,如图【3】
④若图形不封闭,则构成的也不是三角形,如图【4】
三角形的定义
2
下面哪些是三角形?哪些不是?
三角形的有关概念
3
三角形的边
3
★组成三角形的线段叫做三角形的边,三角形有( )条边,分别是
★相邻两边组成的角叫做三角形的内角,三角形有( )个角,分别是
★相邻两边的公共端点叫做三角形的顶点,三角形有( )个顶点,分别是
顶点是A,B,C的三角形,记作: ABC
或表示为:△BCA或△CAB
三角形的分类
4
三角形的分类
4
我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.你能按照边的关系对三角形进行分类吗?
三边都不相等的三角形
三角形
等腰三角形
等边三角形
底边和腰不相等的等腰三角形
三角形的分类
4
腰
底
底角
顶角
按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
三角形的表示方法
4
三角形用顶点来命名,如图:
三角形三边关系
5
如图,任意画一个△ABC,一只小虫从点B 出发,沿三角形的边爬到点C,它有几条路线可以选择?各条线路的长一样吗?你能运用所学知识解释你的发现吗?由此你能推出三条边之间有怎样的关系?
B
C
A
AB + AC >BC, ①
AC + BC >AB, ②
AB + BC >AC. ③
即三角形两边的和大于第三边.
三角形的三边关系
5
三角形两边的差小于第三边.
由不等式②③移项可得 BC >AB -AC,
BC >AC -AB.由此你能得出什么结论?
B
C
A
三角形的三边关系
5
三角形的三边关系
5
★三角形的任意两边之和大于第三边(较短的两边之和大于最长边)
★三角形的任意两边之差小于第三边(最长边减去任意一个较短边的差大
于第三边)
★已知三角形的两边a,b(a≥b),第三边c的范围是_______________
三角形的三边关系
5
判断下列每组线段能否组成三角形(能的在括号中打“√”,不能的打“×”)
(1)a=5,b=4,c=3; ( )
(2)a=7,b=2,c=4; ( )
(3)a=6,b=6,c=12; ( )
(4)a=6,b=5,c=5。 ( )
√
×
×
√
图中有几个三角形?用符号表示出这些三角形.
题型①
——三角形的表示
图中的三角形有
ΔABC,ΔADC,ΔABE
ΔDBC,ΔDBF,
ΔEBC , ΔECF,
ΔFBC 一共8个三角形
现有两根长度分别是40和50的木棒,若要钉成一个三角形框架(不计接头处的损失),则在下列四根木棒中应该选取( )
A.长度为10的木棒 B.长度为40的木棒
C.长度为90的木棒 D.长度为100的木棒
题型②
——三角形三边长的关系
因为三角形两边之和大于第三边,则第三根木棒的长度应该是在50-40到50+40之间,即第三边L的范围是10<L<90,所以只有B选项正确.
【1】 下列各组长度的线段中,能组成三角形的是( )
A. 3cm,12cm,8cm B. 6cm,8cm,15cm
C. 2.5cm,3cm,5cm D. 6.3cm,6.3cm,12.6cm
根据三角形两边之和大于第三边,A,B,D均不满足,只有C选项满足较短两边之和大于最长边,故选C
【2】用一条长为18 cm 的细绳围成一个等腰三角形.
(1)如果腰长是底边的 2 倍,那么各边的长是多少?
解:设底边长为 x cm,则腰长为 2x cm.
x + 2x + 2x =18.
解得 x = 3.6.
所以,三边长分别为 3.6 cm,7.2 cm,7.2 cm.
因为4 + 4<10,不符合三角形两边的和大于第三边,所以不能围成腰长为 4 的等腰三角形.
由以上讨论可知,第①种情况可以围成底边长为4 cm的等腰三角形.
(2)能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
解:①如果 4 cm 长的边为底边,设腰长为 x cm,则
4 + 2x = 18. 解得 x = 7.
②如果 4 cm 长的边为腰,设底边长为x cm,则
4×2 + x = 18. 解得 x = 10.
【3】如图,在ΔABC中,AB=AC,D为AC上一点,
试说明2AC>(BD+CD)
因为AC=AD+CD,AB=AC
所以2AC=AB+AD+CD>BD+CD
在ΔABD中有AB+AD>BD
题型③
——求第三边的长度
已知三角形的一边长为 5 cm,另一边长为 3 cm .则第三边的长 x 的取值范围是________________.
2cm < x < 8cm
已知一个三角形的两边长分别为3cm和4cm,第三边的长度为s,如果s是奇数,那么s的值是________;这样的三角形有_____个;如果s是偶数,则s的值是________;这样的三角形又有_____个.
题型③
——求第三边的长度
因为三角形两边之和大于第三边,则第三边s的范围是
1<s<7,若s是奇数,那么s是3或者5,这样的三角形一共有2个;如果s是偶数,那么s是2,4或6,这样的三角形一共有3个
THANKS
“
”
