湘教版七年级下册 3.3 公式法(第1课时 )课件(共14张PPT)
文档属性
| 名称 | 湘教版七年级下册 3.3 公式法(第1课时 )课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
3.3 公式法
第1课时 用平方差公式因式分解
湘教版 七年级下册
1、什么叫把多项式分解因式
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
2、分解因式和整式乘法有何关系
多项式的分解因式与整式乘法互为逆运算.
3、已学过哪一种分解因式的方法
提公因式法
新课导入
1、能否用提公因式的方法把多项式x2-25,9x2-y2分解因式
提示:a2-b2=(a+b)(a-b)
9x2-y2
解:x2-25
= x2 - 52
=(x+5)(x-5)
=(3x)2-y2
=(3x+y)(3x-y)
利用平方差公式进行因式分解
推进新课
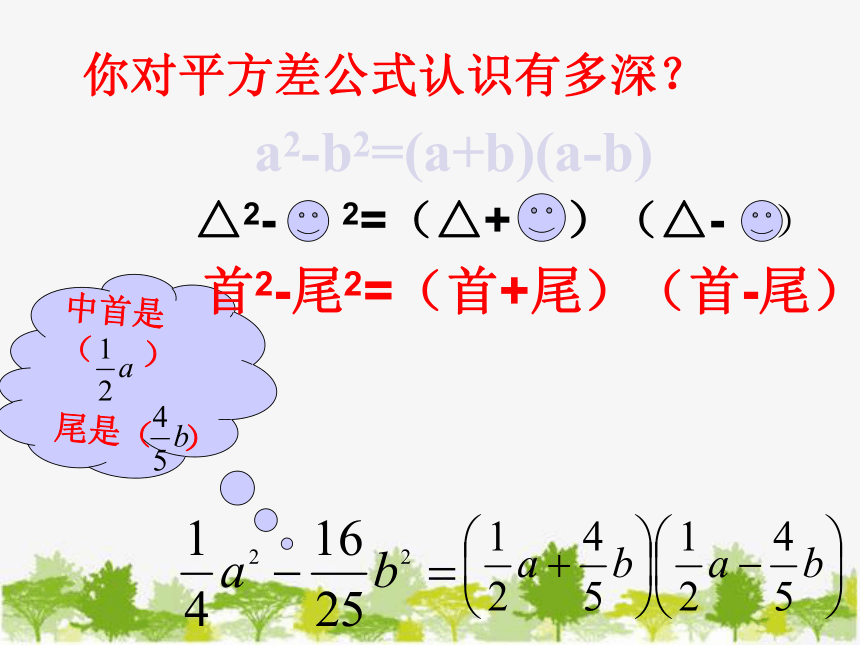
中首是( )
尾是( )
△2- 2=(△+ )(△- )
首2-尾2=(首+尾)(首-尾)
你对平方差公式认识有多深?
a2-b2=(a+b)(a-b)
(1) a2-1=( )2-( )2
(2) x4y2-4= ( )2-( )2
(3) 0.49x2-0.01y2=( )2-( )2
(4) 0.0001-121x2=( )2-( )2
2、口答下列各题:
3、能用平方差公式因式分解的多项式有何特征?
2
x2y
0.01
0.1y
11x
a
1
0.7x
①有且只有两个平方项;
②两个平方项异号;
1、下列哪些多项式可以用平方差公式分解因式?
(1) 4x2+y2; (2) 4x2-(-y)2;
(3) -4x2-y2; (4) -4x2+y2;
(5) a2-4; (6) a2+32.
随堂演练
2、把下列各式分解因式:
(1) 36-25x2
解:(1) 36-25x2
=62-(5x)2
=(6+5x)(6-5x)
(2) 16a2-9b2
(2) 16a2-9b2
=(4a)2-(3b)2
=(4a+3b)(4a-3b)
3、把多项式9(a+b)2-4(a-b)2分解因式.
解:9(a+b)2-4(a-b)2
=[3(a+b)]2-[2(a-b)]2
=[3(a+b)+2(a-b)]
[3(a+b)-2(a-b)]
=(3a+3b+2a-2b)
(3a+3b-2a+2b)
=(5a+b)(a+5b)
★平方差公式中字母a、b不仅可以表示数,而且也可以表示其它代数式.
4、把多项式x4-16分解因式.
解:x4-16
=(x2)2-42
=(x2+4)(x2-4)
★分解因式应分解到各因式都不能再分解为止.
=(x2+4)(x+2)(x-2)
★若多项式中有公因式,应先提取公因式,然后再进一步分解因式,直到不能分解为止.
解:2x3-8x
5、把多项式2x3-8x分解因式.
=2x (x2_22)
=2x (x+2)(x-2)
=2x (x2-4)
6、把下列各式分解因式:
(3) 9(m+n)2-(m-n)2
(1) a4–b4=
(2) (m2-3)2–1=
(a2)2-(b2)2=
(a2+b2)(a2-b2)
=(a2+b2)(a+b)(a-b)
(m2-3-1)(m2-3+1)
=(m2-4)(m2-2)
=(m+2)(m-2)(m2-2)
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
3.3 公式法
第1课时 用平方差公式因式分解
湘教版 七年级下册
1、什么叫把多项式分解因式
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
2、分解因式和整式乘法有何关系
多项式的分解因式与整式乘法互为逆运算.
3、已学过哪一种分解因式的方法
提公因式法
新课导入
1、能否用提公因式的方法把多项式x2-25,9x2-y2分解因式
提示:a2-b2=(a+b)(a-b)
9x2-y2
解:x2-25
= x2 - 52
=(x+5)(x-5)
=(3x)2-y2
=(3x+y)(3x-y)
利用平方差公式进行因式分解
推进新课
中首是( )
尾是( )
△2- 2=(△+ )(△- )
首2-尾2=(首+尾)(首-尾)
你对平方差公式认识有多深?
a2-b2=(a+b)(a-b)
(1) a2-1=( )2-( )2
(2) x4y2-4= ( )2-( )2
(3) 0.49x2-0.01y2=( )2-( )2
(4) 0.0001-121x2=( )2-( )2
2、口答下列各题:
3、能用平方差公式因式分解的多项式有何特征?
2
x2y
0.01
0.1y
11x
a
1
0.7x
①有且只有两个平方项;
②两个平方项异号;
1、下列哪些多项式可以用平方差公式分解因式?
(1) 4x2+y2; (2) 4x2-(-y)2;
(3) -4x2-y2; (4) -4x2+y2;
(5) a2-4; (6) a2+32.
随堂演练
2、把下列各式分解因式:
(1) 36-25x2
解:(1) 36-25x2
=62-(5x)2
=(6+5x)(6-5x)
(2) 16a2-9b2
(2) 16a2-9b2
=(4a)2-(3b)2
=(4a+3b)(4a-3b)
3、把多项式9(a+b)2-4(a-b)2分解因式.
解:9(a+b)2-4(a-b)2
=[3(a+b)]2-[2(a-b)]2
=[3(a+b)+2(a-b)]
[3(a+b)-2(a-b)]
=(3a+3b+2a-2b)
(3a+3b-2a+2b)
=(5a+b)(a+5b)
★平方差公式中字母a、b不仅可以表示数,而且也可以表示其它代数式.
4、把多项式x4-16分解因式.
解:x4-16
=(x2)2-42
=(x2+4)(x2-4)
★分解因式应分解到各因式都不能再分解为止.
=(x2+4)(x+2)(x-2)
★若多项式中有公因式,应先提取公因式,然后再进一步分解因式,直到不能分解为止.
解:2x3-8x
5、把多项式2x3-8x分解因式.
=2x (x2_22)
=2x (x+2)(x-2)
=2x (x2-4)
6、把下列各式分解因式:
(3) 9(m+n)2-(m-n)2
(1) a4–b4=
(2) (m2-3)2–1=
(a2)2-(b2)2=
(a2+b2)(a2-b2)
=(a2+b2)(a+b)(a-b)
(m2-3-1)(m2-3+1)
=(m2-4)(m2-2)
=(m+2)(m-2)(m2-2)
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
