2020-2021学年山东省烟台市开发区四年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2020-2021学年山东省烟台市开发区四年级(下)期末数学试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览




文档简介
2020-2021学年山东省烟台市开发区四年级(下)期末数学试卷
一、填空题。(共33分)
1.(4分)在1、2、6、9、19、21、23、42、99这些数中,奇数有 ,质数有 ,合数有 ,既是偶数又是合数的数有 。
2.(2分)把一根5米长的铁丝平均截成6段,每段占全长的 ,每段长 米。
3.(2分)同时是2和3的倍数的数,最小的两位数是 ,最大的两位数是 .
4.(2分)粮店里新进批面粉,第一天卖出这批面粉的,第二天卖出这批面粉的,第三天卖出这批面粉的。三天一共卖出这批面粉的 ,还剩 。
5.(1分)泰山比海平面高1545米,记作+1545米;吐鲁番盆地比海平面低154米,记作 米。
6.(3分)在横线上填上最简分数。
65cm2= dm2 800克= 千克 50分= 时
7.(2分)在横线上填上合适的数。
86000平方米= 公顷;2.05平方千米= 公顷。
8.(4分)在横线上填上“>”“<”或“=”。
0.625 2
9.(4分)=0.35= ÷120==63÷ 。
10.(2分)两个相邻奇数的和是12,它们的最大公因数是 ,最小公倍数是 。
11.(3分) 个是;里面有 个,有 个。
12.(2分)两个完全一样的梯形拼成了一个平行四边形,平行四边形的面积是7.8平方厘米,高是3厘米,则一个梯形的面积是 平方厘米,梯形的上、下两底的和是 厘米。
13.(2分)的分数单位是 ,再加上 个这样的分数单位就是最小的质数。
二、选择题。(在括号内将正确答案的序号涂黑)(共5分)
14.(1分)与方程0.5x=3的解相同的是( )
A.0.6x=3 B.5x+6=12 C.0.5x+5=8 D.2x﹣6=12
15.(1分)下列说法正确的是( )
A.等底等高的三角形面积一定相等
B.平行四边形的面积是三角形面积的2倍
C.直角三角形只有1条高
D.两个面积相等的三角形一定能拼成一个平行四边形
16.(1分)一个三角形和一个平行四边形面积相等,底也相等。已知平行四边形的高是18厘米,三角形的一条高是
( )
A.9厘米 B.36厘米 C.18厘米 D.6厘米
17.(1分)已知两个数的最大公因数是6,最小公倍数是90,若一个数是18,则另一个数是( )
A.90 B.15 C.18 D.30
18.(1分)要使是假分数,是真分数,x应是( )
A.1 B.15 C.16 D.无法确定
三、判断题。(正确的涂“√”,错误的涂“×”)(共5分)
19.(1分)长方形是轴对称图形,有四条对称轴.
20.(1分)一个合数至少有3个因数
21.(1分)当长方形和平行四边形的周长相等时,面积也相等. .
22.(1分)两个质数的乘积一定是合数. .
23.(1分)如果一个数是6的倍数,那么它一定是2和3的倍数.
四、计算。(共21分)
24.(5分)直接写得数。
+= ﹣= += ﹣=
+= ﹣= += ﹣=
﹣= +=
25.(10分)计算。
1﹣﹣ ﹣+
+﹣ ++
26.(6分)解方程。
3.8x+5.2x=52.2 8.5+1.6x=12.5 35.6﹣x=18.9
五、画一画。(4分)
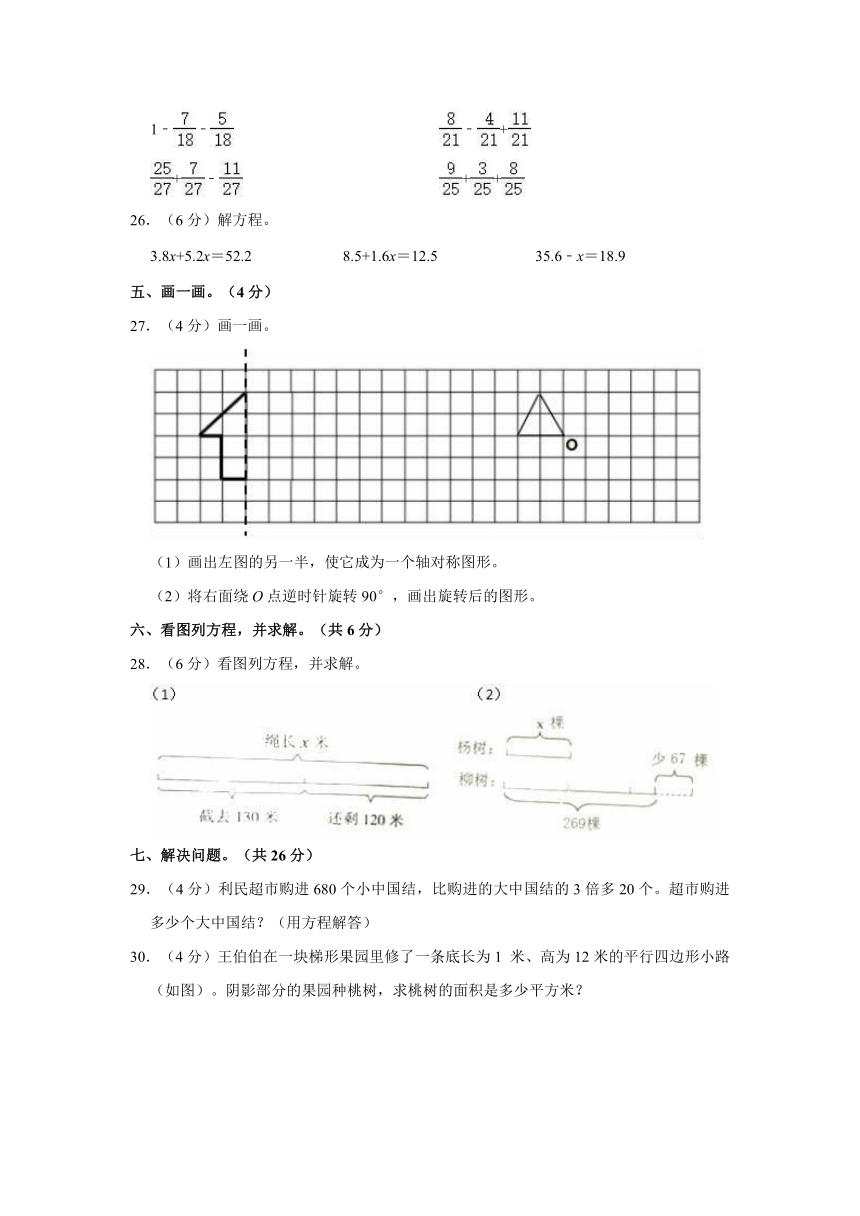
27.(4分)画一画。
(1)画出左图的另一半,使它成为一个轴对称图形。
(2)将右面绕O点逆时针旋转90°,画出旋转后的图形。
六、看图列方程,并求解。(共6分)
28.(6分)看图列方程,并求解。
七、解决问题。(共26分)
29.(4分)利民超市购进680个小中国结,比购进的大中国结的3倍多20个。超市购进多少个大中国结?(用方程解答)
30.(4分)王伯伯在一块梯形果园里修了一条底长为1 米、高为12米的平行四边形小路(如图)。阴影部分的果园种桃树,求桃树的面积是多少平方米?
31.(4分)王老师第一次到体育用品店买了26套运动服,第二次又买了同样的32套运动服,第二次比第一次多用了570元。每套运动服多少元?(用方程解答)
32.(4分)一件上衣和一条裤子的总价钱是325元,一件上衣的价钱是一条裤子的1.5倍。一件上衣和一条裤子分别是多少元?(用方程解答)
33.(4分)如图,菜园里有两块空地,计划种茄子和白菜。
(1)如果每棵茄子占地0.5平方米,这块茄子地可以种多少棵茄子?
(2)如果平均每平方米能收16千克白菜,这块白菜地能收多少千克白菜?
34.(6分)下面是某市2015~2019年参加义务植树活动人数统计表。
年份(年) 2015 2016 2017 2018 2019
人数(万人) 4 5 7 8 11
(1)根据上表中数据,完成下面折线统计图。
(2)根据折线统计图完成下面问题。
① 年参加义务植树的人数最多,有 万人,比最少的一年多 万人。
②平均每年参加义务植树的人数有 万人。
③通过统计图可以看出,参加义务植树的人数一直呈 趋势。
2020-2021学年山东省烟台市开发区四年级(下)期末数学试卷
参考答案与试题解析
一、填空题。(共33分)
1.【分析】偶数:是2的倍数的数叫作偶数;
奇数:不是2的倍数的数叫作奇数。
质数:一个数只有1和它本身两个因数,这个数叫作质数。
合数:指自然数中除了能被1和本身整除外,还能被其他的数整除的数。
“0”“1”既不是质数也不是合数。
【解答】解:在1、2、6、9、19、21、23、42、99这些数中,奇数有1、9、19、21、23、99,质数有2、18、23,合数有6、9、21、42、99,既是偶数又是合数的数有6、42。
故答案为:1、9、19、21、23、99;2、18、23;6、9、21、42、99;6、42。
【点评】此题主要考查了质数、合数、奇数、偶数的定义,要熟练掌握。
2.【分析】根据题意,把5米长的铁丝看作单位“1”,平均分成6段,每段就占6段的,求每段长多少米,利用全长除以段数即可。
【解答】解:1÷6=
5(米)
答:每段占全长的,每段长米。
故答案为:,。
【点评】此题重在区分分数在具体的题目中的区别:有些表示是某些量的几分之几,有些表示具体的数,做到正确区分,选择合适的解题方法。
3.【分析】同时是2和3的倍数的数一定是6的倍数,如6、12、18…,最小的两位数是12,因此得解;因为2和3最小公倍数是6,所以求既是3的倍数、又是2的倍数的最大两位数,即求100以内的6的最大倍数.
【解答】解:同时是2和3的倍数的数,最小的两位数是12,最大的两位数是96.
故答案为:12,96.
【点评】此题考查了找一个数的倍数的方法,明白同时是2和3的倍数,就是求6的倍数是解决此题的关键.
4.【分析】把这批面粉的总量看成单位“1”,第一天卖出这批面粉的,第二天卖出这批面粉的,第三天卖出这批面粉的,把这三个分率相加,即可求出一共卖出了这批面粉的几分之几;用单位“1”减去三天一共卖出这批面粉的分率,即可得剩下的。
【解答】解:
=
=
1﹣
答:三天一共卖出这批面粉的,还剩。
故答案为:,。
【点评】解决本题关键是理解把这批面粉的总量看成单位“1”,再根据分数加减法的意义求解。
5.【分析】用正负数表示意义相反的两种量:高于海平面记作正,则低于海平面就记作负。由此得解。
【解答】解:泰山比海平面高1545米,记作+1545米;吐鲁番盆地比海平面低154米,记作﹣154米。
故答案为:﹣154。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
6.【分析】低级单位平方厘米化高级单位平方分米除以进率100;
低级单位克化高级单位千克除以进率1000;
低级单位分化高级单位时除以进率60。
【解答】解:
65cm2=dm2 800克=千克 50分=时
故答案为:,,。
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。结果用分数表示时,通常化成最简分数。
7.【分析】根据1公顷=10000平方米,1平方千米=100公顷,解答此题即可。
【解答】解:86000平方米=8.6公顷;2.05平方千米=205公顷。
故答案为:8.6;205。
【点评】熟练掌握面积单位的换算,是解答此题的关键。
8.【分析】两个分数分别与1作差,差越小的原分数越大;先通分再比较大小;把分数化成小数,再比较大小;把带分数化成假分数,再根据同分母分数比较大小的方法进行比较。
【解答】解:因为1﹣=
1﹣=
因为
所以
因为=
所以<
因为=0.625
所以0.625=
因为2=<所以2<> <
0.625= 2<
故答案为:>,<,=,<。
【点评】熟练掌握用作差法比较分数大小的方法、异分母分数比较大小的方法、分数化成小数的方法以及带分数化成假分数的方法是解题的关键。
9.【分析】把0.35化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;都乘10就是;根据分数与除法的关系,=7÷20,再根据商不变的性质被除数、除数都乘6就是42÷120;都乘9就是63÷180。
【解答】解:=0.35=42÷120==63÷180。
故答案为:28,42,200,180。
【点评】此题主要是考查除法、小数、分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
10.【分析】先根据两个相邻奇数的和是12,求得这两个奇数为5和7,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积。
【解答】解:两个相邻奇数的和是12,则两个数为5和7
5和7的最大公因数是1,最小公倍数是5×7=35
故答案为:1,35。
【点评】考查了求几个数的最大公因数的方法与最小公倍数的方法:两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积。
11.【分析】已知一个数的几分之几是多少,求这个数用除法计算;再根据包含除法的意义,计算第二、第三小题。
【解答】解:
=
=6
=
=5
=
=10
答:6个是;里面有5个,有10个。
故答案为:6;5;10。
【点评】本题解题关键是根据分数除法的意义列出算式,再根据分数除法的计算法则,算出结果。
12.【分析】两个完全一样的梯形可以拼成一个平行四边形.这个平行四边形的面积是原来两个梯形面积的和,即为每个梯形面积的2倍,由“两个完全一样的梯形拼成的平行四边形面积是7.8平方厘米”可以求出一个梯形的面积,又因梯形的高已知,于是利用梯形的面积乘2,再除以梯形的高,即可求出上下底的和。
【解答】解:7.8÷2=3.9(平方厘米)
3.9×2÷3
=7.8÷3
=2.6(厘米)
答:一个梯形的面积是3.9平方厘米,梯形的上、下两底的和2.6厘米。
故答案为:3.9,2.6。
【点评】此题主要考查梯形的面积公式的推导过程,要注意两个完全一样的平面图形拼成一个图形,其面积就等于原图形的面积的2倍。
13.【分析】将单位“1”平均分成若干份,表示其中这样一份的数叫分数单位.由此可知,的分数单位是;最小的质数为2,2﹣=,里面有11个,所以再加上11个这样的分数单位就是最小的质数。
【解答】解:根据分数单位的意义可知,
的分数单位是;
2﹣=
所以再加上11个这样的分数单位就是最小的质数。
故答案为:,11。
【点评】一个分数的分母是几,其分数单位就是几分之一,分子是几,其就含有几个分数单位(带分数除外)。
二、选择题。(在括号内将正确答案的序号涂黑)(共5分)
14.【分析】先根据等式的基本性质,方程0.5x=3的两边同时除以0.5,求出x的值,再把x的值分别代入各选项中的方程,能使方程左边等于右边的就是与方程0.5x=3的解相同的方程。
【解答】解:0.5x=3
0.5x÷0.5=3÷0.5
x=6
A.把x=6代入方程0.6x=3,得:0.6×6=3.6≠方程右边,所以x=6不是该方程的解;
B.把x=6代入方程5x+6=12,得:5×6+6=36≠12,所以x=6不是该方程的解;
C.把x=6代入方程0.5x+5=8,得:0.5×6+5=8=方程右边,所以x=6是该方程的解;
D.把x=6代入方程2x﹣6=12,得:2×6﹣6=6≠12,所以x=6不是该方程的解。
故选:C。
【点评】熟练掌握方程的检验方法是解题的关键。
15.【分析】根据三角形的面积=底×高÷2可知:等底等高的三角形面积一定相等;等底等高的平行四边形的面积是三角形面积的2倍;任何三角形都有3条高;两个形状和大小都相同的三角形一定能拼成一个平行四边形,据此解答即可。
【解答】解:A.根据三角形的面积=底×高÷2可知:等底等高的三角形面积一定相等,题干说法正确;
B.等底等高的平行四边形的面积是三角形面积的2倍,题干说法是错误的;
C.任何三角形都有3条高,题干说法是错误的;
D.两个形状和大小都相同的三角形一定能拼成一个平行四边形,题干说法是错误的。
故选:A。
【点评】熟练掌握三角形和平行四边形的面积公式,三角形高的定义和画法,是解答此题的关键。
16.【分析】根据一个三角形和一个平行四边形面积相等,底也相等,那么三角形的高是平行四边形的高的2倍,据此解答即可。
【解答】解:18×2=36(厘米)
答:三角形的一条高是36厘米。
故选:B。
【点评】根据面积相等,底也相等的三角形和平行四边形底的倍数关系,解答此题即可。
17.【分析】用最小公倍数90除以已知数字18,得到所求数字的独有质因数的积,然后乘公有质因数的积(最大公约数6),即可得解.
【解答】解:90÷18=5
5×6=30
答:另一个数是30.
故选:D.
【点评】灵活应用“求最大公约数也就是这几个数的公有质因数的连乘积,最小公倍数是共有质因数与独有质因数的连乘积”的逆运算来求另一个数.
18.【分析】假分数是分子大于或等于1的分数,真分数小于1,分子比分母小,据此解答。
【解答】解:若是假分数,那么x可以等于分母15或大于15;
若是真分数,那么分子x必须小于分母16。
根据以上分析,x=15符合题意。
故选:B。
【点评】本题考查了真分数和假分数的定义。
三、判断题。(正确的涂“√”,错误的涂“×”)(共5分)
19.【分析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴,据此即可进行判断.
【解答】解:长方形是轴对称图形,有2条对称轴,故原题说法错误;
故答案为:×.
【点评】解答此题的主要依据是:轴对称图形的意义及特征.
20.【分析】自然数中,除了1和它本身外,还有别的因数的数为合数.由此可知,合数除了1和它本身外,至少还要有一个因数,即至少有3个因数,如9有1,9,3三个因数.
【解答】解:根据合数的意义可知,
合数除了1和它本身外,至少还要有一个因数,即至少有3个因数.
所以一个合数至少有3个因数说法正确.
故答案为:√.
【点评】根据合数的意义进行确定是完成本题的关键.
21.【分析】当长方形和平行四边形的周长相等时,则它们的边长可能相等,但高不一定相等,所以面积就不一定相等.
【解答】解:因为当长方形和平行四边形的周长相等时,
则它们的边长可能相等,但高不一定相等,所以面积也就不一定相等;
故答案为:×.
【点评】此题主要考查长方形和平行四边形的周长及面积计算公式.
22.【分析】根据质数与合数的定义即可做出判断.
【解答】解:质数只有两个约数,合数至少有三个约数,两个质数的乘积至少有四个约数,如2×3=6,6的约数有1、2、3、6;3×5=15,15的约数有1、3、5、15;2×5=10,10的约数有1、2、5、10.等等.
答:两个质数的乘积一定是合数.
故此题正确.
【点评】此题考查目的是对质数、合数定义的理解.
23.【分析】把6分解因数发现,2和3都是6的因数,所以一个数是6的倍数,那么它一定是2和3的倍数.
【解答】解:6=2×3,
6是2和3的倍数,所以一个数是6的倍数,那么它一定是2和3的倍数.
原题说法正确.
故答案为:√.
【点评】此题主要考查了因数和倍数的意义,注意知识的灵活运用.
四、计算。(共21分)
24.【分析】根据同分母分数相加(减),分子进行相加(减)得数作分子,分母不变,计算即可,注意结果化到最简。
【解答】解:
+= ﹣= += ﹣=
+=1 ﹣= += ﹣=
﹣= +=
【点评】考查了同分母分数的加法和减法运算,关键是熟练掌握计算法则正确进行计算。
25.【分析】根据同分母分数相加(减),分子进行相加(减)得数作分子,分母不变,计算即可,注意结果要化到最简。
【解答】解:1﹣﹣
=
=
﹣+
=
=
+﹣
=
=
++
=
=
【点评】考查了同分母分数的加法和减法运算,关键是熟练掌握计算法则正确进行计算。
26.【分析】(1)先把方程左边化简为9x,两边再同时除以9;
(2)方程两边同时减去8.5,两边再同时除以1.6;
(3)方程两边同时加上x,两边再同时减去18.9。
【解答】解:(1)3.8x+5.2x=52.2
9x=52.2
9x÷9=52.2÷9
x=5.8
(2)8.5+1.6x=12.5
8.5+1.6x﹣8.5=12.5﹣8.5
1.6x=4
1.6x÷1.6=4÷1.6
x=2.5
(3)35.6﹣x=18.9
35.6﹣x+x=18.9+x
18.9+x﹣18.9=35.6﹣18.9
x=16.7
【点评】熟练掌握等式的基本性质是解题的关键。
五、画一画。(4分)
27.【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出左半图的关键对称点,依次连接即可。
(2)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【解答】解:根据题意画图如下:
【点评】作旋转一定度数后的图形、作轴对称图形,对应点(对称点)位置的确定是关键。
六、看图列方程,并求解。(共6分)
28.【分析】(1)根据图意,题中的等量关系是:绳子的总长度﹣截去的米数=还剩下的米数,根据这个等量关系,列方程解答。
(2)从图上可得:柳树的棵数比杨树的3倍少67棵,所以它们之间的数量关系为:杨树棵数×3﹣67=柳树的棵树,根据这个等量关系,列方程解答即可。
【解答】解:(1)x﹣130=120
x﹣130+130=120+130
x=250
答:绳长250米。
(2)3x﹣67=269
3x﹣67+67=269+67
3x=336
3x÷3=336÷3
x=112
答:杨树有112棵。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系。
七、解决问题。(共26分)
29.【分析】根据“小中国结比购进的大中国结的3倍多20个”,可以提炼这道题的等量关系是:大中国结的个数×3+20个=小中国结的个数,根据这个等量关系列方程解答。
【解答】解:设超市购进x个大中国结。
3x+20=680
3x+20﹣20=680﹣20
3x=660
3x÷3=660÷3
x=220
答:超市购进220个大中国结。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系:大中国结的个数×3+20个=小中国结的个数,列方程解答。
30.【分析】阴影部分的面积等于梯形面积减去平行四边形的面积。利用梯形面积公式:S=(a+b)h÷2,平行四边形的面积:S=ah。
【解答】解:(22+34)×12÷2﹣1×12
=336﹣12
=324(平方米)
答:桃树的面积是324平方米。
【点评】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
31.【分析】根据“第二次比第一次多用了570元”,可以提炼这道题的等量关系是:第二次买衣服花的钱数﹣第一次买衣服花的钱数=570元,列方程解答。
【解答】解:设每套运动服x元。
32x﹣26x=570
6x=570
6x÷6=570÷6
x=95
答:每套运动服95元。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系:第二次买衣服花的钱数﹣第一次买衣服花的钱数=570元,列方程解答。
32.【分析】根据“一件上衣和一条裤子的总价钱是325元”,可以提炼这道题的等量关系是:一件上衣的钱数+一条裤子的钱数=325元,根据这个等量关系,列方程解答。
【解答】解:设一条裤子x元。
1.5x+x=325
2.5x=325
2.5x÷2.5=325÷2.5
x=130
130×1.5=195(元)
答:一件上衣195元,一条裤子150元。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系:一件上衣的钱数+一条裤子的钱数=325元,列方程解答。
33.【分析】(1)茄子地的面积是底为20m、高为15m的三角形的面积,根据三角形的面积公式S=ah÷2,求出茄子地的面积,然后再除以每棵茄子占地面积即可;
(2)白菜地的面积是底为30m、高为15m的三角形的面积,根据三角形的面积公式S=ah÷2,求出白菜地的面积,然后再乘平均每平方米能收白菜的质量即可。
【解答】解:(1)20×15÷2÷0.5
=150÷0.5
=300(棵)
答:这块茄子地可以种300棵茄子。
(2)30×15÷2×16
=225×16
=3600(千克)
答:这块白菜地能收3600千克白菜。
【点评】本题关键是根据三角形的面积公式分别求出茄子地和白菜地的面积,然后再根据乘除法的意义进行解答。
34.【分析】(1)根据统计表中的数据完成统计图;
(2)①观察统计图的直条,直条最高的就是人数最多的,直条最矮的就是人数最少的,求差即可求出多多少万人;
②用加法求出植树的总数,再除以5即可求出平均每年植树的棵树;
③观察统计图的直条走向,发现逐年增加,即植树的人数每年呈上升趋势。
【解答】解:(1)统计图如下:
(2)根据折线统计图完成下面问题。
①11﹣4=7(万人)
答:2019年参加义务植树的人数最多,有11万人,比最少的一年多7万人。
②4+5+7+8+11=35(万人)
35÷5=7(万人)
答:平均每年参加义务植树的人数有7万人。
③通过统计图可以看出,参加义务植树的人数一直呈上升趋势。
故答案为:2019,11,7;7;上升。
【点评】此题是考查条形统计图的意义及特征、从统计图中获取信息并根据所获取的信息进行有关计算是解题的关键。
一、填空题。(共33分)
1.(4分)在1、2、6、9、19、21、23、42、99这些数中,奇数有 ,质数有 ,合数有 ,既是偶数又是合数的数有 。
2.(2分)把一根5米长的铁丝平均截成6段,每段占全长的 ,每段长 米。
3.(2分)同时是2和3的倍数的数,最小的两位数是 ,最大的两位数是 .
4.(2分)粮店里新进批面粉,第一天卖出这批面粉的,第二天卖出这批面粉的,第三天卖出这批面粉的。三天一共卖出这批面粉的 ,还剩 。
5.(1分)泰山比海平面高1545米,记作+1545米;吐鲁番盆地比海平面低154米,记作 米。
6.(3分)在横线上填上最简分数。
65cm2= dm2 800克= 千克 50分= 时
7.(2分)在横线上填上合适的数。
86000平方米= 公顷;2.05平方千米= 公顷。
8.(4分)在横线上填上“>”“<”或“=”。
0.625 2
9.(4分)=0.35= ÷120==63÷ 。
10.(2分)两个相邻奇数的和是12,它们的最大公因数是 ,最小公倍数是 。
11.(3分) 个是;里面有 个,有 个。
12.(2分)两个完全一样的梯形拼成了一个平行四边形,平行四边形的面积是7.8平方厘米,高是3厘米,则一个梯形的面积是 平方厘米,梯形的上、下两底的和是 厘米。
13.(2分)的分数单位是 ,再加上 个这样的分数单位就是最小的质数。
二、选择题。(在括号内将正确答案的序号涂黑)(共5分)
14.(1分)与方程0.5x=3的解相同的是( )
A.0.6x=3 B.5x+6=12 C.0.5x+5=8 D.2x﹣6=12
15.(1分)下列说法正确的是( )
A.等底等高的三角形面积一定相等
B.平行四边形的面积是三角形面积的2倍
C.直角三角形只有1条高
D.两个面积相等的三角形一定能拼成一个平行四边形
16.(1分)一个三角形和一个平行四边形面积相等,底也相等。已知平行四边形的高是18厘米,三角形的一条高是
( )
A.9厘米 B.36厘米 C.18厘米 D.6厘米
17.(1分)已知两个数的最大公因数是6,最小公倍数是90,若一个数是18,则另一个数是( )
A.90 B.15 C.18 D.30
18.(1分)要使是假分数,是真分数,x应是( )
A.1 B.15 C.16 D.无法确定
三、判断题。(正确的涂“√”,错误的涂“×”)(共5分)
19.(1分)长方形是轴对称图形,有四条对称轴.
20.(1分)一个合数至少有3个因数
21.(1分)当长方形和平行四边形的周长相等时,面积也相等. .
22.(1分)两个质数的乘积一定是合数. .
23.(1分)如果一个数是6的倍数,那么它一定是2和3的倍数.
四、计算。(共21分)
24.(5分)直接写得数。
+= ﹣= += ﹣=
+= ﹣= += ﹣=
﹣= +=
25.(10分)计算。
1﹣﹣ ﹣+
+﹣ ++
26.(6分)解方程。
3.8x+5.2x=52.2 8.5+1.6x=12.5 35.6﹣x=18.9
五、画一画。(4分)
27.(4分)画一画。
(1)画出左图的另一半,使它成为一个轴对称图形。
(2)将右面绕O点逆时针旋转90°,画出旋转后的图形。
六、看图列方程,并求解。(共6分)
28.(6分)看图列方程,并求解。
七、解决问题。(共26分)
29.(4分)利民超市购进680个小中国结,比购进的大中国结的3倍多20个。超市购进多少个大中国结?(用方程解答)
30.(4分)王伯伯在一块梯形果园里修了一条底长为1 米、高为12米的平行四边形小路(如图)。阴影部分的果园种桃树,求桃树的面积是多少平方米?
31.(4分)王老师第一次到体育用品店买了26套运动服,第二次又买了同样的32套运动服,第二次比第一次多用了570元。每套运动服多少元?(用方程解答)
32.(4分)一件上衣和一条裤子的总价钱是325元,一件上衣的价钱是一条裤子的1.5倍。一件上衣和一条裤子分别是多少元?(用方程解答)
33.(4分)如图,菜园里有两块空地,计划种茄子和白菜。
(1)如果每棵茄子占地0.5平方米,这块茄子地可以种多少棵茄子?
(2)如果平均每平方米能收16千克白菜,这块白菜地能收多少千克白菜?
34.(6分)下面是某市2015~2019年参加义务植树活动人数统计表。
年份(年) 2015 2016 2017 2018 2019
人数(万人) 4 5 7 8 11
(1)根据上表中数据,完成下面折线统计图。
(2)根据折线统计图完成下面问题。
① 年参加义务植树的人数最多,有 万人,比最少的一年多 万人。
②平均每年参加义务植树的人数有 万人。
③通过统计图可以看出,参加义务植树的人数一直呈 趋势。
2020-2021学年山东省烟台市开发区四年级(下)期末数学试卷
参考答案与试题解析
一、填空题。(共33分)
1.【分析】偶数:是2的倍数的数叫作偶数;
奇数:不是2的倍数的数叫作奇数。
质数:一个数只有1和它本身两个因数,这个数叫作质数。
合数:指自然数中除了能被1和本身整除外,还能被其他的数整除的数。
“0”“1”既不是质数也不是合数。
【解答】解:在1、2、6、9、19、21、23、42、99这些数中,奇数有1、9、19、21、23、99,质数有2、18、23,合数有6、9、21、42、99,既是偶数又是合数的数有6、42。
故答案为:1、9、19、21、23、99;2、18、23;6、9、21、42、99;6、42。
【点评】此题主要考查了质数、合数、奇数、偶数的定义,要熟练掌握。
2.【分析】根据题意,把5米长的铁丝看作单位“1”,平均分成6段,每段就占6段的,求每段长多少米,利用全长除以段数即可。
【解答】解:1÷6=
5(米)
答:每段占全长的,每段长米。
故答案为:,。
【点评】此题重在区分分数在具体的题目中的区别:有些表示是某些量的几分之几,有些表示具体的数,做到正确区分,选择合适的解题方法。
3.【分析】同时是2和3的倍数的数一定是6的倍数,如6、12、18…,最小的两位数是12,因此得解;因为2和3最小公倍数是6,所以求既是3的倍数、又是2的倍数的最大两位数,即求100以内的6的最大倍数.
【解答】解:同时是2和3的倍数的数,最小的两位数是12,最大的两位数是96.
故答案为:12,96.
【点评】此题考查了找一个数的倍数的方法,明白同时是2和3的倍数,就是求6的倍数是解决此题的关键.
4.【分析】把这批面粉的总量看成单位“1”,第一天卖出这批面粉的,第二天卖出这批面粉的,第三天卖出这批面粉的,把这三个分率相加,即可求出一共卖出了这批面粉的几分之几;用单位“1”减去三天一共卖出这批面粉的分率,即可得剩下的。
【解答】解:
=
=
1﹣
答:三天一共卖出这批面粉的,还剩。
故答案为:,。
【点评】解决本题关键是理解把这批面粉的总量看成单位“1”,再根据分数加减法的意义求解。
5.【分析】用正负数表示意义相反的两种量:高于海平面记作正,则低于海平面就记作负。由此得解。
【解答】解:泰山比海平面高1545米,记作+1545米;吐鲁番盆地比海平面低154米,记作﹣154米。
故答案为:﹣154。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
6.【分析】低级单位平方厘米化高级单位平方分米除以进率100;
低级单位克化高级单位千克除以进率1000;
低级单位分化高级单位时除以进率60。
【解答】解:
65cm2=dm2 800克=千克 50分=时
故答案为:,,。
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。结果用分数表示时,通常化成最简分数。
7.【分析】根据1公顷=10000平方米,1平方千米=100公顷,解答此题即可。
【解答】解:86000平方米=8.6公顷;2.05平方千米=205公顷。
故答案为:8.6;205。
【点评】熟练掌握面积单位的换算,是解答此题的关键。
8.【分析】两个分数分别与1作差,差越小的原分数越大;先通分再比较大小;把分数化成小数,再比较大小;把带分数化成假分数,再根据同分母分数比较大小的方法进行比较。
【解答】解:因为1﹣=
1﹣=
因为
所以
因为=
所以<
因为=0.625
所以0.625=
因为2=<所以2<> <
0.625= 2<
故答案为:>,<,=,<。
【点评】熟练掌握用作差法比较分数大小的方法、异分母分数比较大小的方法、分数化成小数的方法以及带分数化成假分数的方法是解题的关键。
9.【分析】把0.35化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;都乘10就是;根据分数与除法的关系,=7÷20,再根据商不变的性质被除数、除数都乘6就是42÷120;都乘9就是63÷180。
【解答】解:=0.35=42÷120==63÷180。
故答案为:28,42,200,180。
【点评】此题主要是考查除法、小数、分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
10.【分析】先根据两个相邻奇数的和是12,求得这两个奇数为5和7,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积。
【解答】解:两个相邻奇数的和是12,则两个数为5和7
5和7的最大公因数是1,最小公倍数是5×7=35
故答案为:1,35。
【点评】考查了求几个数的最大公因数的方法与最小公倍数的方法:两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积。
11.【分析】已知一个数的几分之几是多少,求这个数用除法计算;再根据包含除法的意义,计算第二、第三小题。
【解答】解:
=
=6
=
=5
=
=10
答:6个是;里面有5个,有10个。
故答案为:6;5;10。
【点评】本题解题关键是根据分数除法的意义列出算式,再根据分数除法的计算法则,算出结果。
12.【分析】两个完全一样的梯形可以拼成一个平行四边形.这个平行四边形的面积是原来两个梯形面积的和,即为每个梯形面积的2倍,由“两个完全一样的梯形拼成的平行四边形面积是7.8平方厘米”可以求出一个梯形的面积,又因梯形的高已知,于是利用梯形的面积乘2,再除以梯形的高,即可求出上下底的和。
【解答】解:7.8÷2=3.9(平方厘米)
3.9×2÷3
=7.8÷3
=2.6(厘米)
答:一个梯形的面积是3.9平方厘米,梯形的上、下两底的和2.6厘米。
故答案为:3.9,2.6。
【点评】此题主要考查梯形的面积公式的推导过程,要注意两个完全一样的平面图形拼成一个图形,其面积就等于原图形的面积的2倍。
13.【分析】将单位“1”平均分成若干份,表示其中这样一份的数叫分数单位.由此可知,的分数单位是;最小的质数为2,2﹣=,里面有11个,所以再加上11个这样的分数单位就是最小的质数。
【解答】解:根据分数单位的意义可知,
的分数单位是;
2﹣=
所以再加上11个这样的分数单位就是最小的质数。
故答案为:,11。
【点评】一个分数的分母是几,其分数单位就是几分之一,分子是几,其就含有几个分数单位(带分数除外)。
二、选择题。(在括号内将正确答案的序号涂黑)(共5分)
14.【分析】先根据等式的基本性质,方程0.5x=3的两边同时除以0.5,求出x的值,再把x的值分别代入各选项中的方程,能使方程左边等于右边的就是与方程0.5x=3的解相同的方程。
【解答】解:0.5x=3
0.5x÷0.5=3÷0.5
x=6
A.把x=6代入方程0.6x=3,得:0.6×6=3.6≠方程右边,所以x=6不是该方程的解;
B.把x=6代入方程5x+6=12,得:5×6+6=36≠12,所以x=6不是该方程的解;
C.把x=6代入方程0.5x+5=8,得:0.5×6+5=8=方程右边,所以x=6是该方程的解;
D.把x=6代入方程2x﹣6=12,得:2×6﹣6=6≠12,所以x=6不是该方程的解。
故选:C。
【点评】熟练掌握方程的检验方法是解题的关键。
15.【分析】根据三角形的面积=底×高÷2可知:等底等高的三角形面积一定相等;等底等高的平行四边形的面积是三角形面积的2倍;任何三角形都有3条高;两个形状和大小都相同的三角形一定能拼成一个平行四边形,据此解答即可。
【解答】解:A.根据三角形的面积=底×高÷2可知:等底等高的三角形面积一定相等,题干说法正确;
B.等底等高的平行四边形的面积是三角形面积的2倍,题干说法是错误的;
C.任何三角形都有3条高,题干说法是错误的;
D.两个形状和大小都相同的三角形一定能拼成一个平行四边形,题干说法是错误的。
故选:A。
【点评】熟练掌握三角形和平行四边形的面积公式,三角形高的定义和画法,是解答此题的关键。
16.【分析】根据一个三角形和一个平行四边形面积相等,底也相等,那么三角形的高是平行四边形的高的2倍,据此解答即可。
【解答】解:18×2=36(厘米)
答:三角形的一条高是36厘米。
故选:B。
【点评】根据面积相等,底也相等的三角形和平行四边形底的倍数关系,解答此题即可。
17.【分析】用最小公倍数90除以已知数字18,得到所求数字的独有质因数的积,然后乘公有质因数的积(最大公约数6),即可得解.
【解答】解:90÷18=5
5×6=30
答:另一个数是30.
故选:D.
【点评】灵活应用“求最大公约数也就是这几个数的公有质因数的连乘积,最小公倍数是共有质因数与独有质因数的连乘积”的逆运算来求另一个数.
18.【分析】假分数是分子大于或等于1的分数,真分数小于1,分子比分母小,据此解答。
【解答】解:若是假分数,那么x可以等于分母15或大于15;
若是真分数,那么分子x必须小于分母16。
根据以上分析,x=15符合题意。
故选:B。
【点评】本题考查了真分数和假分数的定义。
三、判断题。(正确的涂“√”,错误的涂“×”)(共5分)
19.【分析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴,据此即可进行判断.
【解答】解:长方形是轴对称图形,有2条对称轴,故原题说法错误;
故答案为:×.
【点评】解答此题的主要依据是:轴对称图形的意义及特征.
20.【分析】自然数中,除了1和它本身外,还有别的因数的数为合数.由此可知,合数除了1和它本身外,至少还要有一个因数,即至少有3个因数,如9有1,9,3三个因数.
【解答】解:根据合数的意义可知,
合数除了1和它本身外,至少还要有一个因数,即至少有3个因数.
所以一个合数至少有3个因数说法正确.
故答案为:√.
【点评】根据合数的意义进行确定是完成本题的关键.
21.【分析】当长方形和平行四边形的周长相等时,则它们的边长可能相等,但高不一定相等,所以面积就不一定相等.
【解答】解:因为当长方形和平行四边形的周长相等时,
则它们的边长可能相等,但高不一定相等,所以面积也就不一定相等;
故答案为:×.
【点评】此题主要考查长方形和平行四边形的周长及面积计算公式.
22.【分析】根据质数与合数的定义即可做出判断.
【解答】解:质数只有两个约数,合数至少有三个约数,两个质数的乘积至少有四个约数,如2×3=6,6的约数有1、2、3、6;3×5=15,15的约数有1、3、5、15;2×5=10,10的约数有1、2、5、10.等等.
答:两个质数的乘积一定是合数.
故此题正确.
【点评】此题考查目的是对质数、合数定义的理解.
23.【分析】把6分解因数发现,2和3都是6的因数,所以一个数是6的倍数,那么它一定是2和3的倍数.
【解答】解:6=2×3,
6是2和3的倍数,所以一个数是6的倍数,那么它一定是2和3的倍数.
原题说法正确.
故答案为:√.
【点评】此题主要考查了因数和倍数的意义,注意知识的灵活运用.
四、计算。(共21分)
24.【分析】根据同分母分数相加(减),分子进行相加(减)得数作分子,分母不变,计算即可,注意结果化到最简。
【解答】解:
+= ﹣= += ﹣=
+=1 ﹣= += ﹣=
﹣= +=
【点评】考查了同分母分数的加法和减法运算,关键是熟练掌握计算法则正确进行计算。
25.【分析】根据同分母分数相加(减),分子进行相加(减)得数作分子,分母不变,计算即可,注意结果要化到最简。
【解答】解:1﹣﹣
=
=
﹣+
=
=
+﹣
=
=
++
=
=
【点评】考查了同分母分数的加法和减法运算,关键是熟练掌握计算法则正确进行计算。
26.【分析】(1)先把方程左边化简为9x,两边再同时除以9;
(2)方程两边同时减去8.5,两边再同时除以1.6;
(3)方程两边同时加上x,两边再同时减去18.9。
【解答】解:(1)3.8x+5.2x=52.2
9x=52.2
9x÷9=52.2÷9
x=5.8
(2)8.5+1.6x=12.5
8.5+1.6x﹣8.5=12.5﹣8.5
1.6x=4
1.6x÷1.6=4÷1.6
x=2.5
(3)35.6﹣x=18.9
35.6﹣x+x=18.9+x
18.9+x﹣18.9=35.6﹣18.9
x=16.7
【点评】熟练掌握等式的基本性质是解题的关键。
五、画一画。(4分)
27.【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出左半图的关键对称点,依次连接即可。
(2)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【解答】解:根据题意画图如下:
【点评】作旋转一定度数后的图形、作轴对称图形,对应点(对称点)位置的确定是关键。
六、看图列方程,并求解。(共6分)
28.【分析】(1)根据图意,题中的等量关系是:绳子的总长度﹣截去的米数=还剩下的米数,根据这个等量关系,列方程解答。
(2)从图上可得:柳树的棵数比杨树的3倍少67棵,所以它们之间的数量关系为:杨树棵数×3﹣67=柳树的棵树,根据这个等量关系,列方程解答即可。
【解答】解:(1)x﹣130=120
x﹣130+130=120+130
x=250
答:绳长250米。
(2)3x﹣67=269
3x﹣67+67=269+67
3x=336
3x÷3=336÷3
x=112
答:杨树有112棵。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系。
七、解决问题。(共26分)
29.【分析】根据“小中国结比购进的大中国结的3倍多20个”,可以提炼这道题的等量关系是:大中国结的个数×3+20个=小中国结的个数,根据这个等量关系列方程解答。
【解答】解:设超市购进x个大中国结。
3x+20=680
3x+20﹣20=680﹣20
3x=660
3x÷3=660÷3
x=220
答:超市购进220个大中国结。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系:大中国结的个数×3+20个=小中国结的个数,列方程解答。
30.【分析】阴影部分的面积等于梯形面积减去平行四边形的面积。利用梯形面积公式:S=(a+b)h÷2,平行四边形的面积:S=ah。
【解答】解:(22+34)×12÷2﹣1×12
=336﹣12
=324(平方米)
答:桃树的面积是324平方米。
【点评】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
31.【分析】根据“第二次比第一次多用了570元”,可以提炼这道题的等量关系是:第二次买衣服花的钱数﹣第一次买衣服花的钱数=570元,列方程解答。
【解答】解:设每套运动服x元。
32x﹣26x=570
6x=570
6x÷6=570÷6
x=95
答:每套运动服95元。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系:第二次买衣服花的钱数﹣第一次买衣服花的钱数=570元,列方程解答。
32.【分析】根据“一件上衣和一条裤子的总价钱是325元”,可以提炼这道题的等量关系是:一件上衣的钱数+一条裤子的钱数=325元,根据这个等量关系,列方程解答。
【解答】解:设一条裤子x元。
1.5x+x=325
2.5x=325
2.5x÷2.5=325÷2.5
x=130
130×1.5=195(元)
答:一件上衣195元,一条裤子150元。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系:一件上衣的钱数+一条裤子的钱数=325元,列方程解答。
33.【分析】(1)茄子地的面积是底为20m、高为15m的三角形的面积,根据三角形的面积公式S=ah÷2,求出茄子地的面积,然后再除以每棵茄子占地面积即可;
(2)白菜地的面积是底为30m、高为15m的三角形的面积,根据三角形的面积公式S=ah÷2,求出白菜地的面积,然后再乘平均每平方米能收白菜的质量即可。
【解答】解:(1)20×15÷2÷0.5
=150÷0.5
=300(棵)
答:这块茄子地可以种300棵茄子。
(2)30×15÷2×16
=225×16
=3600(千克)
答:这块白菜地能收3600千克白菜。
【点评】本题关键是根据三角形的面积公式分别求出茄子地和白菜地的面积,然后再根据乘除法的意义进行解答。
34.【分析】(1)根据统计表中的数据完成统计图;
(2)①观察统计图的直条,直条最高的就是人数最多的,直条最矮的就是人数最少的,求差即可求出多多少万人;
②用加法求出植树的总数,再除以5即可求出平均每年植树的棵树;
③观察统计图的直条走向,发现逐年增加,即植树的人数每年呈上升趋势。
【解答】解:(1)统计图如下:
(2)根据折线统计图完成下面问题。
①11﹣4=7(万人)
答:2019年参加义务植树的人数最多,有11万人,比最少的一年多7万人。
②4+5+7+8+11=35(万人)
35÷5=7(万人)
答:平均每年参加义务植树的人数有7万人。
③通过统计图可以看出,参加义务植树的人数一直呈上升趋势。
故答案为:2019,11,7;7;上升。
【点评】此题是考查条形统计图的意义及特征、从统计图中获取信息并根据所获取的信息进行有关计算是解题的关键。
同课章节目录
