人教版八年级数学上册12.3角的平分线的性质课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 06:27:03 | ||
图片预览




文档简介
(共18张PPT)
八年级—人教版—数学—第十二章
角的平分线的性质(2)
学习目标
1.探索并证明角的平分线的判定定理;
2.会应用角的平分线的判定进行简单的计算或证明.
学习重难点
学习重点:探索并证明角的平分线的判定定理;
学习难点:综合应用角的平分线的性质与判定进行计算或者证明.
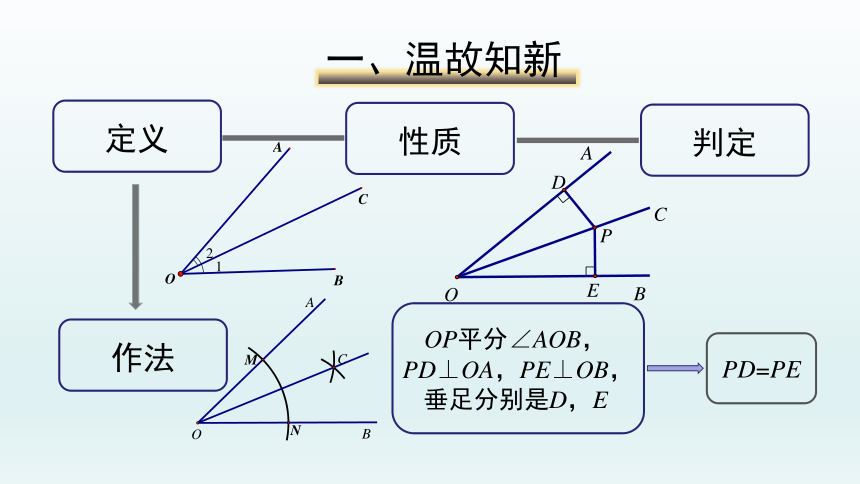
定义
作法
性质
判定
OP平分∠AOB,
PD⊥OA,PE⊥OB,
垂足分别是D,E
PD=PE
一、温故知新
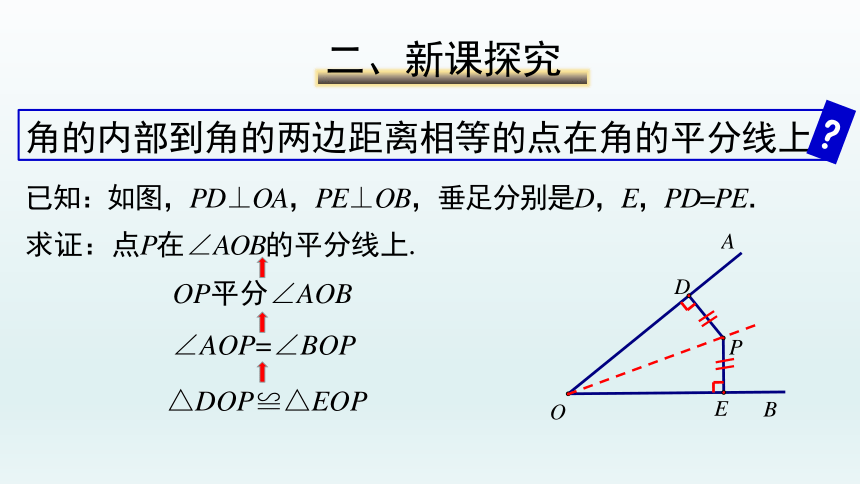
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE.
求证:点P在∠AOB的平分线上.
角的内部到角的两边距离相等的点在角的平分线上.
?
二、新课探究
OP平分∠AOB
∠AOP=∠BOP
△DOP≌△EOP
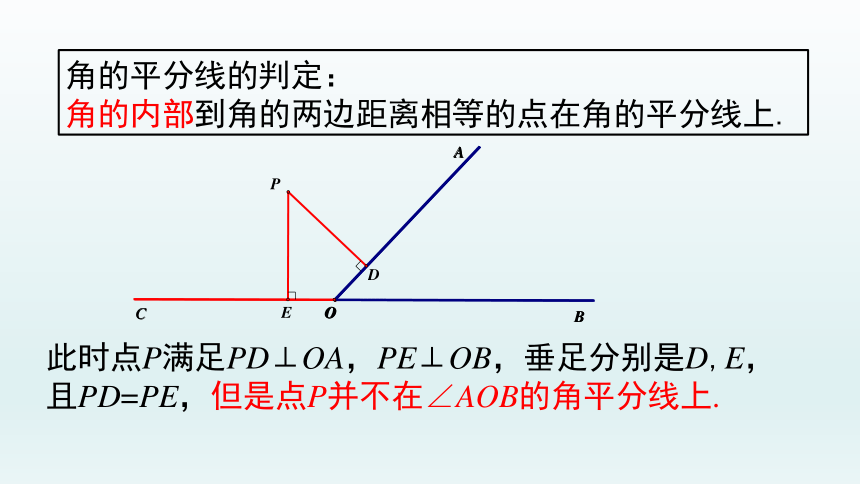
此时点P满足PD⊥OA,PE⊥OB,垂足分别是D,E,且PD=PE,但是点P并不在∠AOB的角平分线上.
角的平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
证明:
作射线OP.
∴点P在∠AOB 的平分线上.
在Rt△PDO和Rt△PEO 中,
OP=OP,
PD=PE ,
∵PD⊥OA,PE⊥OB ,
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP.
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,
PD =PE.
求证:点P在∠AOB的平分线上.
角的平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
几何语言描述:
如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE,
∴点P在∠AOB的平分线上.
判断以下说法正确吗?
(1)如图1,若QM =QN,则OQ 平分∠AOB;( )
判断以下说法正确吗?
(2)如图2,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线; ( )
判断以下说法正确吗?
(3)如图3,若QM⊥OA 于M,QN⊥OB 于N,且QM=QN,则点Q在∠AOB 的平分线上.( )
双垂直+等线段
如图3,若QM⊥OA 于M,QN⊥OB 于N,且OM=ON,
∴点O在∠MQN的平分线上.
例1:如图,要在S区建一个集贸市场,使它到铁路、公路的距离相等, 并且离公路与铁路交叉处500m,这个集贸市场应建于何处(在图中标出它的位置,比例尺为1︰20000)?
D
C
S
O
A
B
三、例题讲解
500m=50000cm
设图中集贸市场与点O之间距离为xcm
例1:如图,要在S区建一个集贸市场,使它到铁路、公路的距离相等, 并且离公路与铁路交叉处500m,这个集贸市场应建于何处(在图中标出它的位置,比例尺为1︰20000)?
D
C
S
O
A
B
三、例题讲解
解:做夹角∠AOB的角平分线OC.
设与交点O的距离为xcm,
,解得x=2.5cm,
∴在图上取OD=2.5cm,则点D为集贸市场的位置.
D
E
F
A
B
C
P
N
M
例2:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
BP平分∠ABC,
PD⊥AB,PE⊥BC,
垂足是D,E,
PD=PE
CP平分∠ACB,
PE⊥BC,PF⊥AC ,垂足是E,F,
PE=PF
PD=PE=PF
D
E
F
A
B
C
P
N
M
例2:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵ BM是△ABC的角平分线,
点P在BM上,
∴ PD=PE .
同理 PE=PF .
∴ PD=PE=PF .
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
例2:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
∵PD⊥AB,PF⊥AC,垂足分别是D,F, PD=PF,
小结:三角形三个内角的平分线交于一点,而且这个点到三边的距离相等.
∴点P在∠BAC的角平分线上.
定义
性质
判定
四、知识小结
如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE .
点P在∠AOB的平分线上.
角的平分线的判定
五、课后作业
课本P50练习第1题
八年级—人教版—数学—第十二章
角的平分线的性质(2)
学习目标
1.探索并证明角的平分线的判定定理;
2.会应用角的平分线的判定进行简单的计算或证明.
学习重难点
学习重点:探索并证明角的平分线的判定定理;
学习难点:综合应用角的平分线的性质与判定进行计算或者证明.
定义
作法
性质
判定
OP平分∠AOB,
PD⊥OA,PE⊥OB,
垂足分别是D,E
PD=PE
一、温故知新
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE.
求证:点P在∠AOB的平分线上.
角的内部到角的两边距离相等的点在角的平分线上.
?
二、新课探究
OP平分∠AOB
∠AOP=∠BOP
△DOP≌△EOP
此时点P满足PD⊥OA,PE⊥OB,垂足分别是D,E,且PD=PE,但是点P并不在∠AOB的角平分线上.
角的平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
证明:
作射线OP.
∴点P在∠AOB 的平分线上.
在Rt△PDO和Rt△PEO 中,
OP=OP,
PD=PE ,
∵PD⊥OA,PE⊥OB ,
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP.
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,
PD =PE.
求证:点P在∠AOB的平分线上.
角的平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
几何语言描述:
如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE,
∴点P在∠AOB的平分线上.
判断以下说法正确吗?
(1)如图1,若QM =QN,则OQ 平分∠AOB;( )
判断以下说法正确吗?
(2)如图2,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线; ( )
判断以下说法正确吗?
(3)如图3,若QM⊥OA 于M,QN⊥OB 于N,且QM=QN,则点Q在∠AOB 的平分线上.( )
双垂直+等线段
如图3,若QM⊥OA 于M,QN⊥OB 于N,且OM=ON,
∴点O在∠MQN的平分线上.
例1:如图,要在S区建一个集贸市场,使它到铁路、公路的距离相等, 并且离公路与铁路交叉处500m,这个集贸市场应建于何处(在图中标出它的位置,比例尺为1︰20000)?
D
C
S
O
A
B
三、例题讲解
500m=50000cm
设图中集贸市场与点O之间距离为xcm
例1:如图,要在S区建一个集贸市场,使它到铁路、公路的距离相等, 并且离公路与铁路交叉处500m,这个集贸市场应建于何处(在图中标出它的位置,比例尺为1︰20000)?
D
C
S
O
A
B
三、例题讲解
解:做夹角∠AOB的角平分线OC.
设与交点O的距离为xcm,
,解得x=2.5cm,
∴在图上取OD=2.5cm,则点D为集贸市场的位置.
D
E
F
A
B
C
P
N
M
例2:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
BP平分∠ABC,
PD⊥AB,PE⊥BC,
垂足是D,E,
PD=PE
CP平分∠ACB,
PE⊥BC,PF⊥AC ,垂足是E,F,
PE=PF
PD=PE=PF
D
E
F
A
B
C
P
N
M
例2:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵ BM是△ABC的角平分线,
点P在BM上,
∴ PD=PE .
同理 PE=PF .
∴ PD=PE=PF .
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
例2:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等.
∵PD⊥AB,PF⊥AC,垂足分别是D,F, PD=PF,
小结:三角形三个内角的平分线交于一点,而且这个点到三边的距离相等.
∴点P在∠BAC的角平分线上.
定义
性质
判定
四、知识小结
如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE .
点P在∠AOB的平分线上.
角的平分线的判定
五、课后作业
课本P50练习第1题
