沪科版八年级数学上册13.2命题与证明(四)三角形的外角教案
文档属性
| 名称 | 沪科版八年级数学上册13.2命题与证明(四)三角形的外角教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 08:15:56 | ||
图片预览

文档简介
13.2命题与证明(四)
三角形的外角
教学目标
知识与技能
1、理解三角形的外角的概念;
2、掌握三角形外角的性质,能利用三角形外角的性质解决问题。
过程与方法
在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯
情感、态度与价值观
体会数学与现实生活的联系,增强克服困难的勇气和信心
重点:理解并掌握三角形外角的性质
难点:三角形的外角的性质论证过程及运用于简单的实际问题的解决
教学过程
一、导入新课: 前面我们已经学习了三角形的内角, 现在老师给出一个三角形,同学们找出的它的内角是什么?
A
B C
现在老师把BC边延长到D,又新形成了一个角 ∠ACD,那
尝试活动,探索新知
<一>、 三角形的外角定义: 三角形的一边和另一边的延长线组成的角叫做三角形的外角。
从外角的定义上看外角有如下特点:
(1)顶点是三角形的一个顶点
(2) 一边是三角形的一条边
(3) 另一边是三角形某条边的延长线
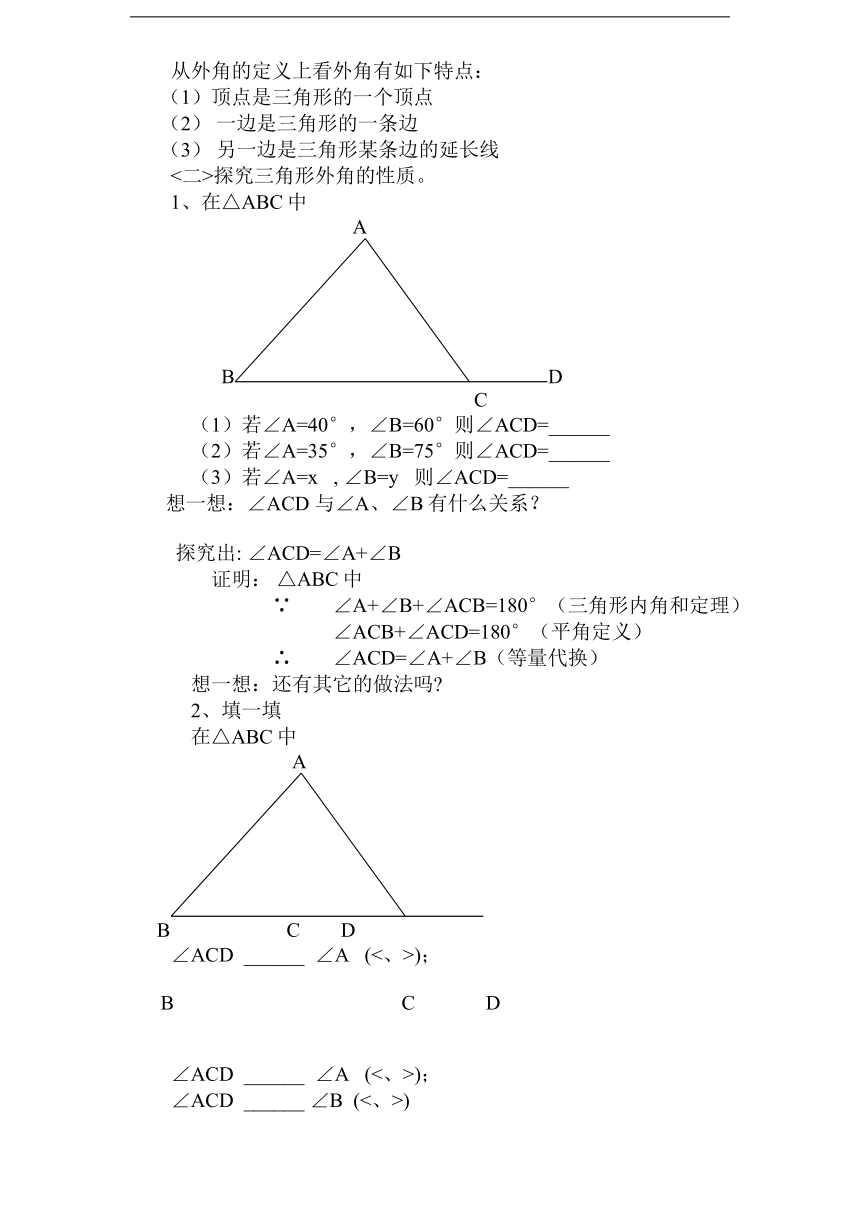
<二>探究三角形外角的性质。
1、在△ABC中
A
BD
C
(1)若∠A=40°,∠B=60°则∠ACD=______
(2)若∠A=35°,∠B=75°则∠ACD=______
(3)若∠A=x , ∠B=y 则∠ACD=______
想一想:∠ACD 与∠A、∠B有什么关系?
探究出: ∠ACD=∠A+∠B
证明: △ABC中
∵ ∠A+∠B+∠ACB=180°(三角形内角和定理)
∠ACB+∠ACD=180°(平角定义)
∴ ∠ACD=∠A+∠B(等量代换)
想一想:还有其它的做法吗
2、填一填
在△ABC中
A
B C D
∠ACD ______ ∠A (<、>);
B C D
∠ACD ______ ∠A (<、>);
∠ACD ______ ∠B (<、>)
通过探究得出了多边形外角的性质
(1)三角形的一个外角等于与它不相邻的两个内角的和。
(2) 三角形的一个外角大于与它不相邻的任何一个内角。
<三>、学以致用: 运用三角形外角的性质来做题
如图:∠1、∠2、∠3是△ABC的三个外角,他们的和是多少?
解: ∵ ∠1=∠ABC+∠ACB
∠2=∠ACB+ ∠BAC
∠3=∠ABC+ ∠BAC
(三角形的一个外角等于与它不相邻的两个内角的和)
∴ ∠1+∠2+∠3=2(∠ABC+∠ACB+∠BAC) (等式的基本性质)
∵ ∠ABC+∠ACB+∠BAC=180°(三角形内角和定理)
∴ ∠1+∠2+∠3=360°
三、当堂检测
把图中∠1、 ∠2、 ∠3按从大到小的顺序排列,并说明理由。
四、课时小结:
1、三角形的一个外角等于与它不相邻的两个内角的和。
2、三角形的一个外角大于任何一个与它不相邻的内角。
五、布置作业
课堂作业:习题13.2第4题,第9题.
家庭作业:1、基础训练13.2(4)
2、预学下一节内容。
六、 板书设计
13.2三角形的外角 一、三角形外角的定义 三角形的一边和另一边的延长线组成的角叫做三角形的外角。 二、三角形外角的性质 1、三角形的一个外角等于与它不相邻的两个内角的和。 2、 三角形的一个外角大于与它不相邻的任何一个内角 三、例题
三角形的外角
教学目标
知识与技能
1、理解三角形的外角的概念;
2、掌握三角形外角的性质,能利用三角形外角的性质解决问题。
过程与方法
在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯
情感、态度与价值观
体会数学与现实生活的联系,增强克服困难的勇气和信心
重点:理解并掌握三角形外角的性质
难点:三角形的外角的性质论证过程及运用于简单的实际问题的解决
教学过程
一、导入新课: 前面我们已经学习了三角形的内角, 现在老师给出一个三角形,同学们找出的它的内角是什么?
A
B C
现在老师把BC边延长到D,又新形成了一个角 ∠ACD,那
尝试活动,探索新知
<一>、 三角形的外角定义: 三角形的一边和另一边的延长线组成的角叫做三角形的外角。
从外角的定义上看外角有如下特点:
(1)顶点是三角形的一个顶点
(2) 一边是三角形的一条边
(3) 另一边是三角形某条边的延长线
<二>探究三角形外角的性质。
1、在△ABC中
A
BD
C
(1)若∠A=40°,∠B=60°则∠ACD=______
(2)若∠A=35°,∠B=75°则∠ACD=______
(3)若∠A=x , ∠B=y 则∠ACD=______
想一想:∠ACD 与∠A、∠B有什么关系?
探究出: ∠ACD=∠A+∠B
证明: △ABC中
∵ ∠A+∠B+∠ACB=180°(三角形内角和定理)
∠ACB+∠ACD=180°(平角定义)
∴ ∠ACD=∠A+∠B(等量代换)
想一想:还有其它的做法吗
2、填一填
在△ABC中
A
B C D
∠ACD ______ ∠A (<、>);
B C D
∠ACD ______ ∠A (<、>);
∠ACD ______ ∠B (<、>)
通过探究得出了多边形外角的性质
(1)三角形的一个外角等于与它不相邻的两个内角的和。
(2) 三角形的一个外角大于与它不相邻的任何一个内角。
<三>、学以致用: 运用三角形外角的性质来做题
如图:∠1、∠2、∠3是△ABC的三个外角,他们的和是多少?
解: ∵ ∠1=∠ABC+∠ACB
∠2=∠ACB+ ∠BAC
∠3=∠ABC+ ∠BAC
(三角形的一个外角等于与它不相邻的两个内角的和)
∴ ∠1+∠2+∠3=2(∠ABC+∠ACB+∠BAC) (等式的基本性质)
∵ ∠ABC+∠ACB+∠BAC=180°(三角形内角和定理)
∴ ∠1+∠2+∠3=360°
三、当堂检测
把图中∠1、 ∠2、 ∠3按从大到小的顺序排列,并说明理由。
四、课时小结:
1、三角形的一个外角等于与它不相邻的两个内角的和。
2、三角形的一个外角大于任何一个与它不相邻的内角。
五、布置作业
课堂作业:习题13.2第4题,第9题.
家庭作业:1、基础训练13.2(4)
2、预学下一节内容。
六、 板书设计
13.2三角形的外角 一、三角形外角的定义 三角形的一边和另一边的延长线组成的角叫做三角形的外角。 二、三角形外角的性质 1、三角形的一个外角等于与它不相邻的两个内角的和。 2、 三角形的一个外角大于与它不相邻的任何一个内角 三、例题
