沪科版八年级数学上册12.2 《 一次函数解决问题》教学设计(表格式)
文档属性
| 名称 | 沪科版八年级数学上册12.2 《 一次函数解决问题》教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 18.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览

文档简介
一次函数解决问题
沪科版八年级上册《第12章 一次函数》
教学目标
(1)掌握并运用一次函数的图象和性质,体会数形结合思想和建立函数模型研究数学问题的基本方法.
(2)通过对实际问题图象的分析,进一步加深对一次函数性质的理解.
(3)能够从实际问题中抽象出一次函数关系,并运用一次函数及其性质解决实际问题,发展学生的应用意识.
教学重难点 :理解实际问题中一次函数的模型,并利用所学知识解决问题.
教学过程设计
教学过程设计
问题与情境 师生活动 设计意图
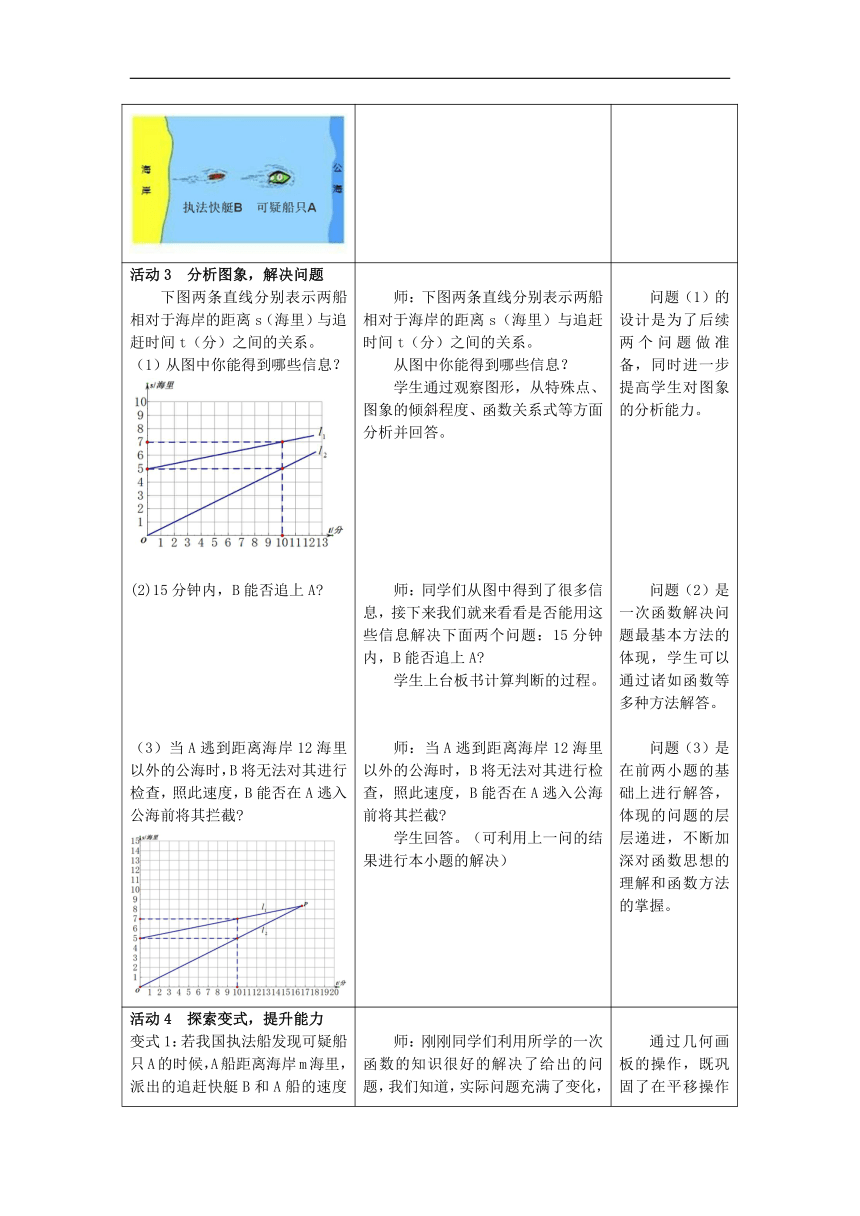
活动1 复习回顾 师:在前面的学习中,我们已经了解了一次函数的定义和性质,我们知道,一次函数的一般形式是。。。(生答)对于一次函数y=0.2x+5,大家能说出k和b在图中的意义吗?学生回答。师:加入了一次函数y=0.5x之后,两个图象的交点坐标大家会求吗?请动手试一试。学生求解出交点坐标。师追问:交点坐标的意义是什么?什么时候y1>y2,什么时候y1活动2 观看视频,展示问题1、观看视频2、给出问题问题:我国执法船接到情报,近海处有一可疑船只A正向公海方向行驶,执法船迅速派出快艇B追赶。 师:数学来源于生活,应用于生活。下面我们就一起来看看一次函数在具体问题中的应用,请同学们先看视频。学生观看中国渔政执法视频。师展示问题。 通过中国渔政执法视频的展示,体现数学来源于生活,同时抒发爱国情怀,引导学生进入数学学习。
活动3 分析图象,解决问题下图两条直线分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。(1)从图中你能得到哪些信息?(2)15分钟内,B能否追上A (3)当A逃到距离海岸12海里以外的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截 师:下图两条直线分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。从图中你能得到哪些信息?学生通过观察图形,从特殊点、图象的倾斜程度、函数关系式等方面分析并回答。师:同学们从图中得到了很多信息,接下来我们就来看看是否能用这些信息解决下面两个问题:15分钟内,B能否追上A 学生上台板书计算判断的过程。师:当A逃到距离海岸12海里以外的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截 学生回答。(可利用上一问的结果进行本小题的解决) 问题(1)的设计是为了后续两个问题做准备,同时进一步提高学生对图象的分析能力。问题(2)是一次函数解决问题最基本方法的体现,学生可以通过诸如函数等多种方法解答。问题(3)是在前两小题的基础上进行解答,体现的问题的层层递进,不断加深对函数思想的理解和函数方法的掌握。
活动4 探索变式,提升能力变式1:若我国执法船发现可疑船只A的时候,A船距离海岸m海里,派出的追赶快艇B和A船的速度不变,要保证B还能在A进入公海前将其拦截,则m的最大值是多少? 变式2:若A将速度提高至Va,B要保证A逃到公海前将其拦截,B也将速度提高至Vb,那么Va和Vb需要满足什么条件 师:刚刚同学们利用所学的一次函数的知识很好的解决了给出的问题,我们知道,实际问题充满了变化,若将l1向上平移,这样的操作从实际意义来看,什么发生了改变,什么没有改变?学生感知后,思考回答。师追问:若我国执法船发现可疑船只A的时候,A船距离海岸m海里,派出的追赶快艇B和A船的速度不变,要保证B还能在A进入公海前将其拦截,则m的最大值是多少?先由一名学生上台操作几何画板,找到m最大值的情况。学生再计算后回答。师操作:拉动交点P的位置。师:这样的操作从实际意义来看,什么发生了改变,什么没有改变?学生回答。师追问:我们知道,在被发现时间固定的情况下,A船想要逃跑,必须加速。但我们的执法B船肯定会圆满完成任务,顺利拦截。若A将速度提高至Va,B要保证A逃到公海前将其拦截,B也将速度提高至Vb,那么Va和Vb需要满足什么条件 学生讨论后,板书,回答。 通过几何画板的操作,既巩固了在平移操作中函数k的不变性,也让学生通过操作发现了拦截的不同情况。如此动态的变化,让学生更能感知到数学的魅力。变式2的处理具有一定的难度,通过讨论加强了学生的思想碰撞,也提升了本节课的高度,让学生感受到建模的思想。
活动5 课堂小结通过今天的学习,你有什么体会或收获? 让学生完成本节课知识与方法的小结,再次巩固本节课的内容。师小结:这节课我们利用一次函数等知识解决了实际问题,后续我们还会学习利用一次函数解决其他的问题,以及学习其他函数来解决生活中的问题,正如刚刚同学们所说:数学来源于生活,并应用于生活。 及时总结回顾,帮助学生构建新知识,培养学生的归纳能力和口头表达能力。
活动6 课后思考及作业(1)回顾本节课的所有问题及变式,与同伴探讨尝试提出新的问题并解决。(2)课本P44:练习1,2 教师布置作业,学生课后完成。 巩固并提升所学知识。
板书设计课题学生板书问题(2) 学生板书变式2 s=0.2t+5 Va=0.2 s=0.5t Vb=0.5
六、目标检测设计
课本62页:A组复习题第11题.
如图,甲骑自行车与乙骑摩托车沿相同路线由A地到B地行驶,两地之间的距离是60 km,请根据图象回答:
(1)乙骑摩托车的速度是多少?
(2)甲骑自行车的速度是多少
(3)两人相遇的时候,距B地还有多远?
(4)乙比甲晚多少时间出发,又早到多少时间?
设计意图:让学生体会一次函数在生活中的广泛应用,学习利用一次函数的知识解决问题.
沪科版八年级上册《第12章 一次函数》
教学目标
(1)掌握并运用一次函数的图象和性质,体会数形结合思想和建立函数模型研究数学问题的基本方法.
(2)通过对实际问题图象的分析,进一步加深对一次函数性质的理解.
(3)能够从实际问题中抽象出一次函数关系,并运用一次函数及其性质解决实际问题,发展学生的应用意识.
教学重难点 :理解实际问题中一次函数的模型,并利用所学知识解决问题.
教学过程设计
教学过程设计
问题与情境 师生活动 设计意图
活动1 复习回顾 师:在前面的学习中,我们已经了解了一次函数的定义和性质,我们知道,一次函数的一般形式是。。。(生答)对于一次函数y=0.2x+5,大家能说出k和b在图中的意义吗?学生回答。师:加入了一次函数y=0.5x之后,两个图象的交点坐标大家会求吗?请动手试一试。学生求解出交点坐标。师追问:交点坐标的意义是什么?什么时候y1>y2,什么时候y1
活动3 分析图象,解决问题下图两条直线分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。(1)从图中你能得到哪些信息?(2)15分钟内,B能否追上A (3)当A逃到距离海岸12海里以外的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截 师:下图两条直线分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。从图中你能得到哪些信息?学生通过观察图形,从特殊点、图象的倾斜程度、函数关系式等方面分析并回答。师:同学们从图中得到了很多信息,接下来我们就来看看是否能用这些信息解决下面两个问题:15分钟内,B能否追上A 学生上台板书计算判断的过程。师:当A逃到距离海岸12海里以外的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截 学生回答。(可利用上一问的结果进行本小题的解决) 问题(1)的设计是为了后续两个问题做准备,同时进一步提高学生对图象的分析能力。问题(2)是一次函数解决问题最基本方法的体现,学生可以通过诸如函数等多种方法解答。问题(3)是在前两小题的基础上进行解答,体现的问题的层层递进,不断加深对函数思想的理解和函数方法的掌握。
活动4 探索变式,提升能力变式1:若我国执法船发现可疑船只A的时候,A船距离海岸m海里,派出的追赶快艇B和A船的速度不变,要保证B还能在A进入公海前将其拦截,则m的最大值是多少? 变式2:若A将速度提高至Va,B要保证A逃到公海前将其拦截,B也将速度提高至Vb,那么Va和Vb需要满足什么条件 师:刚刚同学们利用所学的一次函数的知识很好的解决了给出的问题,我们知道,实际问题充满了变化,若将l1向上平移,这样的操作从实际意义来看,什么发生了改变,什么没有改变?学生感知后,思考回答。师追问:若我国执法船发现可疑船只A的时候,A船距离海岸m海里,派出的追赶快艇B和A船的速度不变,要保证B还能在A进入公海前将其拦截,则m的最大值是多少?先由一名学生上台操作几何画板,找到m最大值的情况。学生再计算后回答。师操作:拉动交点P的位置。师:这样的操作从实际意义来看,什么发生了改变,什么没有改变?学生回答。师追问:我们知道,在被发现时间固定的情况下,A船想要逃跑,必须加速。但我们的执法B船肯定会圆满完成任务,顺利拦截。若A将速度提高至Va,B要保证A逃到公海前将其拦截,B也将速度提高至Vb,那么Va和Vb需要满足什么条件 学生讨论后,板书,回答。 通过几何画板的操作,既巩固了在平移操作中函数k的不变性,也让学生通过操作发现了拦截的不同情况。如此动态的变化,让学生更能感知到数学的魅力。变式2的处理具有一定的难度,通过讨论加强了学生的思想碰撞,也提升了本节课的高度,让学生感受到建模的思想。
活动5 课堂小结通过今天的学习,你有什么体会或收获? 让学生完成本节课知识与方法的小结,再次巩固本节课的内容。师小结:这节课我们利用一次函数等知识解决了实际问题,后续我们还会学习利用一次函数解决其他的问题,以及学习其他函数来解决生活中的问题,正如刚刚同学们所说:数学来源于生活,并应用于生活。 及时总结回顾,帮助学生构建新知识,培养学生的归纳能力和口头表达能力。
活动6 课后思考及作业(1)回顾本节课的所有问题及变式,与同伴探讨尝试提出新的问题并解决。(2)课本P44:练习1,2 教师布置作业,学生课后完成。 巩固并提升所学知识。
板书设计课题学生板书问题(2) 学生板书变式2 s=0.2t+5 Va=0.2 s=0.5t Vb=0.5
六、目标检测设计
课本62页:A组复习题第11题.
如图,甲骑自行车与乙骑摩托车沿相同路线由A地到B地行驶,两地之间的距离是60 km,请根据图象回答:
(1)乙骑摩托车的速度是多少?
(2)甲骑自行车的速度是多少
(3)两人相遇的时候,距B地还有多远?
(4)乙比甲晚多少时间出发,又早到多少时间?
设计意图:让学生体会一次函数在生活中的广泛应用,学习利用一次函数的知识解决问题.
