1.3算法与案例
图片预览










文档简介
课件62张PPT。§§1.3算法案例1. 回顾算法的三种表示方法:(1)、自然语言(2)、程序框图(3)、程序语言(三种逻辑结构)(五种基本语句)复习引入2. 思考:小学学过的求两个数的最大公约数的方法? 先用两个公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来.例:求下面两个正整数的最大公约数:(1)求25和35的最大公约数
(2)求49和63的最大公约数所以,25和35的最大公约数为5所以,49和63的最大公约数为7例:如何算出8251和6105的最大公约数?新课讲解:一、辗转相除法(欧几里得算法)1、定义:
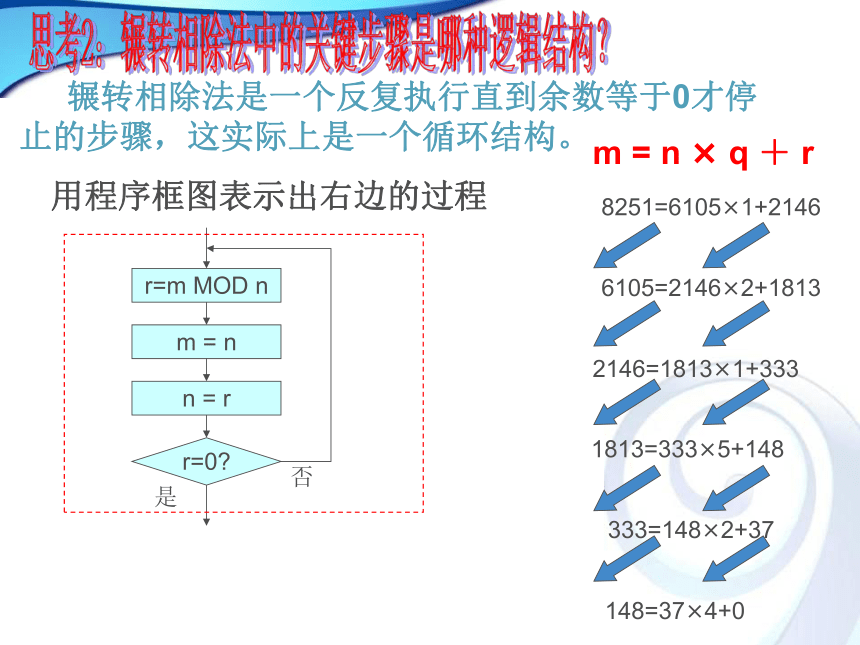
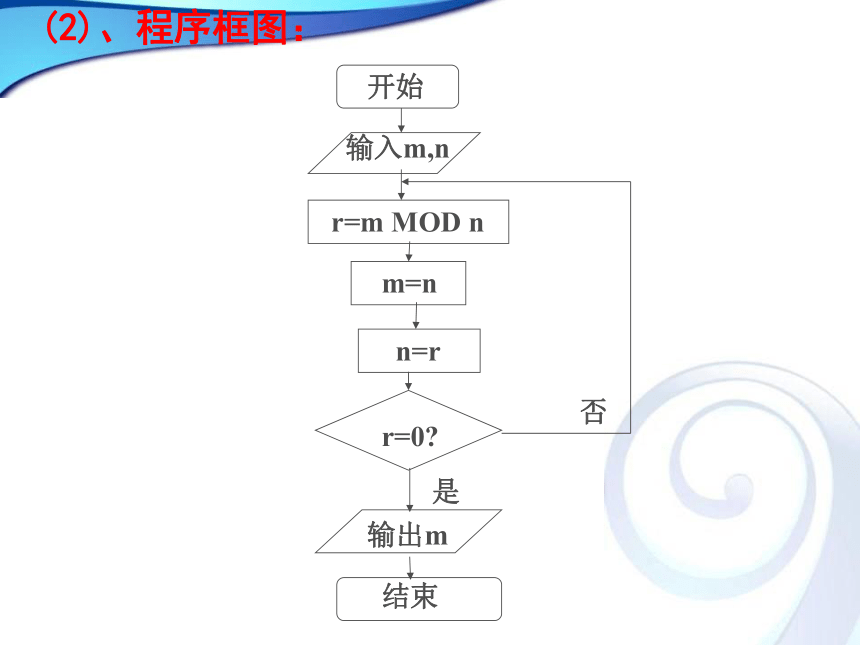
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。 2、步骤:(以求8251和6105的最大公约数的过程为例)第一步 用两数中较大的数除以较小的数,求得商和余数:8251=6105×1+2146结论: 8251和6105的公约数就是6105和2146的公约数,求8251和6105的最大公约数,只要求出6105和2146的最大公约数就可以了。第二步 对6105和2146重复第一步的做法 6105=2146×2+1813 同理6105和2146的最大公约数也是2146和1813的最大公约数。 为什么呢?完整的过程8251=6105×1+2146 6105=2146×2+1813 2146=1813×1+3331813=333×5+148333=148×2+37148=37×4+0显然37是148和37的最大公约数,也就是8251和6105的最大公约数 思考:从上述的过程你体会到了什么?例: 用辗转相除法求225和135的最大公约数225=135×1+90135=90×1+4590=45×2显然45是90和45的最大公约数,也就是225和135的最大公约数 思考1:从上面的两个例子中可以看出计算的规律是什么? S1:用大数除以小数S2:除数变成被除数,余数变成除数S3:重复S1,直到余数为0 辗转相除法是一个反复执行直到余数等于0才停止的步骤,这实际上是一个循环结构。m = n × q + r用程序框图表示出右边的过程r=m MOD nm = nn = rr=0?是否思考2:辗转相除法中的关键步骤是哪种逻辑结构? 思考:你能把辗转相除法编成一个计算机程序吗?(1)、算法步骤:第一步:输入两个正整数m,n(m>n).
第二步:计算m除以n所得的余数r.
第三步:m=n,n=r.
第四步:若r=0,则m,n的最大公约数等于m;
否则,返回第二步.
第五步:输出最大公约数m.(2)、程序框图:(3)、程序:INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END二、更相减损术 可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。第二步:以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的数和差相等为止,则这个等数或这个数与约简的数的乘积就是所求的最大公约数。(1)、《九章算术》中的更相减损术:1、背景介绍:(2)、现代数学中的更相减损术:2、定义: 所谓更相减损术,就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。例: 用更相减损术求98与63的最大公约数.解:由于63不是偶数,把98和63以大数减小数,并辗转相减 98-63=35 63-35=28 35-28=7 28-7=21
21-7=14
14-7=7所以,98和63的最大公约数等于7 3、方法:1、用更相减损术求两个正数84与72的最大公约数. 练习:思路分析:先约简,再求21与18的最大公约数,然后乘以两次约简的质因数4。2、求324、243、135这三个数的最大公约数。思路分析:求三个数的最大公约数可以先求出两个数的最大公约数,第三个数与前两个数的最大公约数的最大公约数即为所求。2、求324、243、135这三个数的最大公约数2、求324、243、135这三个数的最大公约数(1)、算法步骤第一步:输入两个正整数a,b(a>b);
第二步:若a不等于b ,则执行第三步;否则转到第五步;
第三步:把a-b的差赋予r;
第四步:如果b>r, 那么把b赋给a,把r赋给b;否则把r赋给a,执行第二步;
第五步:输出最大公约数b.***思考:你能根据更相减损术设计程序,求两个正整数的最大公约数吗?(2)、程序框图是否是(3)、程序INPUT "a,b=";a,b
WHILE a<>b
r=a-b
IF b>r THEN
a=b
b=r
ELSE
a=r
END IF
WEND
PRINT b
END比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到。小结1、求两个数的最大公约数的两种方法分别是
( )和( )。
2、两个数21672,8127的最大公约数是 ( )
A、2709 B、2606 C、2703 D、2706A辗转相除法更相减损术案例2 秦九韶算法问题怎样求多项式f(x)=x5+x4+x3+x2+x+1
当x=5时的值呢?计算多项式f(x) =x5+x4+x3+x2+x+1当x = 5的值算法1:因为f(x) =x5+x4+x3+x2+x+1所以f(5)=55+54+53+52+5+1=3125+625+125+25+5+1= 3906算法2:f(5)=55+54+53+52+5+1=5×(54+53+52+5+1 ) +1=5×(5×(53+52+5 +1 )+1 ) +1=5×(5×(5×(52+5 +1) +1 ) +1 ) +1=5×(5×(5×(5 ×(5 +1) +1 )+1)+1) +1分析:两种算法中各用了几次乘法运算?和几次加法运算?算法1:算法2:共做了1+2+3+4=10次乘法运算,5次加法运算。共做了4次乘法运算,5次加法运算。《数书九章》——秦九韶算法对该多项式按下面的方式进行改写:思考:当知道了x的值后该如何求多项式的值?这是怎样的一种改写方式?最后的结果是什么?要求多项式的值,应该先算最内层的一次多项式的值,即然后,由内到外逐层计算一次多项式的值,即最后的一项是什么?这种将求一个n次多项式f(x)的值转化成求n个一次多项式的值的方法,称为秦九韶算法。思考:在求多项式的值上,这是怎样的一个转化?算法步骤:第一步:输入多项式次数n、最高次项的系数an和x的值.第二步:将v的值初始化为an,将i的值初始化为n-1.第三步:输入i次项的系数ai第四步:v=vx+ai,i=i-1.第五步:判断i是否小于或等于0,若是,则返回第三步;否则,输出多项式的值v。程序框图:这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现。程序特点:通过一次式的反复计算,逐步得出高次多项式的值,对于一个n次多项式,只需做n次乘法和n次加法即可。例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7v0=2 v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677所以,当x=5时,多项式的值是2677.然后由内向外逐层计算一次多项式的值,即2 -5 -4 3 -6 7x=5105252110510854053426702677所以,当x=5时,多项式的值是2677.原多项式的系数多项式的值.例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法二:列表22 -5 0 -4 3 -6 0x=5105252512512160560830403034所以,当x=5时,多项式的值是15170.练一练:用秦九韶算法求多项式 f(x)=2x6-5x5-4x3+3x2-6x当x=5时的值.解:原多项式先化为:
f(x)=2x6-5x5 +0×x4-4x3+3x2-6x+0
列表21517015170 注意:n次多项式有n+1项,因此缺少哪一项应将其系数补0.例2 已知一个五次多项式为用秦九韶算法求这个多项式当x = 5的值。解:将多项式变形:按由里到外的顺序,依此计算一次多项式当x = 5时的值:所以,当x = 5时,多项式的值等于14130.2你从中看到了怎样的规律?怎么用程序框图来描述呢?程序框图:这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现。练习、已知多项式f(x)=x5+5x4+10x3+10x2+5x+1
用秦九韶算法求这个多项式当x=-2时的值。课堂小结:
1、秦九韶算法的方法和步骤
2、秦九韶算法的程序框图案例三 进位制 [问题1]我们常见的数字都是十进制的,但是并不是生活中的每一种数字都是十进制的.比如时间和角度的单位用六十进位制,电子计算机用的是二进制.那么什么是进位制?不同的进位制之间又有什么联系呢? 进位制是人们为了计数和运算的方便而约定的一种记数系统,约定满二进一,就是二进制;满十进一,就是十进制;满十六进一,就是十六进制;等等. “满几进一”,就是几进制,几进制的基数就是几. 可使用数字符号的个数称为基数.基数都是大于1的整数. 如二进制可使用的数字有0和1,基数是2;
十进制可使用的数字有0,1,2,…,8,9等十个数字,基数是10;
十六进制可使用的数字或符号有0~9等10个数字以及A~F等6个字母(规定字母A~F对应10~15),十六进制的基数是16. 注意:为了区分不同的进位制,常在数字的右下脚标明基数. 如111001(2)表示二进制数,34(5)表示5进制数.十进制数一般不标注基数.[问题2]十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,从而它可以写成下面的形式:3721=3×103+7×102+2×101+1×100. 想一想二进制数1011(2)可以类似的写成什么形式?1011(2)=1×23+0×22+1×21+1×20.同理:3421(5)=3×53+4×52+2×51+1×50.C7A16(16)=12×164+7×163+10×162+1×161+6×160 一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式anan-1…a1a0(k) (0(2)每一个数字an,an-1,…,a1,a0都须小于k. k进制的数也可以表示成不同位上数字与基数k的幂的乘积之和的形式,即anan-1…a1a0(k)=an×kn+an-1×kn-1
+…+a1×k1+a0×k0 .注意这是一个n+1位数. [问题3]二进制只用0和1两个数字,这正好与电路的通和断两种状态相对应,因此计算机内部都使用二进制.计算机在进行数的运算时,先把接受到的数转化成二进制数进行运算,再把运算结果转化为十进制数输出.
那么二进制数与十进制数之间是如何转化的呢?例1:把二进制数110011(2)化为十进制数. 分析:先把二进制数写成不同位上数字与2的幂的乘积之和的形式,再按照十进制数的运算规则计算出结果.解:110011(2)
=1×25+1×24+0×23+0×22+1×21+1×20
=1×32+1×16+1×2+1=51.[问题4]你会把三进制数10221(3)化为十进制数吗?解:10221(3)=1×34+0×33+2×32+2×31+1×30
=81+18+6+1=106. k进制数转化为十进制数的方法 先把k进制的数表示成不同位上数字与基数k的幂的乘积之和的形式,即anan-1…a1a0(k)
=an×kn+an-1×kn-1+…+a1×k1+a0×k0 .再按照十进制数的运算规则计算出结果.例2.设计一个算法,把k进制数a(共有n位)化为十进制数b.开始输入a,k,nb=0i=1①①把a的右数第i位数字赋给tb=b+t*ki-1i=i+1i>n?否是输出b结束程序框图:INPUT a,k,ni=1b=0DOb=b+t*k^(i-1)i=i+1LOOP UNTIL i>nPRINT bENDt=a MOD 10a=a10t=a MOD 10程序:例3:把89化为二进制的数. 分析:把89化为二进制的数,需想办法将89先写成如下形式89=an×2n+an-1×2n-1+…+a1×21+a0×20 .89=64+16+8+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20
=1011001(2).但如果数太大,我们是无法这样凑出来的,怎么办?89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1, 89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 89=44×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
=(((5×2+1)×2+0)×2+0)×2+1
=((((2×2+1)×2+1)×2+0)× 2+0)×2+1
=(((((1×2)+0)×2+1)×2+1)×2+0)× 2+0)×2+1=1×26+0×25+1×24+1×23+0×22+0×21+1×20=1011001(2).可以用2连续去除89或所得商(一直到商为0为止),然后取余数
---除2取余法.2=1×2+0, 1=0×2+1, 44 1例3:把89化为二进制的数.我们可以用下面的除法算式表示除2取余法:22 011 05 12 11 00 1把算式中各步所得的余数从下到上排列,得到89=1011001(2).这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.例4:把89化为五进制的数.解:以5作为除数,相应的除法算式为:17 43 20 3∴ 89=324(5).开始输入a,k求a除以k的商q求a除以k的余数r①把得到的余数依次从右到左排列否结束输出全部余数r排列得到的k进制数a=qq=0?是①INPUT “a,k=” ;a,k
b=0
i=0
DO
q=ak
r=a MOD k
b=b+r*10^i
i=i+1
a=q
LOOP UNTIL q=0
PRINT b
END[问题5]你会把三进制数10221(3)化为二进制数吗?解:第一步:先把三进制数化为十进制数:
10221(3)=1×34+0×33+2×32+2×31+1×30
=81+18+6+1=106. 第二步:再把十进制数化为二进制数: 106=1101010(2).小结进位制的概念及表示方法;
各种进位制之间的相互转化.anan-1…a1a0(k)
=an×kn+an-1×kn-1+…+a1×k1+a0×k0 .作业:
1.课本P45页A组T3.
下课了!
(2)求49和63的最大公约数所以,25和35的最大公约数为5所以,49和63的最大公约数为7例:如何算出8251和6105的最大公约数?新课讲解:一、辗转相除法(欧几里得算法)1、定义:
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。 2、步骤:(以求8251和6105的最大公约数的过程为例)第一步 用两数中较大的数除以较小的数,求得商和余数:8251=6105×1+2146结论: 8251和6105的公约数就是6105和2146的公约数,求8251和6105的最大公约数,只要求出6105和2146的最大公约数就可以了。第二步 对6105和2146重复第一步的做法 6105=2146×2+1813 同理6105和2146的最大公约数也是2146和1813的最大公约数。 为什么呢?完整的过程8251=6105×1+2146 6105=2146×2+1813 2146=1813×1+3331813=333×5+148333=148×2+37148=37×4+0显然37是148和37的最大公约数,也就是8251和6105的最大公约数 思考:从上述的过程你体会到了什么?例: 用辗转相除法求225和135的最大公约数225=135×1+90135=90×1+4590=45×2显然45是90和45的最大公约数,也就是225和135的最大公约数 思考1:从上面的两个例子中可以看出计算的规律是什么? S1:用大数除以小数S2:除数变成被除数,余数变成除数S3:重复S1,直到余数为0 辗转相除法是一个反复执行直到余数等于0才停止的步骤,这实际上是一个循环结构。m = n × q + r用程序框图表示出右边的过程r=m MOD nm = nn = rr=0?是否思考2:辗转相除法中的关键步骤是哪种逻辑结构? 思考:你能把辗转相除法编成一个计算机程序吗?(1)、算法步骤:第一步:输入两个正整数m,n(m>n).
第二步:计算m除以n所得的余数r.
第三步:m=n,n=r.
第四步:若r=0,则m,n的最大公约数等于m;
否则,返回第二步.
第五步:输出最大公约数m.(2)、程序框图:(3)、程序:INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END二、更相减损术 可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。第二步:以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的数和差相等为止,则这个等数或这个数与约简的数的乘积就是所求的最大公约数。(1)、《九章算术》中的更相减损术:1、背景介绍:(2)、现代数学中的更相减损术:2、定义: 所谓更相减损术,就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。例: 用更相减损术求98与63的最大公约数.解:由于63不是偶数,把98和63以大数减小数,并辗转相减 98-63=35 63-35=28 35-28=7 28-7=21
21-7=14
14-7=7所以,98和63的最大公约数等于7 3、方法:1、用更相减损术求两个正数84与72的最大公约数. 练习:思路分析:先约简,再求21与18的最大公约数,然后乘以两次约简的质因数4。2、求324、243、135这三个数的最大公约数。思路分析:求三个数的最大公约数可以先求出两个数的最大公约数,第三个数与前两个数的最大公约数的最大公约数即为所求。2、求324、243、135这三个数的最大公约数2、求324、243、135这三个数的最大公约数(1)、算法步骤第一步:输入两个正整数a,b(a>b);
第二步:若a不等于b ,则执行第三步;否则转到第五步;
第三步:把a-b的差赋予r;
第四步:如果b>r, 那么把b赋给a,把r赋给b;否则把r赋给a,执行第二步;
第五步:输出最大公约数b.***思考:你能根据更相减损术设计程序,求两个正整数的最大公约数吗?(2)、程序框图是否是(3)、程序INPUT "a,b=";a,b
WHILE a<>b
r=a-b
IF b>r THEN
a=b
b=r
ELSE
a=r
END IF
WEND
PRINT b
END比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到。小结1、求两个数的最大公约数的两种方法分别是
( )和( )。
2、两个数21672,8127的最大公约数是 ( )
A、2709 B、2606 C、2703 D、2706A辗转相除法更相减损术案例2 秦九韶算法问题怎样求多项式f(x)=x5+x4+x3+x2+x+1
当x=5时的值呢?计算多项式f(x) =x5+x4+x3+x2+x+1当x = 5的值算法1:因为f(x) =x5+x4+x3+x2+x+1所以f(5)=55+54+53+52+5+1=3125+625+125+25+5+1= 3906算法2:f(5)=55+54+53+52+5+1=5×(54+53+52+5+1 ) +1=5×(5×(53+52+5 +1 )+1 ) +1=5×(5×(5×(52+5 +1) +1 ) +1 ) +1=5×(5×(5×(5 ×(5 +1) +1 )+1)+1) +1分析:两种算法中各用了几次乘法运算?和几次加法运算?算法1:算法2:共做了1+2+3+4=10次乘法运算,5次加法运算。共做了4次乘法运算,5次加法运算。《数书九章》——秦九韶算法对该多项式按下面的方式进行改写:思考:当知道了x的值后该如何求多项式的值?这是怎样的一种改写方式?最后的结果是什么?要求多项式的值,应该先算最内层的一次多项式的值,即然后,由内到外逐层计算一次多项式的值,即最后的一项是什么?这种将求一个n次多项式f(x)的值转化成求n个一次多项式的值的方法,称为秦九韶算法。思考:在求多项式的值上,这是怎样的一个转化?算法步骤:第一步:输入多项式次数n、最高次项的系数an和x的值.第二步:将v的值初始化为an,将i的值初始化为n-1.第三步:输入i次项的系数ai第四步:v=vx+ai,i=i-1.第五步:判断i是否小于或等于0,若是,则返回第三步;否则,输出多项式的值v。程序框图:这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现。程序特点:通过一次式的反复计算,逐步得出高次多项式的值,对于一个n次多项式,只需做n次乘法和n次加法即可。例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7v0=2 v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677所以,当x=5时,多项式的值是2677.然后由内向外逐层计算一次多项式的值,即2 -5 -4 3 -6 7x=5105252110510854053426702677所以,当x=5时,多项式的值是2677.原多项式的系数多项式的值.例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法二:列表22 -5 0 -4 3 -6 0x=5105252512512160560830403034所以,当x=5时,多项式的值是15170.练一练:用秦九韶算法求多项式 f(x)=2x6-5x5-4x3+3x2-6x当x=5时的值.解:原多项式先化为:
f(x)=2x6-5x5 +0×x4-4x3+3x2-6x+0
列表21517015170 注意:n次多项式有n+1项,因此缺少哪一项应将其系数补0.例2 已知一个五次多项式为用秦九韶算法求这个多项式当x = 5的值。解:将多项式变形:按由里到外的顺序,依此计算一次多项式当x = 5时的值:所以,当x = 5时,多项式的值等于14130.2你从中看到了怎样的规律?怎么用程序框图来描述呢?程序框图:这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现。练习、已知多项式f(x)=x5+5x4+10x3+10x2+5x+1
用秦九韶算法求这个多项式当x=-2时的值。课堂小结:
1、秦九韶算法的方法和步骤
2、秦九韶算法的程序框图案例三 进位制 [问题1]我们常见的数字都是十进制的,但是并不是生活中的每一种数字都是十进制的.比如时间和角度的单位用六十进位制,电子计算机用的是二进制.那么什么是进位制?不同的进位制之间又有什么联系呢? 进位制是人们为了计数和运算的方便而约定的一种记数系统,约定满二进一,就是二进制;满十进一,就是十进制;满十六进一,就是十六进制;等等. “满几进一”,就是几进制,几进制的基数就是几. 可使用数字符号的个数称为基数.基数都是大于1的整数. 如二进制可使用的数字有0和1,基数是2;
十进制可使用的数字有0,1,2,…,8,9等十个数字,基数是10;
十六进制可使用的数字或符号有0~9等10个数字以及A~F等6个字母(规定字母A~F对应10~15),十六进制的基数是16. 注意:为了区分不同的进位制,常在数字的右下脚标明基数. 如111001(2)表示二进制数,34(5)表示5进制数.十进制数一般不标注基数.[问题2]十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,从而它可以写成下面的形式:3721=3×103+7×102+2×101+1×100. 想一想二进制数1011(2)可以类似的写成什么形式?1011(2)=1×23+0×22+1×21+1×20.同理:3421(5)=3×53+4×52+2×51+1×50.C7A16(16)=12×164+7×163+10×162+1×161+6×160 一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式anan-1…a1a0(k) (0
+…+a1×k1+a0×k0 .注意这是一个n+1位数. [问题3]二进制只用0和1两个数字,这正好与电路的通和断两种状态相对应,因此计算机内部都使用二进制.计算机在进行数的运算时,先把接受到的数转化成二进制数进行运算,再把运算结果转化为十进制数输出.
那么二进制数与十进制数之间是如何转化的呢?例1:把二进制数110011(2)化为十进制数. 分析:先把二进制数写成不同位上数字与2的幂的乘积之和的形式,再按照十进制数的运算规则计算出结果.解:110011(2)
=1×25+1×24+0×23+0×22+1×21+1×20
=1×32+1×16+1×2+1=51.[问题4]你会把三进制数10221(3)化为十进制数吗?解:10221(3)=1×34+0×33+2×32+2×31+1×30
=81+18+6+1=106. k进制数转化为十进制数的方法 先把k进制的数表示成不同位上数字与基数k的幂的乘积之和的形式,即anan-1…a1a0(k)
=an×kn+an-1×kn-1+…+a1×k1+a0×k0 .再按照十进制数的运算规则计算出结果.例2.设计一个算法,把k进制数a(共有n位)化为十进制数b.开始输入a,k,nb=0i=1①①把a的右数第i位数字赋给tb=b+t*ki-1i=i+1i>n?否是输出b结束程序框图:INPUT a,k,ni=1b=0DOb=b+t*k^(i-1)i=i+1LOOP UNTIL i>nPRINT bENDt=a MOD 10a=a10t=a MOD 10程序:例3:把89化为二进制的数. 分析:把89化为二进制的数,需想办法将89先写成如下形式89=an×2n+an-1×2n-1+…+a1×21+a0×20 .89=64+16+8+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20
=1011001(2).但如果数太大,我们是无法这样凑出来的,怎么办?89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1, 89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 89=44×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
=(((5×2+1)×2+0)×2+0)×2+1
=((((2×2+1)×2+1)×2+0)× 2+0)×2+1
=(((((1×2)+0)×2+1)×2+1)×2+0)× 2+0)×2+1=1×26+0×25+1×24+1×23+0×22+0×21+1×20=1011001(2).可以用2连续去除89或所得商(一直到商为0为止),然后取余数
---除2取余法.2=1×2+0, 1=0×2+1, 44 1例3:把89化为二进制的数.我们可以用下面的除法算式表示除2取余法:22 011 05 12 11 00 1把算式中各步所得的余数从下到上排列,得到89=1011001(2).这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.例4:把89化为五进制的数.解:以5作为除数,相应的除法算式为:17 43 20 3∴ 89=324(5).开始输入a,k求a除以k的商q求a除以k的余数r①把得到的余数依次从右到左排列否结束输出全部余数r排列得到的k进制数a=qq=0?是①INPUT “a,k=” ;a,k
b=0
i=0
DO
q=ak
r=a MOD k
b=b+r*10^i
i=i+1
a=q
LOOP UNTIL q=0
PRINT b
END[问题5]你会把三进制数10221(3)化为二进制数吗?解:第一步:先把三进制数化为十进制数:
10221(3)=1×34+0×33+2×32+2×31+1×30
=81+18+6+1=106. 第二步:再把十进制数化为二进制数: 106=1101010(2).小结进位制的概念及表示方法;
各种进位制之间的相互转化.anan-1…a1a0(k)
=an×kn+an-1×kn-1+…+a1×k1+a0×k0 .作业:
1.课本P45页A组T3.
下课了!
