函数的图像和性质
图片预览






文档简介
课件15张PPT。函数的性质及应用知识回顾:已知函数f(x)=x2+2ax+2 x∈[-5,5]
(1) 当a=-1时,求函数f(x)的最大值和最小值.
(2) 求实数a的取值范围,使y= f(x)在区间 [-5,5]上是单调函数.
回顾拓展】含有参变数字母的二次函数的最值问题,主要体现在顶点的变化和区间的变化,当然还有抛物线的开口方向问题,当抛物线开口方向确定时,可能会出现三种情形:
(1)顶点(对称轴)不动,而区间变化(移动);
(2)顶点(对称轴)可移动,而区间不动;
(3)顶点(对称轴)和区间都可移动.无论哪种情形都结合图象、顶点(对称轴)与区间的位置关系对种种可能的情形进行讨论.
旧知操练:函数f(x)=x2-4x-4在闭区间[t,t+1] (t∈R)上的最小值
记为g(t).
(1)试写出g(t)的函数表达式;
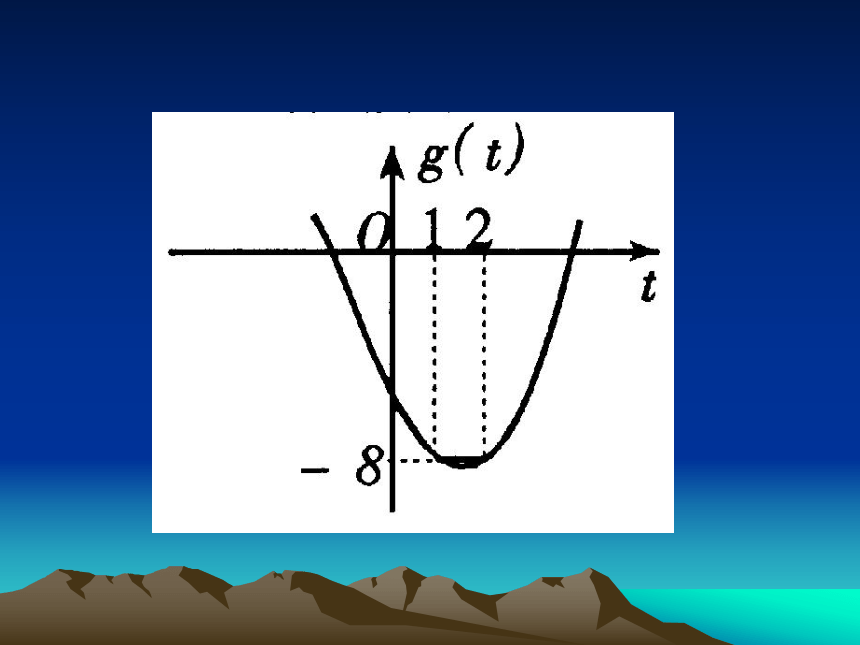
(2)作g(t)的图象并写出g(t)的最小值
【解题回顾】含有参数的二次函数的最值问题,因其顶点相对于定义域区间的位置不同,其最值状况也不同.所以要根据二者的相关位置进行分类讨论本题是“定”二次函数,“动”区间,依照此法也可以讨论“动”二次函数,“定”区间的二次函数问题
2. 求f(x)=x2-2ax+2在[2,4]上的最大值和最小值.问题探究:已知函数f(x)=x2-2ax-1 x∈[-1,3], 问:
1). 是否存在a∈R,使f(x)max=-1
2). 设 g(x) = f(x)max a∈R, 求 g(x)∈———
3)设 h(a)= f(x)min a∈R,
求h(a)∈--------------------展望高考:1(08陕西) 设函数 f(x)=x3+ax2-a2x+1, g(x)=ax2-2x +1,其中a ≠0
① 若a﹥0,求f(x)的单调区间。
② 当函数y=f(x)与y=g(x)的图象只有 一个公共点,且g(x)存在最小值时,记g(x)的最小值为h(a )
求 : h(a)的 值域。
③ 若f(x)与g(x)在区间(a,a+2)内均为增函数,求a的取值范围。
2 已知函数f(x)=x3+bx2+cx 的导函数的图象关于直线x=2 对 称,
① 求b的值
② 若f(x)在x=t处取得极小
值,记此极小值为g(t),
求: g(t)的定义域和值域
(1) 当a=-1时,求函数f(x)的最大值和最小值.
(2) 求实数a的取值范围,使y= f(x)在区间 [-5,5]上是单调函数.
回顾拓展】含有参变数字母的二次函数的最值问题,主要体现在顶点的变化和区间的变化,当然还有抛物线的开口方向问题,当抛物线开口方向确定时,可能会出现三种情形:
(1)顶点(对称轴)不动,而区间变化(移动);
(2)顶点(对称轴)可移动,而区间不动;
(3)顶点(对称轴)和区间都可移动.无论哪种情形都结合图象、顶点(对称轴)与区间的位置关系对种种可能的情形进行讨论.
旧知操练:函数f(x)=x2-4x-4在闭区间[t,t+1] (t∈R)上的最小值
记为g(t).
(1)试写出g(t)的函数表达式;
(2)作g(t)的图象并写出g(t)的最小值
【解题回顾】含有参数的二次函数的最值问题,因其顶点相对于定义域区间的位置不同,其最值状况也不同.所以要根据二者的相关位置进行分类讨论本题是“定”二次函数,“动”区间,依照此法也可以讨论“动”二次函数,“定”区间的二次函数问题
2. 求f(x)=x2-2ax+2在[2,4]上的最大值和最小值.问题探究:已知函数f(x)=x2-2ax-1 x∈[-1,3], 问:
1). 是否存在a∈R,使f(x)max=-1
2). 设 g(x) = f(x)max a∈R, 求 g(x)∈———
3)设 h(a)= f(x)min a∈R,
求h(a)∈--------------------展望高考:1(08陕西) 设函数 f(x)=x3+ax2-a2x+1, g(x)=ax2-2x +1,其中a ≠0
① 若a﹥0,求f(x)的单调区间。
② 当函数y=f(x)与y=g(x)的图象只有 一个公共点,且g(x)存在最小值时,记g(x)的最小值为h(a )
求 : h(a)的 值域。
③ 若f(x)与g(x)在区间(a,a+2)内均为增函数,求a的取值范围。
2 已知函数f(x)=x3+bx2+cx 的导函数的图象关于直线x=2 对 称,
① 求b的值
② 若f(x)在x=t处取得极小
值,记此极小值为g(t),
求: g(t)的定义域和值域
