第10章 相交线、平行线 复习(2) 课件(共29张PPT)
文档属性
| 名称 | 第10章 相交线、平行线 复习(2) 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 957.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 16:54:26 | ||
图片预览





文档简介
(共29张PPT)
沪科版 七年级下册
第10章 相交线、平行线 复习(2)
平行线判定与性质
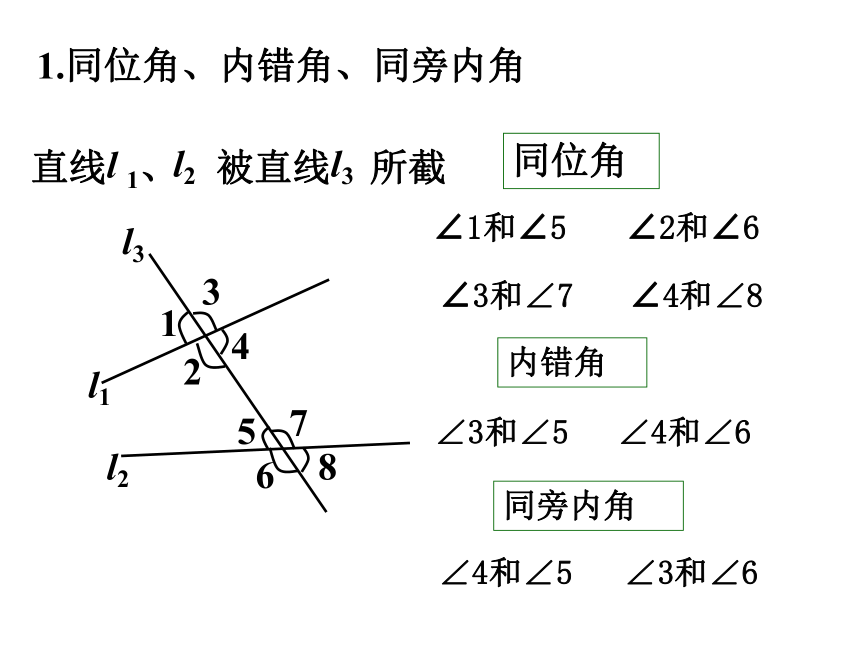
同位角
内错角
同旁内角
∠1和∠5
∠4和∠8
∠2和∠6
∠3和∠7
∠3和∠5
∠4和∠6
∠4和∠5
∠3和∠6
1.同位角、内错角、同旁内角
直线 1、 被直线 所截
l
l2
l3
1
5
7
6
8
l1
l2
l3
3
2
4
(1)平行线的定义:
经过已知直线外一点,有且只有一条直线与已知直线平行.
在同一平面内,不相交的两条直线,叫做平行线.
(2)平行公理
2.平行线
①在同一平面内不相交的两条直线平行;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④同旁内角互补,两直线平行.
⑤同一平面内垂直于同一条直线的两直线平行.
⑥平行于同一条直线的两条直线平行.
(3)平行线的判定
①两条直线平行,同位角相等;
②两条直线平行,内错角相等;
③两条直线平行,同旁内角互补.
(4)平行线的性质
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(1)平移的定义
3.平移
①平移前后,图形的形状和大小完全相同.
(2)平移的性质:
②经过平移,对应点所连的线段平行(或在同一条直线上)且相等.
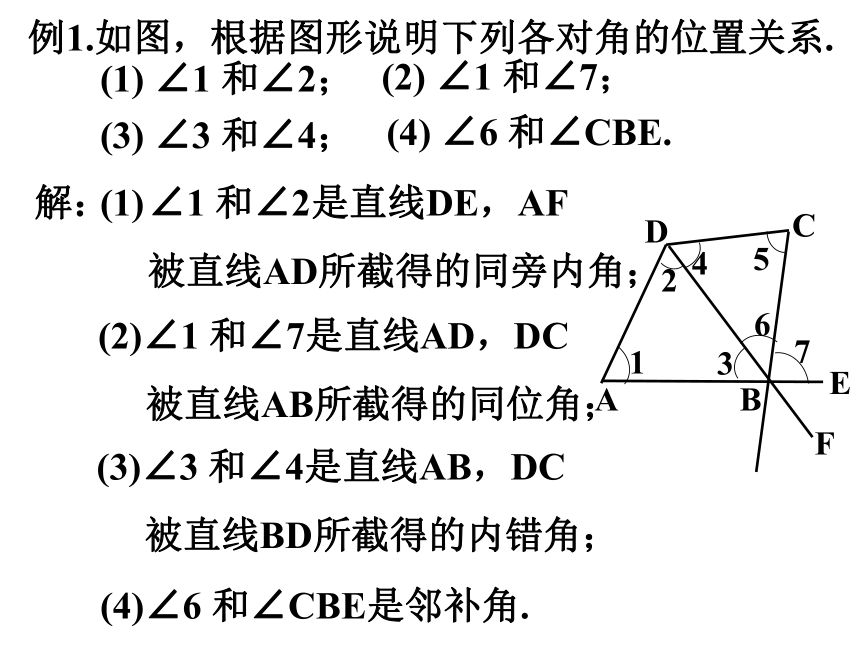
例1.如图,根据图形说明下列各对角的位置关系.
(1) ∠1 和∠2;
(2) ∠1 和∠7;
(3) ∠3 和∠4;
(4) ∠6 和∠CBE.
B
A
C
D
F
E
1
2
4
3
5
6
7
∠1 和∠2是直线DE,AF
被直线AD所截得的同旁内角;
(2)∠1 和∠7是直线AD,DC
被直线AB所截得的同位角;
(3)∠3 和∠4是直线AB,DC
被直线BD所截得的内错角;
(4)∠6 和∠CBE是邻补角.
解:
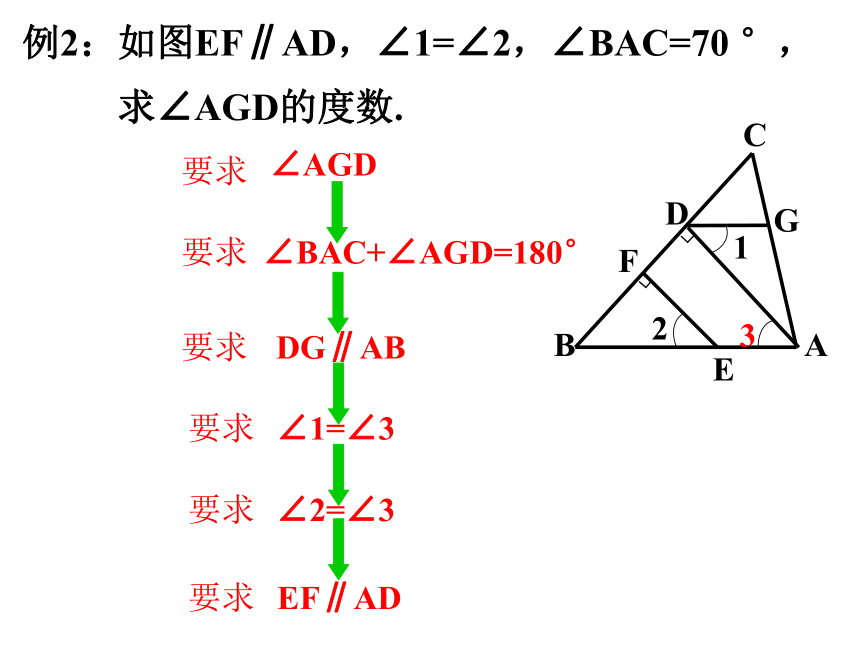
例2:如图EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.
EF∥AD
∠2=∠3
∠1=∠3
DG∥AB
∠BAC+∠AGD=180°
∠AGD
要求
要求
要求
要求
要求
要求
D
F
C
B
A
∟
∟
G
E
1
2
3
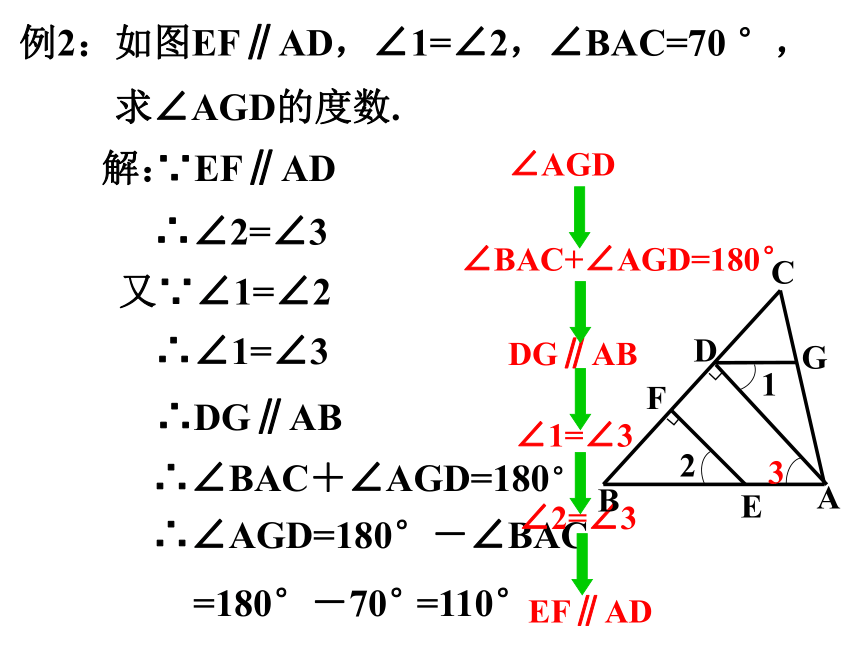
例2:如图EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.
解:
∵EF∥AD
∴∠2=∠3
又∵∠1=∠2
∴∠1=∠3
∴DG∥AB
∴∠BAC+∠AGD=180°
∴∠AGD=180°-∠BAC
EF∥AD
∠2=∠3
∠1=∠3
DG∥AB
∠BAC+∠AGD=180°
∠AGD
D
F
C
B
A
∟
∟
G
E
1
2
3
=180°-70°
=110°
例3.如图,AD∥BC,且AD<BC,将△ABC平移到△DEF的位置.
A
C
B
D
F
E
(1) 指出平移的方向和平移的距离;
(2) 试说明AD+BC=BF.
解:
指出平移的方向是
点A到点D的方向;
平移的距离是线段AD的长度;
(2) 根据平移的性质,得
CF=AD
∴AD+BC=BF.
∵ CF+BC=BF,
1.如图1,下列说法错误的是( ).
A.∠1与∠4是内错角 B. ∠2与∠A是同位角
C. ∠3与∠C是同旁内角 D. ∠B与∠C是同旁内角
练习巩固
一.选择题
图1
A
B
C
C
2.如图,若∠1=∠2,可以得出那个结果( )
A.AB//CD B.AB=CD
C.AD//BC D.∠B=∠D
A
C
B
A
D
3.如图,下列条件能判定l1// l2的是( )
1
5
l1
l2
l3
3
2
4
l4
A.∠1=∠2 B.∠1=∠5
C.∠1+∠3=180° D.∠3=∠5
C
4.如图,下列不能判定AB//CD的条件是( )
A.∠1=∠2 B.∠B+∠BCD=180°
C.∠3=∠4 D. ∠B=∠5
1
5
C
B
A
3
2
4
D
E
A
5.如图,AB//CD,BC平分∠ABD.若∠C=40°,
则∠D的度数是( ).
A.90° B.100° C.110° D. 120°
C
B
A
D
C
6.如图,已知∠1=70°,若BE//CD,那么∠B
的度数是( ).
A.70° B.100° C.110° D. 120°
C
B
A
D
E
1
C
7.如图,AB//CD,点E,F分别在直线AB,CD
上,∠EPF=90°,∠BEP=∠GEP,则∠1与
∠2的数量关系是( ).
A.∠1=∠2 B.∠1=2∠2
C.∠1=3∠2 D. ∠1=4∠2
C
B
A
D
E
G
P
F
1
2
B
8.如图,将△ABC向右平移后得到△DEF,则∠C的对应角和ED的对应边分别是( ).
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
A
B
C
D
E
F
O
C
9.如图,直线a//b,直线l与a相交于点P,
与直线b相交于点Q,且PM于l于点P.
若∠1=58°,则∠2= .
二.填空题
1
a
b
M
2
l
P
32°
10.如图,已知AB//CD,CE平分∠ACD.
当∠A=100°,∠ECD的度数是 .
A
C
D
B
E
40°
11.如图,将△ABC向右平移后得到△DEF,则平移的距离是线段 的长度;若∠ACB=75°,则∠F= °.
A
C
B
D
F
E
EC
75
12.如图,将△ABC向平移到△DEF,可以先将ABC向右平移 格 ;再向上平移 格.
C
A
B
F
D
E
6
3
13.如图,EF∥AD, ∠1=∠2,∠BAC=70°,
将求∠AGD的过程填写完整.
解:∵EF∥AD,(已知)
∴∠2= ∠3.( )
又∵∠1=∠2,(已知)
∴∠1= .( 等量代换)
∴AB∥ .( )
∴∠BAC+∠DGA =180°( )
又∵∠BAC=70°,(已知)
∴∠AGD= .
D
F
C
B
A
∟
∟
G
E
1
2
3
两直线平行,同位角相等.
∠3
DG
内错角相等,两直线平行
110°
两直线平行,同旁内角互补
A
B
C
∟
∟
D
G
E
1
2
3
14.如图,已知AD⊥BC,EG⊥BC,垂足分别为D,G,又∠GEC=∠3, 那么AD平分∠BAC吗?为什么?
解:
AD平分∠BAC.
∵ AD⊥BC,EG⊥BC,
∴ AD∥EG.
∴∠2=∠3,
∵∠GEC=∠3,
∠1=∠GEC,
∴∠1=∠2.
∴AD平分∠BAC.
三.解答题
15.如图,已知∠1=∠BDC, ∠2+∠3=180°.
(1) AD∥EC吗?请说明理由.
(2) 已知DA平分∠BDC , CE⊥AE于点E,
∠1=70°,求∠FAB的度数.
解:
AD∥EC.
(1)
理由如下:
∵∠1=∠BDC,
∴ AB∥CD.
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴ ∠ADC+∠3=180°.
∴ AD∥EC.
D
1
A
B
C
∟
F
2
3
E
15.如图,已知∠1=∠BDC, ∠2+∠3=180°.
(2) 已知DA平分∠BDC , CE⊥AE于点E,
∠1=70°,求∠FAB的度数.
D
1
A
B
C
∟
F
2
3
E
(2)
∠1=70°,
=55°.
∴∠ADC= ∠BDC
=90°-35°
∴ ∠FAD=∠AEC=90°.
∵ AD∥EC,
∵DA平分∠BDC ,
∴∠FAB=∠FAD-∠2
∵CE⊥AE,
∴∠AEC=90°.
1
2
= ∠1= ×70°
=35°,
1
2
1
2
16.如图,将方格中的“机器人”图形向右平移3格 ;再向下平移3格,在方格中画出平移后得到的图形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级下册
第10章 相交线、平行线 复习(2)
平行线判定与性质
同位角
内错角
同旁内角
∠1和∠5
∠4和∠8
∠2和∠6
∠3和∠7
∠3和∠5
∠4和∠6
∠4和∠5
∠3和∠6
1.同位角、内错角、同旁内角
直线 1、 被直线 所截
l
l2
l3
1
5
7
6
8
l1
l2
l3
3
2
4
(1)平行线的定义:
经过已知直线外一点,有且只有一条直线与已知直线平行.
在同一平面内,不相交的两条直线,叫做平行线.
(2)平行公理
2.平行线
①在同一平面内不相交的两条直线平行;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④同旁内角互补,两直线平行.
⑤同一平面内垂直于同一条直线的两直线平行.
⑥平行于同一条直线的两条直线平行.
(3)平行线的判定
①两条直线平行,同位角相等;
②两条直线平行,内错角相等;
③两条直线平行,同旁内角互补.
(4)平行线的性质
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(1)平移的定义
3.平移
①平移前后,图形的形状和大小完全相同.
(2)平移的性质:
②经过平移,对应点所连的线段平行(或在同一条直线上)且相等.
例1.如图,根据图形说明下列各对角的位置关系.
(1) ∠1 和∠2;
(2) ∠1 和∠7;
(3) ∠3 和∠4;
(4) ∠6 和∠CBE.
B
A
C
D
F
E
1
2
4
3
5
6
7
∠1 和∠2是直线DE,AF
被直线AD所截得的同旁内角;
(2)∠1 和∠7是直线AD,DC
被直线AB所截得的同位角;
(3)∠3 和∠4是直线AB,DC
被直线BD所截得的内错角;
(4)∠6 和∠CBE是邻补角.
解:
例2:如图EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.
EF∥AD
∠2=∠3
∠1=∠3
DG∥AB
∠BAC+∠AGD=180°
∠AGD
要求
要求
要求
要求
要求
要求
D
F
C
B
A
∟
∟
G
E
1
2
3
例2:如图EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.
解:
∵EF∥AD
∴∠2=∠3
又∵∠1=∠2
∴∠1=∠3
∴DG∥AB
∴∠BAC+∠AGD=180°
∴∠AGD=180°-∠BAC
EF∥AD
∠2=∠3
∠1=∠3
DG∥AB
∠BAC+∠AGD=180°
∠AGD
D
F
C
B
A
∟
∟
G
E
1
2
3
=180°-70°
=110°
例3.如图,AD∥BC,且AD<BC,将△ABC平移到△DEF的位置.
A
C
B
D
F
E
(1) 指出平移的方向和平移的距离;
(2) 试说明AD+BC=BF.
解:
指出平移的方向是
点A到点D的方向;
平移的距离是线段AD的长度;
(2) 根据平移的性质,得
CF=AD
∴AD+BC=BF.
∵ CF+BC=BF,
1.如图1,下列说法错误的是( ).
A.∠1与∠4是内错角 B. ∠2与∠A是同位角
C. ∠3与∠C是同旁内角 D. ∠B与∠C是同旁内角
练习巩固
一.选择题
图1
A
B
C
C
2.如图,若∠1=∠2,可以得出那个结果( )
A.AB//CD B.AB=CD
C.AD//BC D.∠B=∠D
A
C
B
A
D
3.如图,下列条件能判定l1// l2的是( )
1
5
l1
l2
l3
3
2
4
l4
A.∠1=∠2 B.∠1=∠5
C.∠1+∠3=180° D.∠3=∠5
C
4.如图,下列不能判定AB//CD的条件是( )
A.∠1=∠2 B.∠B+∠BCD=180°
C.∠3=∠4 D. ∠B=∠5
1
5
C
B
A
3
2
4
D
E
A
5.如图,AB//CD,BC平分∠ABD.若∠C=40°,
则∠D的度数是( ).
A.90° B.100° C.110° D. 120°
C
B
A
D
C
6.如图,已知∠1=70°,若BE//CD,那么∠B
的度数是( ).
A.70° B.100° C.110° D. 120°
C
B
A
D
E
1
C
7.如图,AB//CD,点E,F分别在直线AB,CD
上,∠EPF=90°,∠BEP=∠GEP,则∠1与
∠2的数量关系是( ).
A.∠1=∠2 B.∠1=2∠2
C.∠1=3∠2 D. ∠1=4∠2
C
B
A
D
E
G
P
F
1
2
B
8.如图,将△ABC向右平移后得到△DEF,则∠C的对应角和ED的对应边分别是( ).
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
A
B
C
D
E
F
O
C
9.如图,直线a//b,直线l与a相交于点P,
与直线b相交于点Q,且PM于l于点P.
若∠1=58°,则∠2= .
二.填空题
1
a
b
M
2
l
P
32°
10.如图,已知AB//CD,CE平分∠ACD.
当∠A=100°,∠ECD的度数是 .
A
C
D
B
E
40°
11.如图,将△ABC向右平移后得到△DEF,则平移的距离是线段 的长度;若∠ACB=75°,则∠F= °.
A
C
B
D
F
E
EC
75
12.如图,将△ABC向平移到△DEF,可以先将ABC向右平移 格 ;再向上平移 格.
C
A
B
F
D
E
6
3
13.如图,EF∥AD, ∠1=∠2,∠BAC=70°,
将求∠AGD的过程填写完整.
解:∵EF∥AD,(已知)
∴∠2= ∠3.( )
又∵∠1=∠2,(已知)
∴∠1= .( 等量代换)
∴AB∥ .( )
∴∠BAC+∠DGA =180°( )
又∵∠BAC=70°,(已知)
∴∠AGD= .
D
F
C
B
A
∟
∟
G
E
1
2
3
两直线平行,同位角相等.
∠3
DG
内错角相等,两直线平行
110°
两直线平行,同旁内角互补
A
B
C
∟
∟
D
G
E
1
2
3
14.如图,已知AD⊥BC,EG⊥BC,垂足分别为D,G,又∠GEC=∠3, 那么AD平分∠BAC吗?为什么?
解:
AD平分∠BAC.
∵ AD⊥BC,EG⊥BC,
∴ AD∥EG.
∴∠2=∠3,
∵∠GEC=∠3,
∠1=∠GEC,
∴∠1=∠2.
∴AD平分∠BAC.
三.解答题
15.如图,已知∠1=∠BDC, ∠2+∠3=180°.
(1) AD∥EC吗?请说明理由.
(2) 已知DA平分∠BDC , CE⊥AE于点E,
∠1=70°,求∠FAB的度数.
解:
AD∥EC.
(1)
理由如下:
∵∠1=∠BDC,
∴ AB∥CD.
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴ ∠ADC+∠3=180°.
∴ AD∥EC.
D
1
A
B
C
∟
F
2
3
E
15.如图,已知∠1=∠BDC, ∠2+∠3=180°.
(2) 已知DA平分∠BDC , CE⊥AE于点E,
∠1=70°,求∠FAB的度数.
D
1
A
B
C
∟
F
2
3
E
(2)
∠1=70°,
=55°.
∴∠ADC= ∠BDC
=90°-35°
∴ ∠FAD=∠AEC=90°.
∵ AD∥EC,
∵DA平分∠BDC ,
∴∠FAB=∠FAD-∠2
∵CE⊥AE,
∴∠AEC=90°.
1
2
= ∠1= ×70°
=35°,
1
2
1
2
16.如图,将方格中的“机器人”图形向右平移3格 ;再向下平移3格,在方格中画出平移后得到的图形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
