第二章气体、液体和固体复习课课件-2021-2022学年高二下学期物理粤教版(2019)选择性必修第三册(共49张ppt)
文档属性
| 名称 | 第二章气体、液体和固体复习课课件-2021-2022学年高二下学期物理粤教版(2019)选择性必修第三册(共49张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览







文档简介
(共49张PPT)
气体液体固体单元复习
高二—粤教版—物理—选择性必修三第二章
基础知识
一、气体
(一)气体实验定律
(二)理想气体状态方程
玻意耳定律
查理定律
盖-吕萨克定律
(一)气体实验定律
描述气体的状态参量有三个:压强、体积、温度。我们通过实验研究它们之间的关系时,需要采用控制变量法进行研究。
1.玻意耳定律(等温过程)
(一)气体实验定律
将一段气体封闭在注射器中,缓慢向下压或向上提注射器的柱塞,观察空气柱体积和压力表所示的压强变化。
1.玻意耳定律(等温过程)
(1)内容:
一定质量的某种气体,在温度不变的情况下,压强与体积成反比。
(2)表达式:
(一)气体实验定律
1.玻意耳定律(等温过程)
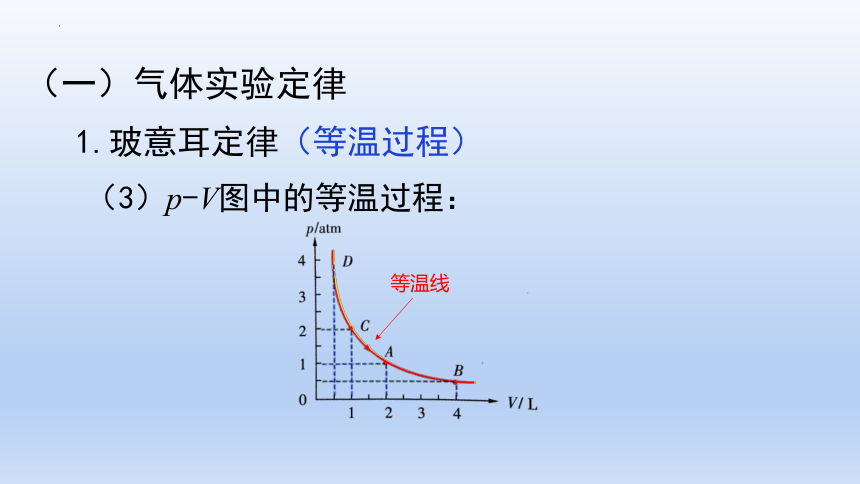
(3)p-V图中的等温过程:
(一)气体实验定律
等温线
2.查理定律(等容过程)
(一)气体实验定律
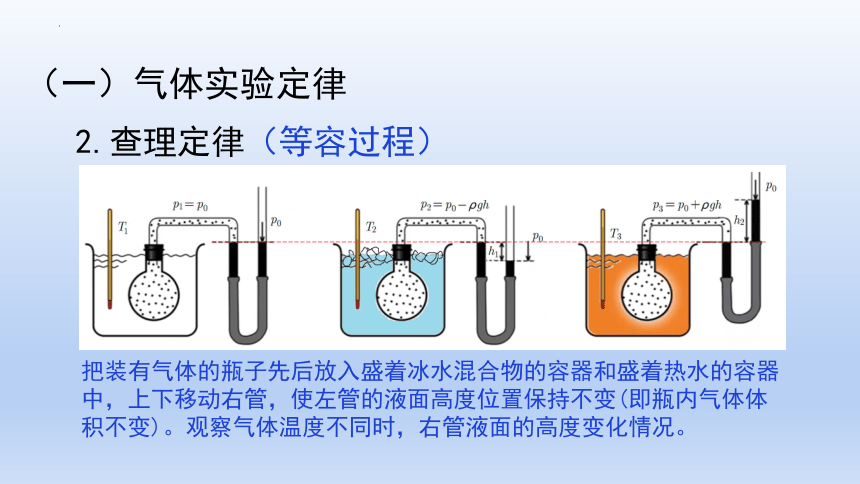
把装有气体的瓶子先后放入盛着冰水混合物的容器和盛着热水的容器中,上下移动右管,使左管的液面高度位置保持不变(即瓶内气体体积不变)。观察气体温度不同时,右管液面的高度变化情况。
2.查理定律(等容过程)
(1)内容:
一定质量的某种气体,在体积不变的情况下,压强与热力学温度成正比。
(2)表达式:
(一)气体实验定律
2.查理定律(等容过程)
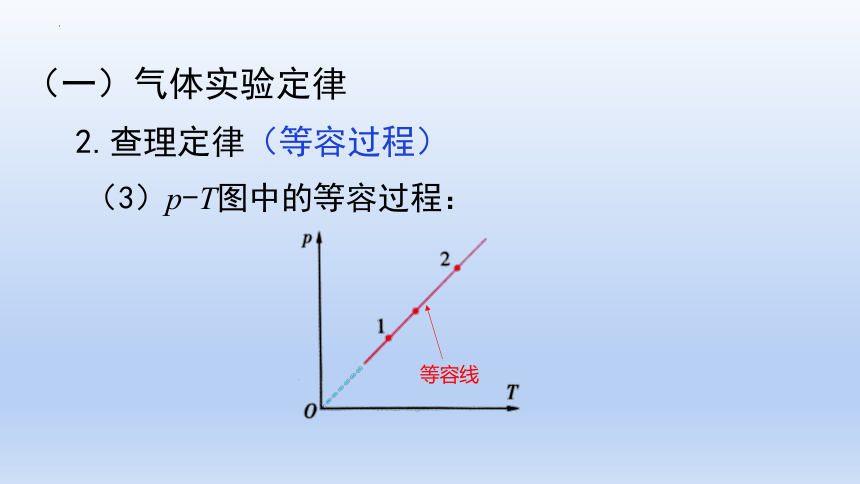
(3)p-T图中的等容过程:
(一)气体实验定律
等容线
3.盖-吕萨克定律(等压过程)
(一)气体实验定律
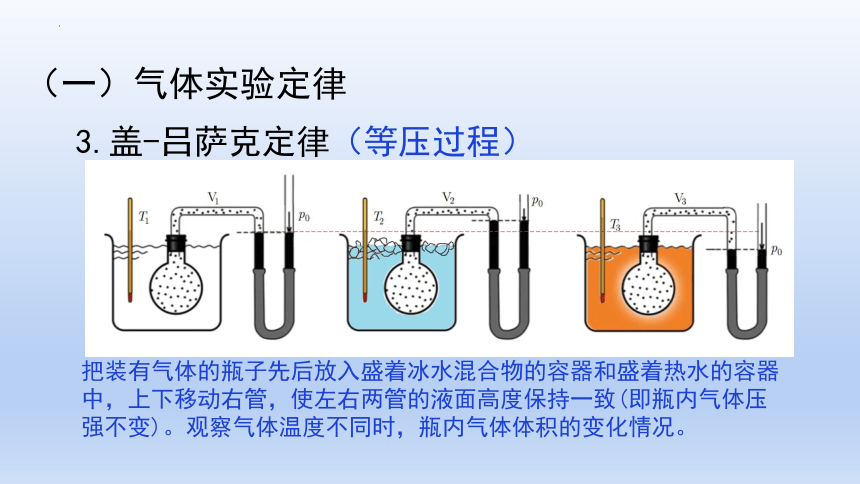
把装有气体的瓶子先后放入盛着冰水混合物的容器和盛着热水的容器中,上下移动右管,使左右两管的液面高度保持一致(即瓶内气体压强不变)。观察气体温度不同时,瓶内气体体积的变化情况。
3.盖-吕萨克定律(等压过程)
(1)内容:
一定质量的某种气体,在压强不变的情况下,体积与热力学温度成正比。
(2)表达式:
(一)气体实验定律
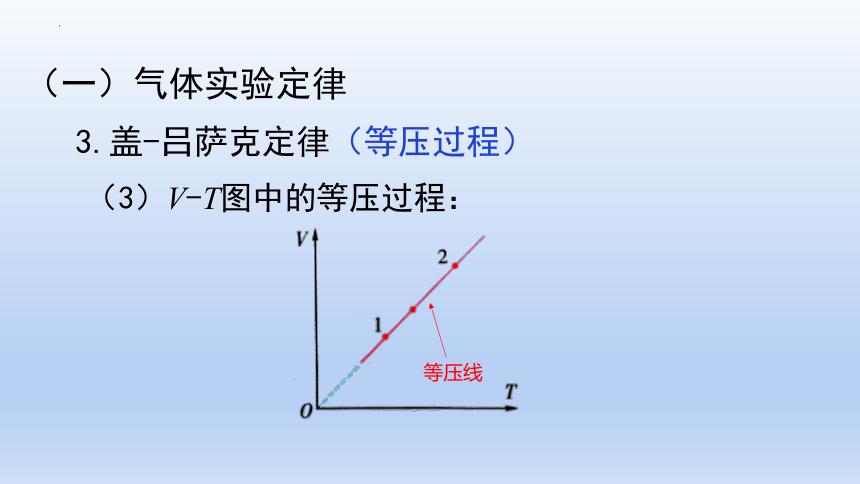
3.盖-吕萨克定律(等压过程)
(3)V-T图中的等压过程:
(一)气体实验定律
等压线
玻意耳定律、查理定律和盖-吕萨克定律,这三个定律都是通过实验研究获得的,它们统称为气体实验定律。它们反应了一定质量的气体的温度、体积、压强三个参量之间的变化关系。
(一)气体实验定律
(一)气体实验定律
4.气体实验定律的微观解释
气体的压强是大量气体分子频繁碰撞器壁的结果。
影响气体压强的两个因素是:
① 气体分子热运动的平均速率
② 气体分子的密集程度
(1)玻意耳定律的微观解释:
一定质量的气体,温度保持不变时,分子热运动的平均速率不变。这种情况下:
4.气体实验定律的微观解释
若气体体积减小,分子密集程度增大,气体压强增大;
若气体体积增大,分子密集程度减小,气体压强减小。
(2)查理定律的微观解释:
一定质量的某种气体,体积保持不变时,分子的密集程度不变。这种情况下:
4.气体实验定律的微观解释
若温度升高,分子热运动的平均速率增大,气体压强增大;
若温度降低,分子热运动的平均速率减小,气体压强减小。
(3)盖-吕萨克定律的微观解释:
一定质量的某种气体,要使压强保持不变:
当温度升高时,由于气体分子热运动的平均速率增大,必须同时增大气体体积,使分子的密集程度减小;
当温度降低时,由于气体分子热运动的平均速率减小,必须同时减小气体体积,使分子的密集程度增大。
4.气体实验定律的微观解释
在对气体实验定律的进一步精确实验研究中可以发现,任何实际气体都只是在压强不太大、温度不太低的情况下近似地遵循相关的定律。当压强较大、温度很低时,气体实验定律就不适用了。
虽然实际气体不严格遵循气体实验定律,但为了研究方便,我们可以设想有一种严格遵循气体实验定律的气体,这样的气体被称为理想气体。
(二)理想气体状态方程
对于一定质量的理想气体,其压强、体积、热力学温度之间满足以下关系:
基础知识
应用气体实验定律或理想气体状态方程解题的思路:
① 确定研究对象;
② 找到p、V、T三个参量的初末状态;
③ 明确变化过程的特点;
④ 列出方程。
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(1)现对密闭气体加热,当温度升到400K,其压强多大?
(2)若在此时拔去销子K,活塞开始向上运动,
当它最后静止在某一位置时,汽缸内气体的温度
为360K,则这时活塞离缸底的距离为多少?
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(1)现对密闭气体加热,当温度升到400K,其压强多大?
加热过程缸内气体的体积不变,为等容变化过程。
初状态气体的压强p1=1.5×105Pa,温度T1=300K;
末状态气体的压强设为p2,温度T2=400K.
对缸内气体,由查理定律得:
解得p2=2.0×105Pa.
活塞最后静止,设此时缸内气体的压强为p3,
对活塞作受力分析,根据平衡条件有:p0S+mg=p3S
解得p3=1.2×105Pa.
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,汽缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
p0S
p3S
mg
设最后静止时活塞离缸底的距离为h3,以缸内气体为研究对象,
初状态气体的压强p1=1.5×105Pa,
体积V1=Sh1=1.2×10-4m3,温度T1=300K;
末状态气体的压强p3=1.2×105Pa,
体积V3=Sh3,温度T3=360K;
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,汽缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
h3
由理想气体状态方程得:
解得h3=18cm.
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,汽缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
h3
例2:(多选)如图为一定质量的理想气体两次在不同体积下的等容变化图线,有关说法正确的是( )
A.a点对应的气体分子密集程度大于b点对应的气体分子密集程度
B.a点对应的气体状态其体积等于b点对应的气体体积
C.由状态a沿直线ab到状态b,气体经历的是等容过程
D.由状态a沿直线ab到状态b,气体经历的是等温过程
AD
基础知识
二、液体
(一)表面张力
(二)浸润与不浸润
(三)毛细现象
(一)表面张力:
由于液体表面层中的分子相互吸引而使液体表面具有收缩趋势的张力。
1.形成原因:
液体表面层的分子分布比液体内部稀疏,分子间距大于平衡距离,分子间相互吸引形成张力。
(一)表面张力:
2.表面张力的方向:
和液面相切,垂直于液面上的各条分界线。
3.表面张力的效果:
表面张力使液体表面具有收缩趋势,使液体表面积趋于最小。
(一)表面张力:
1.形成原因:
附着层内的分子因受液体或固体分子力情况的不同,造成附着层具有收缩或扩张趋势。
(二)浸润与不浸润
2.分类:
①浸润:液体与固体接触时,液体附着在固体上且接触面有扩张趋势。
(二)浸润与不浸润
②不浸润:液体与固体接触时,液体不附着在固体上且接触面有收缩趋势。
浸润液体在毛细管中上升,不浸润液体在毛细管中下降的现象。
形成原因:毛细现象是液体的浸润(或不浸润)与表面张力现象共同作用的结果。
(三)毛细现象:
例3:(多选)下列说法中正确的是( )
A.图甲所示,雨水没有透过布雨伞是因为液体表面存在张力
B.图乙所示,夏天荷叶上小水珠呈球状是由于液体表面张力使其表面积具有收缩到最小趋势的缘故
C.液体分子的热运动没有长期固定的平衡位置
D.图丙所示,小木块能够浮于水面上是液体表面张力与其重力平衡的结果
ABC
例4:(多选)对于液体在器壁附近的液面发生弯曲的现象,如图甲、乙所示。对此有下列几种解释,正确的是( )
A.表面层I内分子的分布比液体内部疏
B.表面层II内分子的分布比液体内部密
C.附着层I内分子的分布比液体内部密
D.附着层II内分子的分布比液体内部疏
ACD
基础知识
三、固体
(一)分类
晶体
非晶体
单晶体
多晶体
三、固体
(二)特点
晶体 非晶体
单晶体 多晶体
几何形状 规则 不规则 不规则
熔点 确定 不确定
物理性质 各向异性 各向同性
三、固体
在不同条件下,同种物质的微粒在空间按不同的规则排列,可以生成不同的晶体。
碳原子按图(a)方式排列就成为金刚石,按图(b)方式排列就成为石墨。
例5:甲、乙、丙三种固体薄片上涂上石蜡,由烧热的针接触其上一点,石蜡熔化的范围如图甲、乙、丙所示,而甲、乙、丙三种固体在熔化过程中温度随加热时间变化的关系如图丁所示,下列说法正确的是( )
A.甲、乙为非晶体,丙是晶体
B.甲、乙、丙都是晶体
C.甲、丙为非晶体,乙是晶体
D.甲为多晶体,乙为非晶体,丙为单晶体
D
课堂总结
气体、固体、液体
气体
气体实验定律
理想气体状态方程
液体
表面张力
毛细现象
浸润与不浸润
固体:单晶体、多晶体、非晶体的特点
练习1:(多选)下列现象中,与液体表面张力有关的是( )
A.小缝衣针漂浮在水面上
B.小木船漂浮在水面上
C.荷叶上的小水珠呈球形
D.慢慢向小酒杯中注水,即使水面稍高出杯口,水仍不会流下来
ACD
问题1:区分表面张力与浮力
如何判断物体浮于水面是表面张力在起作用还是浮力在起作用?
表面张力
浮力
问题1:区分表面张力与浮力
a→b:等压变化,V减小,T减小
b→c:等温变化,p减小,V增大
c→a:等容变化,p增大,T增大
练习2:某种理想气体从状态a变化到状态b,再变化到状态c,最后回到状态a,如图所示是该过程的 p-V 图像,已知图中bc曲线为一条等温线,请画出全过程对应的 p-T 图像和 V-T 图像。
问题2:p-V 图、 p-T 图和 V-T 图的相互转化
问题2:p-V 图、 p-T 图和 V-T 图的相互转化
a
b
c
(c与a体积相等)
a→b:等压变化,V减小,T减小
b→c:等温变化,p减小,V增大
c→a:等容变化,p增大,T增大
问题2:p-V 图、 p-T 图和 V-T 图的相互转化
a
c
b
(a与b压强相等)
(c与a体积相等)
a→b:等压变化,V减小,T减小
b→c:等温变化,p减小,V增大
c→a:等容变化,p增大,T增大
练习3:课本28页练习1
如图所示,一个敞口的瓶子被放在空气中,气温为27℃。现对瓶子加热,由于瓶子中的空气受热膨胀,一部分气体被排出。当瓶子中空气的温度上升到57℃时,瓶子中剩余空气的质量是原来的多少?
问题3:变质量气体问题的处理
问题3:变质量气体问题的处理
关键:变质量→定质量
想象用一个大口袋把瓶内剩余的空气与排出的空气都装在里面。
此时口袋内的所有空气可以看作一个整体,加热膨胀前后袋内空气的质量不变。
问题3:变质量气体问题的处理
假设被排出的空气体积为V,瓶内剩余的空气体积为V0,加热前瓶中原有气体的质量为m0,加热后瓶中剩余的空气质量为m剩.
由盖-吕萨克定律可得:
已知T1=27℃=300K,T2=57℃=330K,
T1 T2
解得
问题3:变质量气体问题的处理
由于瓶中剩余的空气质量与总质量之间满足:
故瓶中剩余的空气的质量是原来的
T1 T2
气体液体固体单元复习
高二—粤教版—物理—选择性必修三第二章
基础知识
一、气体
(一)气体实验定律
(二)理想气体状态方程
玻意耳定律
查理定律
盖-吕萨克定律
(一)气体实验定律
描述气体的状态参量有三个:压强、体积、温度。我们通过实验研究它们之间的关系时,需要采用控制变量法进行研究。
1.玻意耳定律(等温过程)
(一)气体实验定律
将一段气体封闭在注射器中,缓慢向下压或向上提注射器的柱塞,观察空气柱体积和压力表所示的压强变化。
1.玻意耳定律(等温过程)
(1)内容:
一定质量的某种气体,在温度不变的情况下,压强与体积成反比。
(2)表达式:
(一)气体实验定律
1.玻意耳定律(等温过程)
(3)p-V图中的等温过程:
(一)气体实验定律
等温线
2.查理定律(等容过程)
(一)气体实验定律
把装有气体的瓶子先后放入盛着冰水混合物的容器和盛着热水的容器中,上下移动右管,使左管的液面高度位置保持不变(即瓶内气体体积不变)。观察气体温度不同时,右管液面的高度变化情况。
2.查理定律(等容过程)
(1)内容:
一定质量的某种气体,在体积不变的情况下,压强与热力学温度成正比。
(2)表达式:
(一)气体实验定律
2.查理定律(等容过程)
(3)p-T图中的等容过程:
(一)气体实验定律
等容线
3.盖-吕萨克定律(等压过程)
(一)气体实验定律
把装有气体的瓶子先后放入盛着冰水混合物的容器和盛着热水的容器中,上下移动右管,使左右两管的液面高度保持一致(即瓶内气体压强不变)。观察气体温度不同时,瓶内气体体积的变化情况。
3.盖-吕萨克定律(等压过程)
(1)内容:
一定质量的某种气体,在压强不变的情况下,体积与热力学温度成正比。
(2)表达式:
(一)气体实验定律
3.盖-吕萨克定律(等压过程)
(3)V-T图中的等压过程:
(一)气体实验定律
等压线
玻意耳定律、查理定律和盖-吕萨克定律,这三个定律都是通过实验研究获得的,它们统称为气体实验定律。它们反应了一定质量的气体的温度、体积、压强三个参量之间的变化关系。
(一)气体实验定律
(一)气体实验定律
4.气体实验定律的微观解释
气体的压强是大量气体分子频繁碰撞器壁的结果。
影响气体压强的两个因素是:
① 气体分子热运动的平均速率
② 气体分子的密集程度
(1)玻意耳定律的微观解释:
一定质量的气体,温度保持不变时,分子热运动的平均速率不变。这种情况下:
4.气体实验定律的微观解释
若气体体积减小,分子密集程度增大,气体压强增大;
若气体体积增大,分子密集程度减小,气体压强减小。
(2)查理定律的微观解释:
一定质量的某种气体,体积保持不变时,分子的密集程度不变。这种情况下:
4.气体实验定律的微观解释
若温度升高,分子热运动的平均速率增大,气体压强增大;
若温度降低,分子热运动的平均速率减小,气体压强减小。
(3)盖-吕萨克定律的微观解释:
一定质量的某种气体,要使压强保持不变:
当温度升高时,由于气体分子热运动的平均速率增大,必须同时增大气体体积,使分子的密集程度减小;
当温度降低时,由于气体分子热运动的平均速率减小,必须同时减小气体体积,使分子的密集程度增大。
4.气体实验定律的微观解释
在对气体实验定律的进一步精确实验研究中可以发现,任何实际气体都只是在压强不太大、温度不太低的情况下近似地遵循相关的定律。当压强较大、温度很低时,气体实验定律就不适用了。
虽然实际气体不严格遵循气体实验定律,但为了研究方便,我们可以设想有一种严格遵循气体实验定律的气体,这样的气体被称为理想气体。
(二)理想气体状态方程
对于一定质量的理想气体,其压强、体积、热力学温度之间满足以下关系:
基础知识
应用气体实验定律或理想气体状态方程解题的思路:
① 确定研究对象;
② 找到p、V、T三个参量的初末状态;
③ 明确变化过程的特点;
④ 列出方程。
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(1)现对密闭气体加热,当温度升到400K,其压强多大?
(2)若在此时拔去销子K,活塞开始向上运动,
当它最后静止在某一位置时,汽缸内气体的温度
为360K,则这时活塞离缸底的距离为多少?
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(1)现对密闭气体加热,当温度升到400K,其压强多大?
加热过程缸内气体的体积不变,为等容变化过程。
初状态气体的压强p1=1.5×105Pa,温度T1=300K;
末状态气体的压强设为p2,温度T2=400K.
对缸内气体,由查理定律得:
解得p2=2.0×105Pa.
活塞最后静止,设此时缸内气体的压强为p3,
对活塞作受力分析,根据平衡条件有:p0S+mg=p3S
解得p3=1.2×105Pa.
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,汽缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
p0S
p3S
mg
设最后静止时活塞离缸底的距离为h3,以缸内气体为研究对象,
初状态气体的压强p1=1.5×105Pa,
体积V1=Sh1=1.2×10-4m3,温度T1=300K;
末状态气体的压强p3=1.2×105Pa,
体积V3=Sh3,温度T3=360K;
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,汽缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
h3
由理想气体状态方程得:
解得h3=18cm.
例1:如图所示,足够长的圆柱形汽缸竖直放置,其横截面积为1×10-3m2,汽缸内有质量m=2kg的活塞,活塞与汽缸壁封闭良好,不计摩擦。开始时活塞被销子K销于如图位置,离缸底12cm,此时汽缸内被封闭气体的压强1.5×105Pa,温度为300K。外界大气压为1.0×105Pa,g取10m/s2.
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,汽缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
h3
例2:(多选)如图为一定质量的理想气体两次在不同体积下的等容变化图线,有关说法正确的是( )
A.a点对应的气体分子密集程度大于b点对应的气体分子密集程度
B.a点对应的气体状态其体积等于b点对应的气体体积
C.由状态a沿直线ab到状态b,气体经历的是等容过程
D.由状态a沿直线ab到状态b,气体经历的是等温过程
AD
基础知识
二、液体
(一)表面张力
(二)浸润与不浸润
(三)毛细现象
(一)表面张力:
由于液体表面层中的分子相互吸引而使液体表面具有收缩趋势的张力。
1.形成原因:
液体表面层的分子分布比液体内部稀疏,分子间距大于平衡距离,分子间相互吸引形成张力。
(一)表面张力:
2.表面张力的方向:
和液面相切,垂直于液面上的各条分界线。
3.表面张力的效果:
表面张力使液体表面具有收缩趋势,使液体表面积趋于最小。
(一)表面张力:
1.形成原因:
附着层内的分子因受液体或固体分子力情况的不同,造成附着层具有收缩或扩张趋势。
(二)浸润与不浸润
2.分类:
①浸润:液体与固体接触时,液体附着在固体上且接触面有扩张趋势。
(二)浸润与不浸润
②不浸润:液体与固体接触时,液体不附着在固体上且接触面有收缩趋势。
浸润液体在毛细管中上升,不浸润液体在毛细管中下降的现象。
形成原因:毛细现象是液体的浸润(或不浸润)与表面张力现象共同作用的结果。
(三)毛细现象:
例3:(多选)下列说法中正确的是( )
A.图甲所示,雨水没有透过布雨伞是因为液体表面存在张力
B.图乙所示,夏天荷叶上小水珠呈球状是由于液体表面张力使其表面积具有收缩到最小趋势的缘故
C.液体分子的热运动没有长期固定的平衡位置
D.图丙所示,小木块能够浮于水面上是液体表面张力与其重力平衡的结果
ABC
例4:(多选)对于液体在器壁附近的液面发生弯曲的现象,如图甲、乙所示。对此有下列几种解释,正确的是( )
A.表面层I内分子的分布比液体内部疏
B.表面层II内分子的分布比液体内部密
C.附着层I内分子的分布比液体内部密
D.附着层II内分子的分布比液体内部疏
ACD
基础知识
三、固体
(一)分类
晶体
非晶体
单晶体
多晶体
三、固体
(二)特点
晶体 非晶体
单晶体 多晶体
几何形状 规则 不规则 不规则
熔点 确定 不确定
物理性质 各向异性 各向同性
三、固体
在不同条件下,同种物质的微粒在空间按不同的规则排列,可以生成不同的晶体。
碳原子按图(a)方式排列就成为金刚石,按图(b)方式排列就成为石墨。
例5:甲、乙、丙三种固体薄片上涂上石蜡,由烧热的针接触其上一点,石蜡熔化的范围如图甲、乙、丙所示,而甲、乙、丙三种固体在熔化过程中温度随加热时间变化的关系如图丁所示,下列说法正确的是( )
A.甲、乙为非晶体,丙是晶体
B.甲、乙、丙都是晶体
C.甲、丙为非晶体,乙是晶体
D.甲为多晶体,乙为非晶体,丙为单晶体
D
课堂总结
气体、固体、液体
气体
气体实验定律
理想气体状态方程
液体
表面张力
毛细现象
浸润与不浸润
固体:单晶体、多晶体、非晶体的特点
练习1:(多选)下列现象中,与液体表面张力有关的是( )
A.小缝衣针漂浮在水面上
B.小木船漂浮在水面上
C.荷叶上的小水珠呈球形
D.慢慢向小酒杯中注水,即使水面稍高出杯口,水仍不会流下来
ACD
问题1:区分表面张力与浮力
如何判断物体浮于水面是表面张力在起作用还是浮力在起作用?
表面张力
浮力
问题1:区分表面张力与浮力
a→b:等压变化,V减小,T减小
b→c:等温变化,p减小,V增大
c→a:等容变化,p增大,T增大
练习2:某种理想气体从状态a变化到状态b,再变化到状态c,最后回到状态a,如图所示是该过程的 p-V 图像,已知图中bc曲线为一条等温线,请画出全过程对应的 p-T 图像和 V-T 图像。
问题2:p-V 图、 p-T 图和 V-T 图的相互转化
问题2:p-V 图、 p-T 图和 V-T 图的相互转化
a
b
c
(c与a体积相等)
a→b:等压变化,V减小,T减小
b→c:等温变化,p减小,V增大
c→a:等容变化,p增大,T增大
问题2:p-V 图、 p-T 图和 V-T 图的相互转化
a
c
b
(a与b压强相等)
(c与a体积相等)
a→b:等压变化,V减小,T减小
b→c:等温变化,p减小,V增大
c→a:等容变化,p增大,T增大
练习3:课本28页练习1
如图所示,一个敞口的瓶子被放在空气中,气温为27℃。现对瓶子加热,由于瓶子中的空气受热膨胀,一部分气体被排出。当瓶子中空气的温度上升到57℃时,瓶子中剩余空气的质量是原来的多少?
问题3:变质量气体问题的处理
问题3:变质量气体问题的处理
关键:变质量→定质量
想象用一个大口袋把瓶内剩余的空气与排出的空气都装在里面。
此时口袋内的所有空气可以看作一个整体,加热膨胀前后袋内空气的质量不变。
问题3:变质量气体问题的处理
假设被排出的空气体积为V,瓶内剩余的空气体积为V0,加热前瓶中原有气体的质量为m0,加热后瓶中剩余的空气质量为m剩.
由盖-吕萨克定律可得:
已知T1=27℃=300K,T2=57℃=330K,
T1 T2
解得
问题3:变质量气体问题的处理
由于瓶中剩余的空气质量与总质量之间满足:
故瓶中剩余的空气的质量是原来的
T1 T2
同课章节目录
- 第一章 分子动理论
- 第一节 物质是由大量分子组成的
- 第二节 分子热运动与分子力
- 第三节 气体分子运动的统计规律
- 第二章 气体、液体和固态
- 第一节 气体实验定律(Ⅰ)
- 第二节 气体实验定律(Ⅱ)
- 第三节 气体实验定律的微观解释
- 第四节 液体的表面张力
- 第五节 晶体
- 第六节 新材料
- 第三章 热力学定律
- 第一节 热力学第一定律
- 第二节 能量守恒定律及其应用
- 第三节 热力学第二定律
- 第四章 波粒二象性
- 第一节 光电效应
- 第二节 光电效应方程及其意义
- 第三节 光的波粒二象性
- 第四节 德布罗意波
- 第五节 不确定性关系
- 第五章 原子与原子核
- 第一节 原子的结构
- 第二节 放射性元素的衰变
- 第三节 核力与核反应方程
- 第四节 放射性同位素
- 第五节 裂变和聚变
