沪科版数学八年级下册 17.4 一元二次方程的根与系数的关系课件(共17张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 17.4 一元二次方程的根与系数的关系课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览



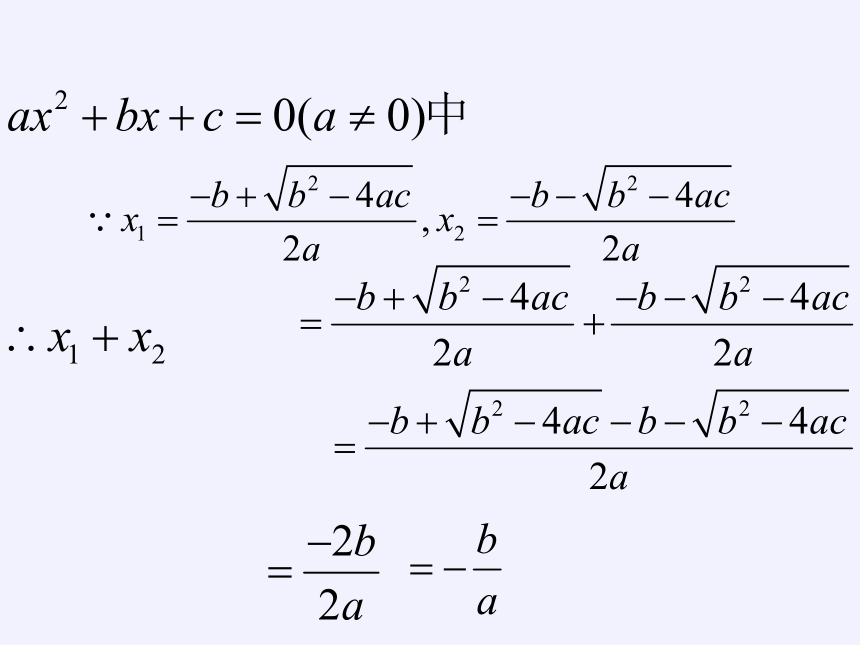
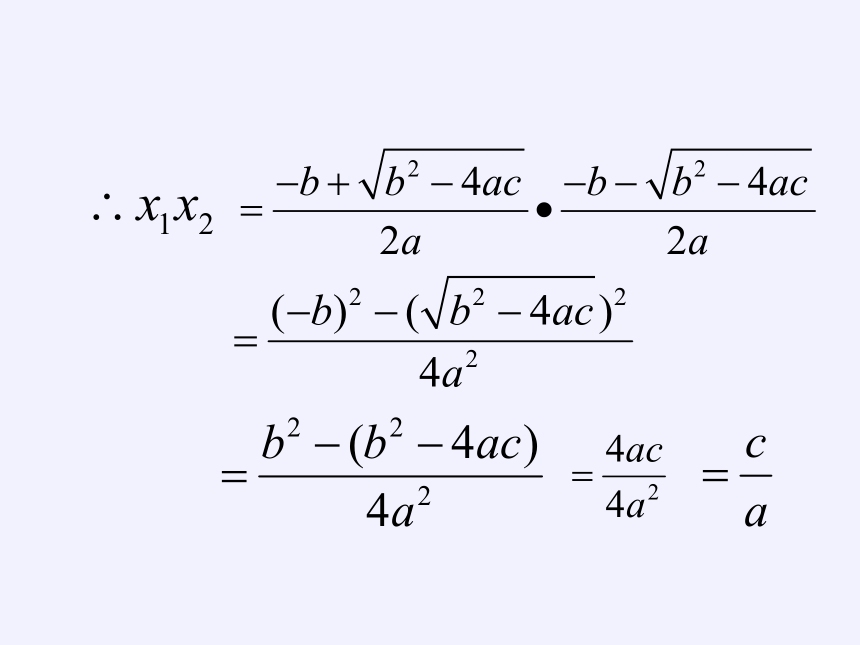
文档简介
(共17张PPT)
17.4 一元二次方程的根与系数的关系
2.求根公式是什么?根的情况怎么确定的?
复习引入
1.一元二次方程的解法有哪些
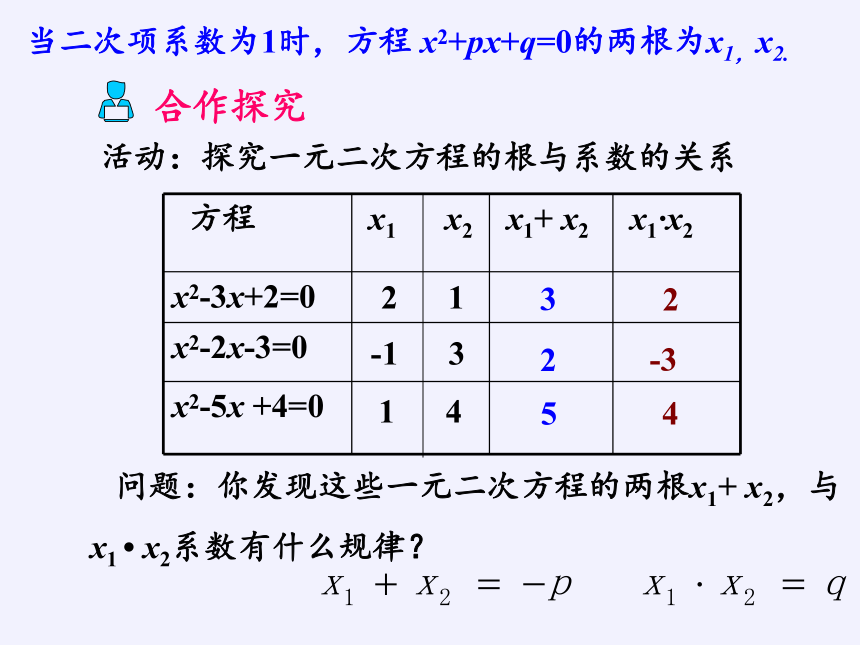
方程 x1 x2 x1+ x2 x1 x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
问题:你发现这些一元二次方程的两根x1+ x2,与x1 x2系数有什么规律?
2 1
-1 3
1 4
3
2
2
-3
5
4
合作探究
活动:探究一元二次方程的根与系数的关系
当二次项系数为1时,方程 x2+px+q=0的两根为x1,x2.
方 程
-2
x1+ x2,x1 x2与系数有什么规律
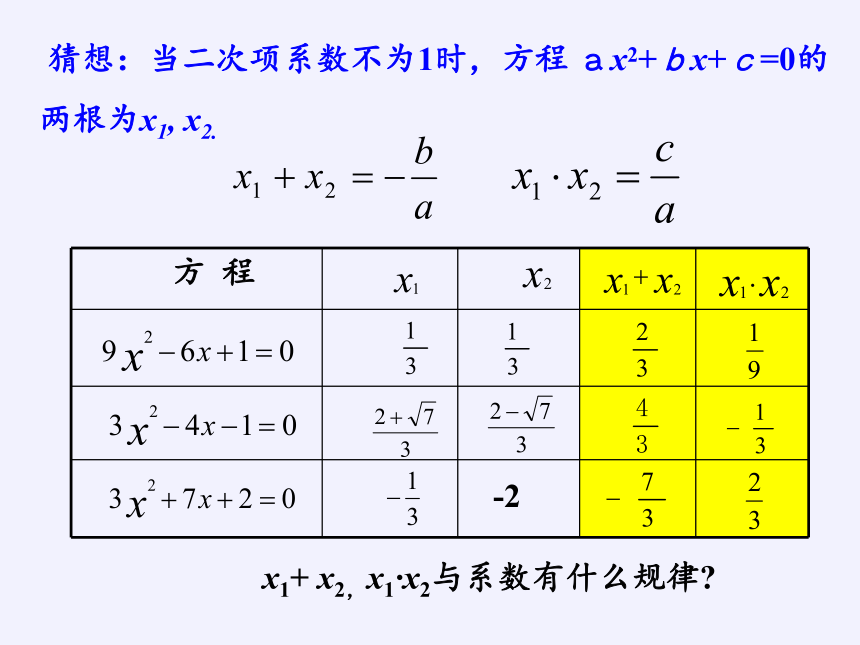
猜想:当二次项系数不为1时,方程 ax2+bx+c=0的两根为x1, x2.
猜想:
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
任何一个一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1 、x2 ,
那么x1 + x2= , x1 ·x2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
一、直接运用根与系数的关系
例1.不解方程,求下列方程两根的和与积.
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用x1+x2=- 时,注意“- ”不要漏写.
二、求关于两根的对称式或代数式的值
例2.设 是方程 的两个根,利用根与系数的关系,求下列各式的值.
三、构造新方程
例3.求一个一元二次方程,使它的两个根是2和3,且二次项系数为1.
变式:且二次项系数为5.
例4.方程 的两根同为正数,求p、q的取值范围.
四、求方程中的待定系数
变式:方程 有一个正根,一个负根,求m的取值范围.
解:由已知,
△=
即
m>0
m-1<0
∴0一正根,一负根
△>0
x1x2<0
两个正根
△≥0
x1x2>0
x1+x2>0
两个负根
△≥0
x1x2>0
x1+x2<0
一元二次方程根与系数的关系?
注:能用根与系数的关系的前提条件为b2-4ac≥0.
课堂小结
谢 谢
17.4 一元二次方程的根与系数的关系
2.求根公式是什么?根的情况怎么确定的?
复习引入
1.一元二次方程的解法有哪些
方程 x1 x2 x1+ x2 x1 x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
问题:你发现这些一元二次方程的两根x1+ x2,与x1 x2系数有什么规律?
2 1
-1 3
1 4
3
2
2
-3
5
4
合作探究
活动:探究一元二次方程的根与系数的关系
当二次项系数为1时,方程 x2+px+q=0的两根为x1,x2.
方 程
-2
x1+ x2,x1 x2与系数有什么规律
猜想:当二次项系数不为1时,方程 ax2+bx+c=0的两根为x1, x2.
猜想:
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
任何一个一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1 、x2 ,
那么x1 + x2= , x1 ·x2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
一、直接运用根与系数的关系
例1.不解方程,求下列方程两根的和与积.
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用x1+x2=- 时,注意“- ”不要漏写.
二、求关于两根的对称式或代数式的值
例2.设 是方程 的两个根,利用根与系数的关系,求下列各式的值.
三、构造新方程
例3.求一个一元二次方程,使它的两个根是2和3,且二次项系数为1.
变式:且二次项系数为5.
例4.方程 的两根同为正数,求p、q的取值范围.
四、求方程中的待定系数
变式:方程 有一个正根,一个负根,求m的取值范围.
解:由已知,
△=
即
m>0
m-1<0
∴0
△>0
x1x2<0
两个正根
△≥0
x1x2>0
x1+x2>0
两个负根
△≥0
x1x2>0
x1+x2<0
一元二次方程根与系数的关系?
注:能用根与系数的关系的前提条件为b2-4ac≥0.
课堂小结
谢 谢
