沪科版八年级下册 19.3矩形.菱形.正方形课件(共18张PPT)
文档属性
| 名称 | 沪科版八年级下册 19.3矩形.菱形.正方形课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 06:35:30 | ||
图片预览




文档简介
(共18张PPT)
19.3矩形、菱形、正方形
1.定义:
有两组对边分别平行的四边形
叫做平行四边形.
2.记作:
ABCD
3.读作:平行四边形ABCD
A
B
C
D
巩固复行四边形的性质:
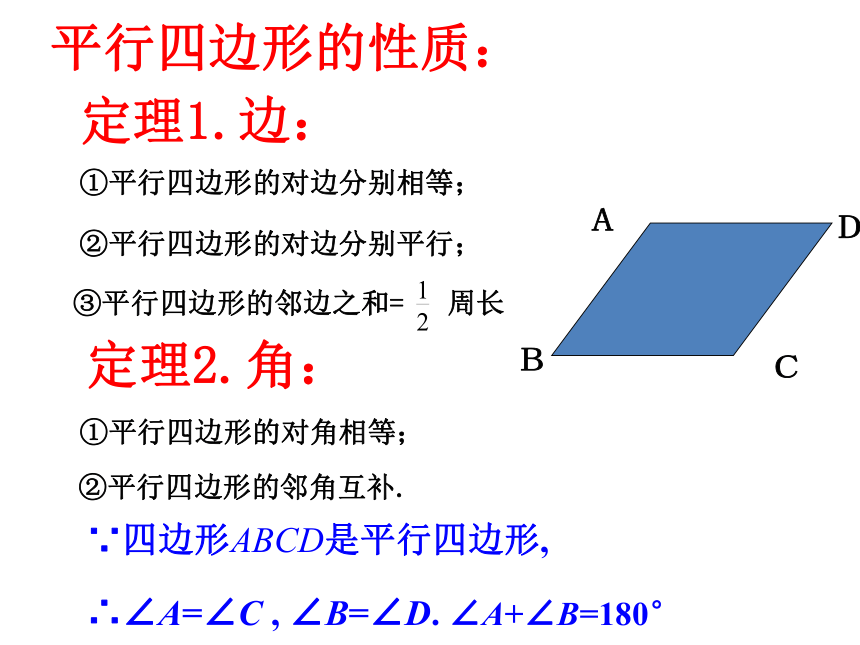
①平行四边形的对边分别相等;
①平行四边形的对角相等;
A
B
C
D
定理1.边:
定理2.角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D. ∠A+∠B=180°
②平行四边形的对边分别平行;
③平行四边形的邻边之和= 周长
②平行四边形的邻角互补.
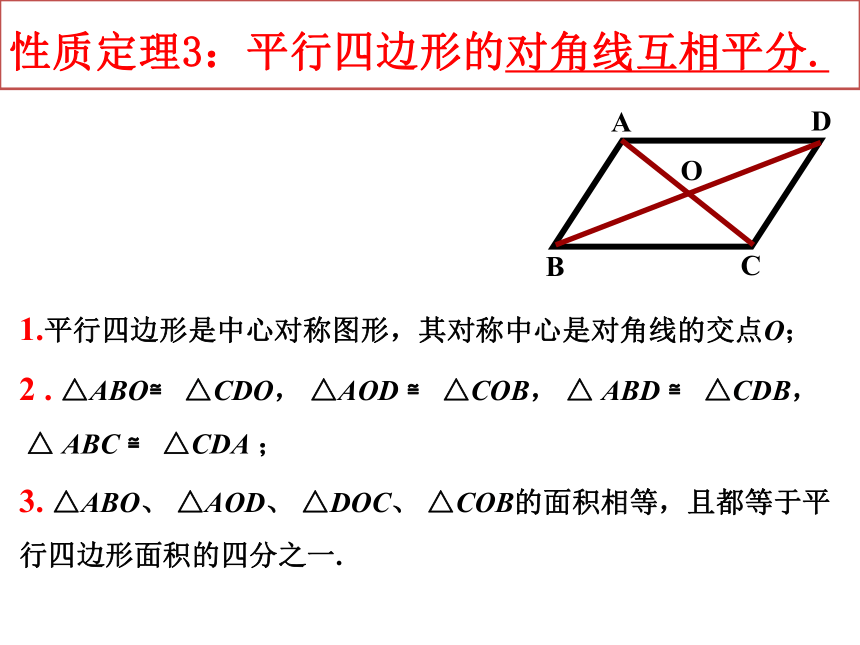
1.平行四边形是中心对称图形,其对称中心是对角线的交点O;
2 . △ABO≌ △CDO, △AOD ≌ △COB, △ ABD ≌ △CDB,
△ ABC ≌ △CDA ;
3. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
A
C
D
B
O
性质定理3:平行四边形的对角线互相平分.
矩形
本节课你将学到……
1、矩形的概念
2、矩形的性质
3、运用性质证明
新课引入
1.矩形的定义:有一个角是直角的平行四边形是矩形
D
A
B
C
D
A
B
C
一个角是直角
2.矩形的表示方法:矩形ABCD
特殊性
1、矩形是一个特殊的平行四边形,具有平行四边形的所有性质,并且还有平行四边形没有的性质。
矩形有哪些性质呢?
2、矩形还有哪些特殊性质呢?
性质1:矩形的对角相等,邻角互补,矩形的四个角都是直角.
证明:∵四边形ABCD是矩形
∴ ∠C=∠A=90°,
∠D= ∠B
AD∥BC
∴ ∠A+ ∠B=180°
∴ ∠D=∠B=180°-∠A
=180°- 90° =90°
即矩形的四个角都是直角.
A
B
C
D
已知:如图,四边形ABCD是矩形,且∠A=90°
求证:∠A= ∠ B= ∠ C= ∠ D=90°
性质2:矩形对角线互相平分,矩形的对角线相等.
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
即矩形的对角线相等.
矩形的对角相等,邻角互补,矩形的四个角都是直角.
矩形的对角线相等且互相平分
从角上看:
从对角线上看:
A
B
C
D
A
B
C
D
从边上看:
矩形的对边平行且相等。
矩 形 的 性 质
O
D
C
A
┛
在Rt△ABD中,AO是斜边BD的中线
则有:AO= BD
在矩形ABCD中
AO=CO=BO=DO= AC= BD
B
推论: 直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
C
B
A
O
例1 如图,矩形ABCD的两条对角线相交于点O,
已知∠BOC=120°,AB=6cm. 求AC的长.
解:
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
10
5
4
练一练
4√3
再攀高峰
3.在矩形ABCD中,AE⊥BD于E,若BE=OE=1,求AC的长。
解:∵BE=OE=1
∴BO=2
∵ABCD是矩形
∴AC=BD=2BO=4
A
B
C
D
O
E
2、矩形的性质定理1:矩形的四个角都是直角
3、矩形的性质定理2:矩形的对角线相等
4、推论:直角三角形斜边上的中线等于斜边的一半.
课堂小结:
1、矩形的定义:有一个角是直角的平行四边形
19.3矩形、菱形、正方形
1.定义:
有两组对边分别平行的四边形
叫做平行四边形.
2.记作:
ABCD
3.读作:平行四边形ABCD
A
B
C
D
巩固复行四边形的性质:
①平行四边形的对边分别相等;
①平行四边形的对角相等;
A
B
C
D
定理1.边:
定理2.角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D. ∠A+∠B=180°
②平行四边形的对边分别平行;
③平行四边形的邻边之和= 周长
②平行四边形的邻角互补.
1.平行四边形是中心对称图形,其对称中心是对角线的交点O;
2 . △ABO≌ △CDO, △AOD ≌ △COB, △ ABD ≌ △CDB,
△ ABC ≌ △CDA ;
3. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
A
C
D
B
O
性质定理3:平行四边形的对角线互相平分.
矩形
本节课你将学到……
1、矩形的概念
2、矩形的性质
3、运用性质证明
新课引入
1.矩形的定义:有一个角是直角的平行四边形是矩形
D
A
B
C
D
A
B
C
一个角是直角
2.矩形的表示方法:矩形ABCD
特殊性
1、矩形是一个特殊的平行四边形,具有平行四边形的所有性质,并且还有平行四边形没有的性质。
矩形有哪些性质呢?
2、矩形还有哪些特殊性质呢?
性质1:矩形的对角相等,邻角互补,矩形的四个角都是直角.
证明:∵四边形ABCD是矩形
∴ ∠C=∠A=90°,
∠D= ∠B
AD∥BC
∴ ∠A+ ∠B=180°
∴ ∠D=∠B=180°-∠A
=180°- 90° =90°
即矩形的四个角都是直角.
A
B
C
D
已知:如图,四边形ABCD是矩形,且∠A=90°
求证:∠A= ∠ B= ∠ C= ∠ D=90°
性质2:矩形对角线互相平分,矩形的对角线相等.
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
即矩形的对角线相等.
矩形的对角相等,邻角互补,矩形的四个角都是直角.
矩形的对角线相等且互相平分
从角上看:
从对角线上看:
A
B
C
D
A
B
C
D
从边上看:
矩形的对边平行且相等。
矩 形 的 性 质
O
D
C
A
┛
在Rt△ABD中,AO是斜边BD的中线
则有:AO= BD
在矩形ABCD中
AO=CO=BO=DO= AC= BD
B
推论: 直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
C
B
A
O
例1 如图,矩形ABCD的两条对角线相交于点O,
已知∠BOC=120°,AB=6cm. 求AC的长.
解:
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
10
5
4
练一练
4√3
再攀高峰
3.在矩形ABCD中,AE⊥BD于E,若BE=OE=1,求AC的长。
解:∵BE=OE=1
∴BO=2
∵ABCD是矩形
∴AC=BD=2BO=4
A
B
C
D
O
E
2、矩形的性质定理1:矩形的四个角都是直角
3、矩形的性质定理2:矩形的对角线相等
4、推论:直角三角形斜边上的中线等于斜边的一半.
课堂小结:
1、矩形的定义:有一个角是直角的平行四边形
