沪科版数学七年级上册同步课时练习:2.1.2 第2课时 代数式的意义及规律探究(word版含答案)
文档属性
| 名称 | 沪科版数学七年级上册同步课时练习:2.1.2 第2课时 代数式的意义及规律探究(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 174.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 14:14:29 | ||
图片预览

文档简介
2.1.2 第2课时 代数式的意义及规律探究
知识点 1 描述代数式的意义
1.下列代数式的意义表示错误的是 ( )
A.2x+3y表示2x与3y的和
B. 表示5x除以2y所得的商
C. 9-y表示9减去y的所得的差
D.a2+b2表示a与b和的平方
2.体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元,则代数式50表示的实际意义是 .
知识点 2 用代数式探究数字规律
3.观察下列有理数:-,-,,-,,-,…,按此规律,第n个有理数是 .(n为正整数)
4.[2019·合肥包河区期中改编] 下列每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为 ( )
A.135 B.170
C.209 D.252
知识点 3 用代数式探究图形规律
5.观察下列图形:
它们是按一定规律排列的,依照此规律,第20个图形共有 个★.
6.[2019·大庆] 归纳“T”字形,用棋子摆成的“T”字形如图示,按照图①,图②,图③的规律摆下去,摆成第n个“T”字形需要的棋子个数为 .
7.某商店举办促销活动,促销的方法是将原价x元的衣服以x-10元出售,则下列说法中,能正确表达该商店促销方法的是( )
A.原价减去10元后再打8折
B.原价打8折后再减去10元
C.原价减去10元后再打2折
D.原价打2折后再减去10元
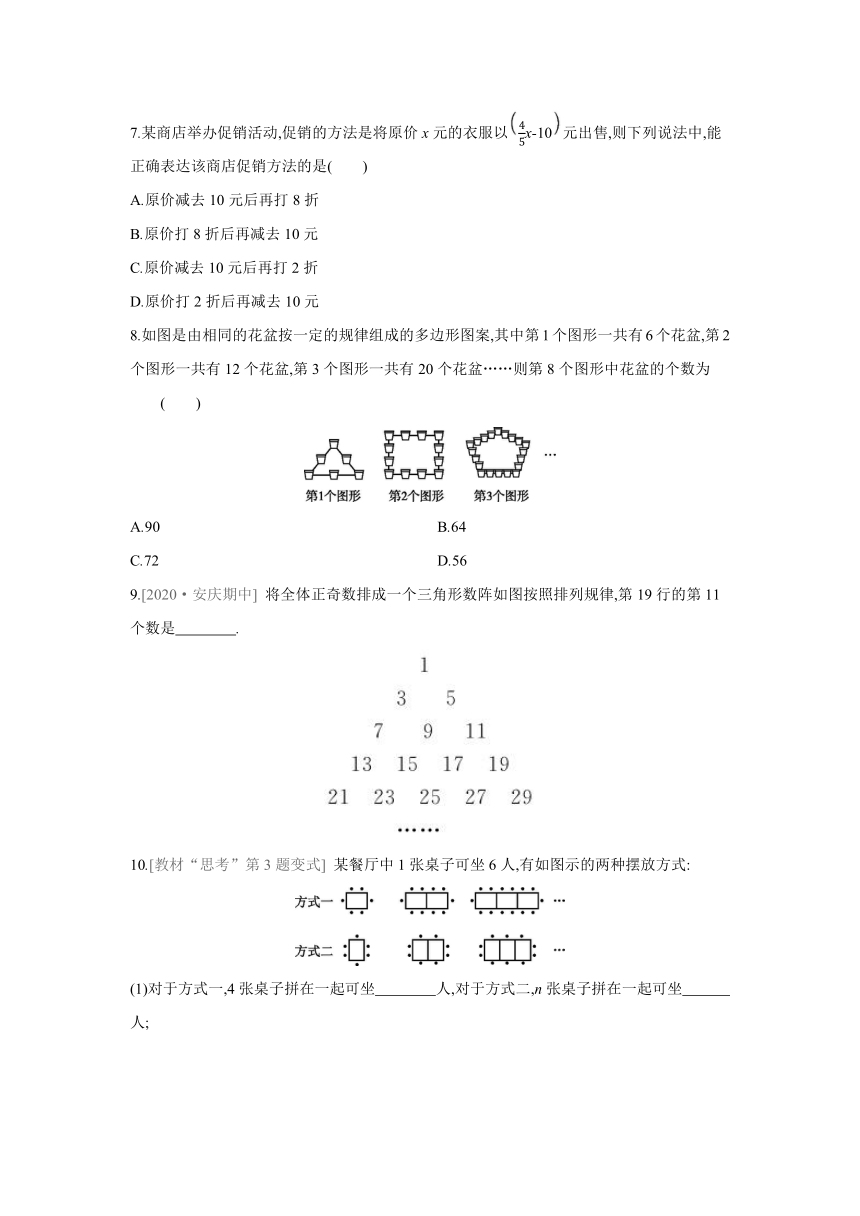
8.如图是由相同的花盆按一定的规律组成的多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆……则第8个图形中花盆的个数为 ( )
A.90 B.64
C.72 D.56
9.[2020·安庆期中] 将全体正奇数排成一个三角形数阵如图按照排列规律,第19行的第11个数是 .
10.[教材“思考”第3题变式] 某餐厅中1张桌子可坐6人,有如图示的两种摆放方式:
(1)对于方式一,4张桌子拼在一起可坐 人,对于方式二,n张桌子拼在一起可坐 人;
(2)该餐厅有30张这样的长方形桌子,由于受场地限制,可按方式一的拼法每5张拼成一张大桌子,或按方式二的拼法每6张拼成一张大桌子,一天中午,该餐厅来了98位顾客共同就餐,若你是这家餐厅的经理,你打算选择方式 来摆放桌子.
答案
1.D A项,2x+3y表示2x与3y的和,说法正确,不符合题意;
B项,表示5x除以2y所得的商,说法正确,不符合题意;
C项,9-y表示9减去y的所得的差,说法正确,不符合题意;
D项,a2+b2表示a的平方与b的平方的和,原来的说法错误,符合题意.故选D.
2.小金买了3个足球、2个篮球后剩余的钱数
3.(-1)n+1 分子依次为-1,1,3,5,7,9,…,相邻两个分子之间相差2,第n个数的分子可以表示为2n-3.
第一个数的分母为2=12+1,
第二个数的分母为5=22+1,
第三个数的分母为10=32+1,
…
所以第n个数的分母为n2+1,
所以第n个有理数是(-1)n+1(n为正整数).
故答案为(-1)n+1.
4.C 首先根据图示,可得第n个表格的左上角的数等于n,左下角的数等于n+1;右上角的数是左下角的数的2倍,右下角的数等于左下角的数与右上角的数的积加上左上角的数,所以a=20,b=10,x=20×10+9=209.
5.68 将图形分为两部分分析,第一行和最后一行都是一个星星,中间是一个方阵,根据第一个图形中间是3×3(个)星星,第二个图形中间是3×4(个)星星,依次类推即可得出答案.
观察图形的变化情况可知:
第1个图形中共有3×3+2=11(个)★;
第2个图形中共有3×4+2=14(个)★;
第3个图形中共有3×5+2=17(个)★;
…
第20个图形中共有3×22+2=68(个)★.
故答案为68.
6.3n+2 由图可得,
图①中棋子的个数为3×1+2=5,
图②中棋子的个数为3×2+2=8,
图③中棋子的个数为3×3+2=11,
……
则第n个“T”字形需要的棋子个数为3n+2.
7.B
8.A 观察图形,得出花盆个数变化的规律作答即可.第1个图形中,三角形每条边上有3个花盆, 共计(32-3)个花盆;第2个图形中,四边形每条边上有4个花盆, 共计(42-4)个花盆;第3个图形中, 五边形每条边上有5个花盆, 共计(52-5)个花盆……第n个图形中,(n+2)边形每条边上有(n+2)个花盆, 共计[(n+2)2-(n+2)]个花盆, 则第8个图形中花盆的个数为(8+2)2-(8+2)=90.故选A.
9.363 观察所给数阵,得每一行的变化规律如下:
第一行的第一个数为1×0+1=1,
第二行的第一个数为2×1+1=3,
第三行的第一个数为3×2+1=7,
…
第n行的第一个数为n(n-1)+1.
所以第19行的第一个数为19×18+1=343,
所以第19行的第11个数为343+10×2=363.
10.(1)18 (2n+4) (2)一
(1)对于方式一:4张桌子拼在一起可坐2+4×4=18(人),
对于方式二,n张桌子拼在一起可坐(2n+4)人.
故答案为18,(2n+4).
(2)按方式一,每5张桌子拼成一张大桌子,则一张大桌子可坐2+4×5=22(人),则30张桌子可拼成6张大桌子,共可坐22×6=132(人).
按方式二,每6张桌子拼成一张大桌子,则一张大桌子可坐2×6+4=16(人),则30张桌子可拼成5张大桌子,共可坐16×5=80(人).
因为132>98>80,所以应该按方式一的拼法摆放桌子.
知识点 1 描述代数式的意义
1.下列代数式的意义表示错误的是 ( )
A.2x+3y表示2x与3y的和
B. 表示5x除以2y所得的商
C. 9-y表示9减去y的所得的差
D.a2+b2表示a与b和的平方
2.体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元,则代数式50表示的实际意义是 .
知识点 2 用代数式探究数字规律
3.观察下列有理数:-,-,,-,,-,…,按此规律,第n个有理数是 .(n为正整数)
4.[2019·合肥包河区期中改编] 下列每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为 ( )
A.135 B.170
C.209 D.252
知识点 3 用代数式探究图形规律
5.观察下列图形:
它们是按一定规律排列的,依照此规律,第20个图形共有 个★.
6.[2019·大庆] 归纳“T”字形,用棋子摆成的“T”字形如图示,按照图①,图②,图③的规律摆下去,摆成第n个“T”字形需要的棋子个数为 .
7.某商店举办促销活动,促销的方法是将原价x元的衣服以x-10元出售,则下列说法中,能正确表达该商店促销方法的是( )
A.原价减去10元后再打8折
B.原价打8折后再减去10元
C.原价减去10元后再打2折
D.原价打2折后再减去10元
8.如图是由相同的花盆按一定的规律组成的多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆……则第8个图形中花盆的个数为 ( )
A.90 B.64
C.72 D.56
9.[2020·安庆期中] 将全体正奇数排成一个三角形数阵如图按照排列规律,第19行的第11个数是 .
10.[教材“思考”第3题变式] 某餐厅中1张桌子可坐6人,有如图示的两种摆放方式:
(1)对于方式一,4张桌子拼在一起可坐 人,对于方式二,n张桌子拼在一起可坐 人;
(2)该餐厅有30张这样的长方形桌子,由于受场地限制,可按方式一的拼法每5张拼成一张大桌子,或按方式二的拼法每6张拼成一张大桌子,一天中午,该餐厅来了98位顾客共同就餐,若你是这家餐厅的经理,你打算选择方式 来摆放桌子.
答案
1.D A项,2x+3y表示2x与3y的和,说法正确,不符合题意;
B项,表示5x除以2y所得的商,说法正确,不符合题意;
C项,9-y表示9减去y的所得的差,说法正确,不符合题意;
D项,a2+b2表示a的平方与b的平方的和,原来的说法错误,符合题意.故选D.
2.小金买了3个足球、2个篮球后剩余的钱数
3.(-1)n+1 分子依次为-1,1,3,5,7,9,…,相邻两个分子之间相差2,第n个数的分子可以表示为2n-3.
第一个数的分母为2=12+1,
第二个数的分母为5=22+1,
第三个数的分母为10=32+1,
…
所以第n个数的分母为n2+1,
所以第n个有理数是(-1)n+1(n为正整数).
故答案为(-1)n+1.
4.C 首先根据图示,可得第n个表格的左上角的数等于n,左下角的数等于n+1;右上角的数是左下角的数的2倍,右下角的数等于左下角的数与右上角的数的积加上左上角的数,所以a=20,b=10,x=20×10+9=209.
5.68 将图形分为两部分分析,第一行和最后一行都是一个星星,中间是一个方阵,根据第一个图形中间是3×3(个)星星,第二个图形中间是3×4(个)星星,依次类推即可得出答案.
观察图形的变化情况可知:
第1个图形中共有3×3+2=11(个)★;
第2个图形中共有3×4+2=14(个)★;
第3个图形中共有3×5+2=17(个)★;
…
第20个图形中共有3×22+2=68(个)★.
故答案为68.
6.3n+2 由图可得,
图①中棋子的个数为3×1+2=5,
图②中棋子的个数为3×2+2=8,
图③中棋子的个数为3×3+2=11,
……
则第n个“T”字形需要的棋子个数为3n+2.
7.B
8.A 观察图形,得出花盆个数变化的规律作答即可.第1个图形中,三角形每条边上有3个花盆, 共计(32-3)个花盆;第2个图形中,四边形每条边上有4个花盆, 共计(42-4)个花盆;第3个图形中, 五边形每条边上有5个花盆, 共计(52-5)个花盆……第n个图形中,(n+2)边形每条边上有(n+2)个花盆, 共计[(n+2)2-(n+2)]个花盆, 则第8个图形中花盆的个数为(8+2)2-(8+2)=90.故选A.
9.363 观察所给数阵,得每一行的变化规律如下:
第一行的第一个数为1×0+1=1,
第二行的第一个数为2×1+1=3,
第三行的第一个数为3×2+1=7,
…
第n行的第一个数为n(n-1)+1.
所以第19行的第一个数为19×18+1=343,
所以第19行的第11个数为343+10×2=363.
10.(1)18 (2n+4) (2)一
(1)对于方式一:4张桌子拼在一起可坐2+4×4=18(人),
对于方式二,n张桌子拼在一起可坐(2n+4)人.
故答案为18,(2n+4).
(2)按方式一,每5张桌子拼成一张大桌子,则一张大桌子可坐2+4×5=22(人),则30张桌子可拼成6张大桌子,共可坐22×6=132(人).
按方式二,每6张桌子拼成一张大桌子,则一张大桌子可坐2×6+4=16(人),则30张桌子可拼成5张大桌子,共可坐16×5=80(人).
因为132>98>80,所以应该按方式一的拼法摆放桌子.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
