初中数学苏科版九年级上册 第4章等可能条件下的概率 单元复习课 课件(共20张)
文档属性
| 名称 | 初中数学苏科版九年级上册 第4章等可能条件下的概率 单元复习课 课件(共20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 527.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
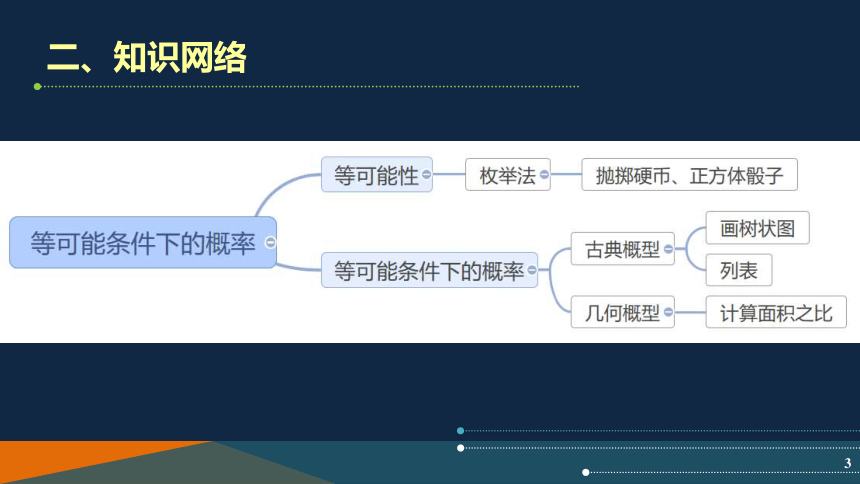
第4章等可能条件下的概率单元复习课苏科版义务教育教科书《数学》九年级上册一、学习目标1.在具体情境中了解事件发生的概率,能通过列表、画树状图等方法计算简单随机事件发生的概率.2.在概率的学习中培养和发展随机观念,初步形成用随机观念观察和分析问题的意识.二、知识网络三、知识清单等可能性1.一套书共有上、中、下三册,将它们任意摆放到书架的同一层上,按从左向右的顺序列出所有可能摆放的结果,这些结果的出现是等可能的吗?三、知识清单等可能性2.一只不透明的袋子中装有3个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到哪种颜色的球的可能性大?为什么?三、知识清单等可能条件下的概率——古典概型3.抛掷一枚质地均匀的骰子1次,朝上一面的点数是偶数的概率为.4.抛掷一枚质地均匀的骰子2次,点数之和为8的概率为.三、知识清单等可能条件下的概率——几何概型5.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率为.四、典型例题例1一只不透明的袋子中装有3个白球、1个红球,这些球除颜色外都相同,搅匀后从中任意摸出2个球(先摸出1个球,且这个球不放回,再摸出1个球)恰好是1个红球、1个白球的概率是多少 四、典型例题变式一只不透明的袋子中装有3个白球、1个红球,这些球除颜色外都相同,搅匀后从中任意摸出2个球(先摸出1个球,放回,搅匀后再摸出1个球)恰好是1个红球、1个白球的概率是多少 四、典型例题例2 4张相同的卡片上分别写有数字0、1、-2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)第一次抽取的卡片上数字是负数的概率为 ;(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)四、典型例题(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)四、典型例题变式 在一个不透明的布袋中装有三个小球,小球上分别标有数字-1、0、2,它们除了数字不同外,其他都完全相同.(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为 ;四、典型例题(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点 的纵坐标,请用树状图或表格列出点所有可能的坐标,并求出点落在如图所示的正方形网格内(包括边界)的概率.四、典型例题例3如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).四、典型例题(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).四、典型例题变式 如图,一块边长为30cm的正方形飞镖游戏板上画有半径分别为5cm、8cm、12cm的3个同心圆。假设飞镖投中游戏板上的每一点是等可能的(若投中圆的边界或没有投中游戏板,则重投1次),任意投掷飞镖1次,求下列事件发生的概率);(1)飞镖投中红色小圆;(2)飞镖投中黑色圆环.四、典型例题(1)飞镖投中红色小圆;四、典型例题(2)飞镖投中黑色圆环.五、课堂小结1.本节课我们复习了等可能条件下的概率,学会了通过画树状图或列表求事件的概率;2.在问题解决中培养和发展了随机观念,初步形成用随机观念观察和分析问题的意识.THE END
谢谢!
第4章等可能条件下的概率单元复习课苏科版义务教育教科书《数学》九年级上册一、学习目标1.在具体情境中了解事件发生的概率,能通过列表、画树状图等方法计算简单随机事件发生的概率.2.在概率的学习中培养和发展随机观念,初步形成用随机观念观察和分析问题的意识.二、知识网络三、知识清单等可能性1.一套书共有上、中、下三册,将它们任意摆放到书架的同一层上,按从左向右的顺序列出所有可能摆放的结果,这些结果的出现是等可能的吗?三、知识清单等可能性2.一只不透明的袋子中装有3个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到哪种颜色的球的可能性大?为什么?三、知识清单等可能条件下的概率——古典概型3.抛掷一枚质地均匀的骰子1次,朝上一面的点数是偶数的概率为.4.抛掷一枚质地均匀的骰子2次,点数之和为8的概率为.三、知识清单等可能条件下的概率——几何概型5.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率为.四、典型例题例1一只不透明的袋子中装有3个白球、1个红球,这些球除颜色外都相同,搅匀后从中任意摸出2个球(先摸出1个球,且这个球不放回,再摸出1个球)恰好是1个红球、1个白球的概率是多少 四、典型例题变式一只不透明的袋子中装有3个白球、1个红球,这些球除颜色外都相同,搅匀后从中任意摸出2个球(先摸出1个球,放回,搅匀后再摸出1个球)恰好是1个红球、1个白球的概率是多少 四、典型例题例2 4张相同的卡片上分别写有数字0、1、-2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)第一次抽取的卡片上数字是负数的概率为 ;(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)四、典型例题(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)四、典型例题变式 在一个不透明的布袋中装有三个小球,小球上分别标有数字-1、0、2,它们除了数字不同外,其他都完全相同.(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为 ;四、典型例题(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点 的纵坐标,请用树状图或表格列出点所有可能的坐标,并求出点落在如图所示的正方形网格内(包括边界)的概率.四、典型例题例3如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).四、典型例题(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).四、典型例题变式 如图,一块边长为30cm的正方形飞镖游戏板上画有半径分别为5cm、8cm、12cm的3个同心圆。假设飞镖投中游戏板上的每一点是等可能的(若投中圆的边界或没有投中游戏板,则重投1次),任意投掷飞镖1次,求下列事件发生的概率);(1)飞镖投中红色小圆;(2)飞镖投中黑色圆环.四、典型例题(1)飞镖投中红色小圆;四、典型例题(2)飞镖投中黑色圆环.五、课堂小结1.本节课我们复习了等可能条件下的概率,学会了通过画树状图或列表求事件的概率;2.在问题解决中培养和发展了随机观念,初步形成用随机观念观察和分析问题的意识.THE END
谢谢!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
