沪科版七年级上册1.4.1有理数的加法课件(共24张PPT)
文档属性
| 名称 | 沪科版七年级上册1.4.1有理数的加法课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 20:29:19 | ||
图片预览




文档简介
(共24张PPT)
第一章 有理数
1.4.1 有理数的加法
知识回顾
1.小学学过的加法类型是正数与正数相加、正数与0相加.
2.引入负数后,加法的类型还有哪几种呢?
例如:(+5)+(+3)= .
5 + 0 = .
8
5
负数与负数相加、
负数与正数相加、
负数与0相加.
情景导入
中国足球队在客场与卡塔尔的比赛中,上半场输了一个球,下半场经过艰苦奋战进了一个球,这场比赛中国队净胜球数是多少?
如果把赢一个球记作 +1
输一个球记作-1
则净胜球数为:
(-1) + (+1)= 0
获取新知
知识点1:有理数加法法则
探究: 一间0℃冷藏室连续两次改变温度:
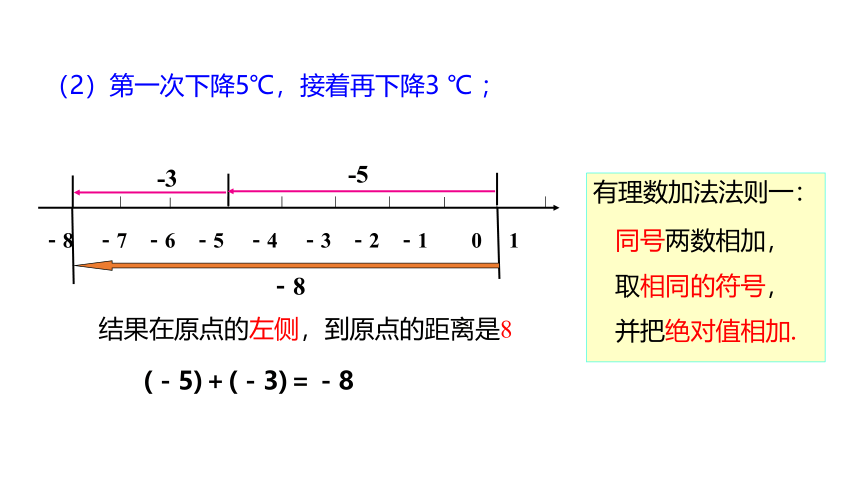
(2)第一次下降5℃,接着再下降3 ℃ ;
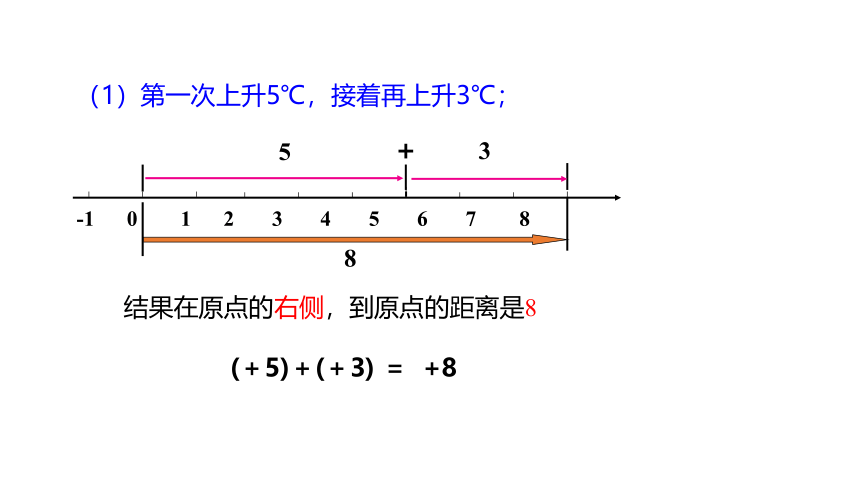
(1)第一次上升5℃,接着再上升3℃;
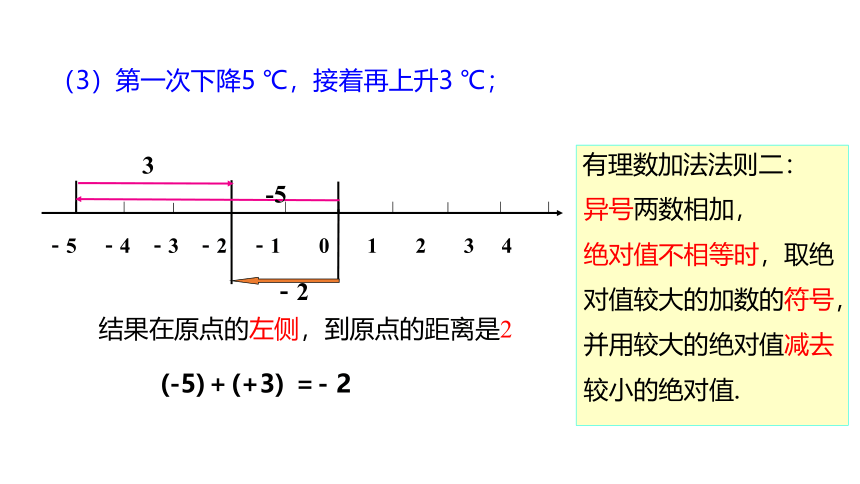
(3)第一次下降5 ℃ ,接着再上升3 ℃ ;
(4)第一次下降3 ℃ ,接着再上升5 ℃ ;
问:连续两次变化使温度共上升了多少摄氏度?
把温度上升记作正,温度下降记作负,在数轴上表示连续两次温度变化的总结果,并写出算式。
(+5)+(+3) = +8
-1 0 1 2 3 4 5 6 7 8
5
3
+
8
(1)第一次上升5℃,接着再上升3℃;
结果在原点的右侧,到原点的距离是8
有理数加法法则一:
(-5)+(-3)=-8
-8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
同号两数相加,
取相同的符号,
并把绝对值相加.
-5
-3
(2)第一次下降5℃,接着再下降3 ℃ ;
结果在原点的左侧,到原点的距离是8
(-5)+(+3) =- 2
-2
-5 -4 -3 -2 -1 0 1 2 3 4
-5
3
(3)第一次下降5 ℃,接着再上升3 ℃;
结果在原点的左侧,到原点的距离是2
有理数加法法则二:
异号两数相加,
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
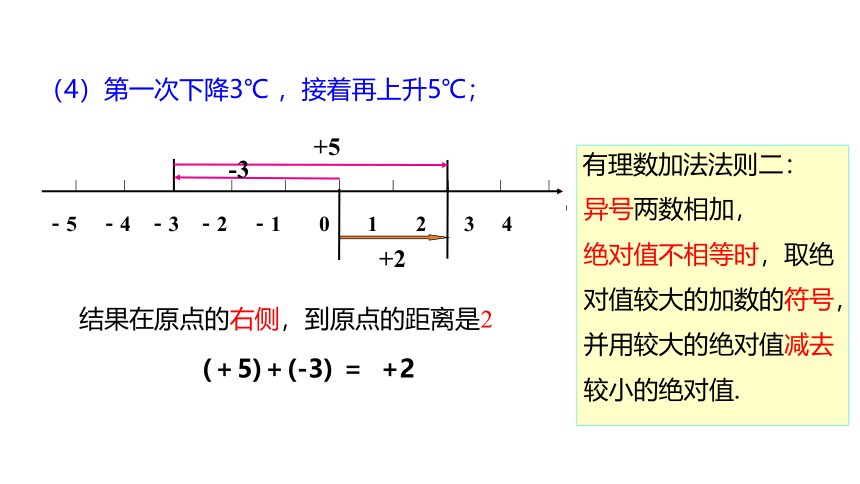
(+5)+(-3) = +2
结果在原点的右侧,到原点的距离是2
(4)第一次下降3℃ ,接着再上升5℃;
-5 -4 -3 -2 -1 0 1 2 3 4
-3
+5
+2
有理数加法法则二:
异号两数相加,
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
有理数加法法则二:
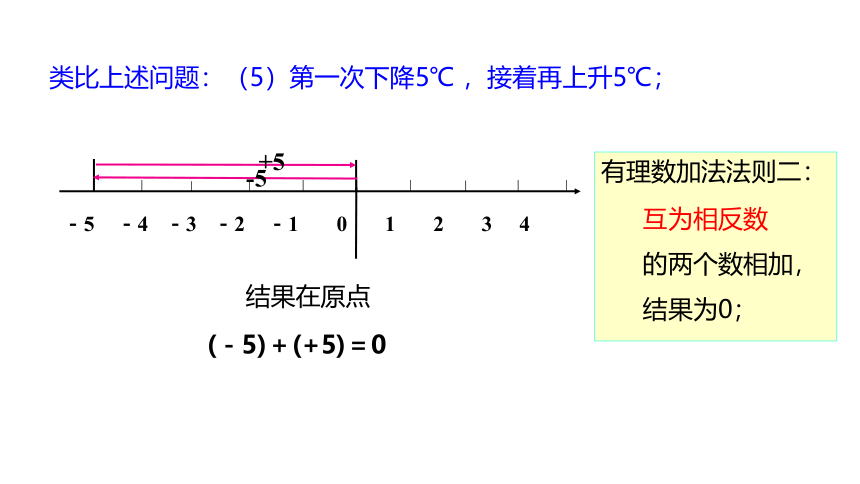
(-5)+(+5)=0
-5 -4 -3 -2 -1 0 1 2 3 4
-5
+5
互为相反数
的两个数相加,
结果为0;
类比上述问题:(5)第一次下降5℃ ,接着再上升5℃;
结果在原点
有理数加法法则三:
(-5)+0=-5
-5 -4 -3 -2 -1 0 1 2 3 4
-5
一个数与0相加,
仍得这个数.
类比上述问题:(5)第一次下降5℃ ,接着再上升0℃;
结果在原点的左侧,到原点的距离是5
有理数加法法则
(1)同号两数相加,取相同的符号,并把绝对值相加.
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,
并用较大的绝对值减较小的绝对值.
互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
备注:有条理的归纳加法法则,体会分类讨论思想 .
分析特征 强化理解 总结步骤
( -4 ) + ( - 8 ) = - ( 4 + 8 ) = - 12
↓ ↓ ↓ ↓
同号两数相加 取相同符号 两个加数的绝对值相加
( - 9 ) + ( + 2) = - ( 9 - 2) = -7
↓ ↓ ↓ ↓
异号两数相加 取绝对值 两个加数的绝对值
较大的符号 由大的减去小的
同号两数之和——这是名符其实的和,做加法.
异号两数之和——表面上叫“和”,其实是做减法.
例题讲解
例1 计算:
(2) (-5)+(-9);
(1) (+7)+(+6) ;
(4) (-10.5)+(+21.5) .
解:(1) (+7)+(+6)=+(7+6)=13
(2)(-5)+(-9)=-(5+9)=-14
(4) (-10.5)+(+21.5)
=+(21.5-10.5)
=11
有理数加法运算的基本步骤:
1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
同号相加一边倒,
异号相加“大”减“小”,
符号跟着大的跑,
绝对值相等零正好
(1)(-7.5)+(+7.5);
(2)(-3.5)+0.
解: (1)(-7.5)+(+7.5)=0
(2)(-3.5)+0=-3.5
例2 计算:
注意:互为相反数的两个数相加得0
例3 海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置.(上升为正,下潜为负)
解:潜水艇下潜40m,记作-40m;上升 15m,记作+15m.根据题意,得
(-40)+(+15)=-(40-25)=-25(m)
答:现在这艘潜艇位于海平面下25m处.
-50m
-30m
-20m
海平面
-10m
0m
-40m
知识点2:有理数加法的实际应用
例4 已知|a|=3,|b|=2,且a解:因为|a|=3,所以a=3或a=-3.
因为|b|=2,所以b=2或b=-2.
又因为a当a=-3,b=2时,a+b=(-3)+2=-1;
当a=-3,b=-2时,a+b=(-3)+(-2)=-5.
本题的解答体现了分类讨论思想,分类时要做到不重复不遗漏.
1.计算:(–3)+2=( )
A.5 B.–5 C.–1 D.+1
2.已知|a|=1,b是2的相反数,则a+b的值为( )
A.–3 B.–1 C.–1或–3 D.1或–3
C
C
随堂演练
3.两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
D
4.已知a+b<0,则对a,b的判断正确的是( )
A.a,b都为负
B.a,b一正一负,且负数的绝对值大于正数的绝对值
C.a,b其中一个为零,另一个为负数
D.以上三种都有可能
B
5. 对于两个有理数的和,下列说法正确的是( )
A.一定比任何一个有理数大
B.至少比其中一个有理数大
C.一定比任何一个有理数小
D.以上说法都不正确
D
6.计算下列各式:
(1)(-11)+(-9); (2)(-3.5)+(+7);
(3)(-1.08)+0; (4) .
解: (1)(-11)+(-9)=
(2)(-3.5)+(+7)=
(3)(-1.08)+0=-1.08;
(4) .
+
(7-3.5)=+3.5;
-
(11+9)=-20;
解:中午的气温为-25+11=-14(℃),
夜间的气温为-14+(-13)=-27(℃)
7.某城市一天早晨的气温是-25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
8.已知|a|=8,|b|=2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
解:(1)∵|a|=8,|b|=2,且a,b同号,
∴a=8,b=2;a=-8,b=-2,
则a+b=10或-10;
(2)∵|a|=8,|b|=2,且a,b异号,
∴a=8,b=-2;a=-8,b=2,
则a+b=6或-6.
课堂小结
有理数的加法
法则
基本步骤
2.再确定和的符号;
1.先判断类型(同号、异号等);
3.最后进行绝对值的加减运算.
应用
第一章 有理数
1.4.1 有理数的加法
知识回顾
1.小学学过的加法类型是正数与正数相加、正数与0相加.
2.引入负数后,加法的类型还有哪几种呢?
例如:(+5)+(+3)= .
5 + 0 = .
8
5
负数与负数相加、
负数与正数相加、
负数与0相加.
情景导入
中国足球队在客场与卡塔尔的比赛中,上半场输了一个球,下半场经过艰苦奋战进了一个球,这场比赛中国队净胜球数是多少?
如果把赢一个球记作 +1
输一个球记作-1
则净胜球数为:
(-1) + (+1)= 0
获取新知
知识点1:有理数加法法则
探究: 一间0℃冷藏室连续两次改变温度:
(2)第一次下降5℃,接着再下降3 ℃ ;
(1)第一次上升5℃,接着再上升3℃;
(3)第一次下降5 ℃ ,接着再上升3 ℃ ;
(4)第一次下降3 ℃ ,接着再上升5 ℃ ;
问:连续两次变化使温度共上升了多少摄氏度?
把温度上升记作正,温度下降记作负,在数轴上表示连续两次温度变化的总结果,并写出算式。
(+5)+(+3) = +8
-1 0 1 2 3 4 5 6 7 8
5
3
+
8
(1)第一次上升5℃,接着再上升3℃;
结果在原点的右侧,到原点的距离是8
有理数加法法则一:
(-5)+(-3)=-8
-8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
同号两数相加,
取相同的符号,
并把绝对值相加.
-5
-3
(2)第一次下降5℃,接着再下降3 ℃ ;
结果在原点的左侧,到原点的距离是8
(-5)+(+3) =- 2
-2
-5 -4 -3 -2 -1 0 1 2 3 4
-5
3
(3)第一次下降5 ℃,接着再上升3 ℃;
结果在原点的左侧,到原点的距离是2
有理数加法法则二:
异号两数相加,
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
(+5)+(-3) = +2
结果在原点的右侧,到原点的距离是2
(4)第一次下降3℃ ,接着再上升5℃;
-5 -4 -3 -2 -1 0 1 2 3 4
-3
+5
+2
有理数加法法则二:
异号两数相加,
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
有理数加法法则二:
(-5)+(+5)=0
-5 -4 -3 -2 -1 0 1 2 3 4
-5
+5
互为相反数
的两个数相加,
结果为0;
类比上述问题:(5)第一次下降5℃ ,接着再上升5℃;
结果在原点
有理数加法法则三:
(-5)+0=-5
-5 -4 -3 -2 -1 0 1 2 3 4
-5
一个数与0相加,
仍得这个数.
类比上述问题:(5)第一次下降5℃ ,接着再上升0℃;
结果在原点的左侧,到原点的距离是5
有理数加法法则
(1)同号两数相加,取相同的符号,并把绝对值相加.
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,
并用较大的绝对值减较小的绝对值.
互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
备注:有条理的归纳加法法则,体会分类讨论思想 .
分析特征 强化理解 总结步骤
( -4 ) + ( - 8 ) = - ( 4 + 8 ) = - 12
↓ ↓ ↓ ↓
同号两数相加 取相同符号 两个加数的绝对值相加
( - 9 ) + ( + 2) = - ( 9 - 2) = -7
↓ ↓ ↓ ↓
异号两数相加 取绝对值 两个加数的绝对值
较大的符号 由大的减去小的
同号两数之和——这是名符其实的和,做加法.
异号两数之和——表面上叫“和”,其实是做减法.
例题讲解
例1 计算:
(2) (-5)+(-9);
(1) (+7)+(+6) ;
(4) (-10.5)+(+21.5) .
解:(1) (+7)+(+6)=+(7+6)=13
(2)(-5)+(-9)=-(5+9)=-14
(4) (-10.5)+(+21.5)
=+(21.5-10.5)
=11
有理数加法运算的基本步骤:
1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
同号相加一边倒,
异号相加“大”减“小”,
符号跟着大的跑,
绝对值相等零正好
(1)(-7.5)+(+7.5);
(2)(-3.5)+0.
解: (1)(-7.5)+(+7.5)=0
(2)(-3.5)+0=-3.5
例2 计算:
注意:互为相反数的两个数相加得0
例3 海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置.(上升为正,下潜为负)
解:潜水艇下潜40m,记作-40m;上升 15m,记作+15m.根据题意,得
(-40)+(+15)=-(40-25)=-25(m)
答:现在这艘潜艇位于海平面下25m处.
-50m
-30m
-20m
海平面
-10m
0m
-40m
知识点2:有理数加法的实际应用
例4 已知|a|=3,|b|=2,且a
因为|b|=2,所以b=2或b=-2.
又因为a
当a=-3,b=-2时,a+b=(-3)+(-2)=-5.
本题的解答体现了分类讨论思想,分类时要做到不重复不遗漏.
1.计算:(–3)+2=( )
A.5 B.–5 C.–1 D.+1
2.已知|a|=1,b是2的相反数,则a+b的值为( )
A.–3 B.–1 C.–1或–3 D.1或–3
C
C
随堂演练
3.两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
D
4.已知a+b<0,则对a,b的判断正确的是( )
A.a,b都为负
B.a,b一正一负,且负数的绝对值大于正数的绝对值
C.a,b其中一个为零,另一个为负数
D.以上三种都有可能
B
5. 对于两个有理数的和,下列说法正确的是( )
A.一定比任何一个有理数大
B.至少比其中一个有理数大
C.一定比任何一个有理数小
D.以上说法都不正确
D
6.计算下列各式:
(1)(-11)+(-9); (2)(-3.5)+(+7);
(3)(-1.08)+0; (4) .
解: (1)(-11)+(-9)=
(2)(-3.5)+(+7)=
(3)(-1.08)+0=-1.08;
(4) .
+
(7-3.5)=+3.5;
-
(11+9)=-20;
解:中午的气温为-25+11=-14(℃),
夜间的气温为-14+(-13)=-27(℃)
7.某城市一天早晨的气温是-25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
8.已知|a|=8,|b|=2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
解:(1)∵|a|=8,|b|=2,且a,b同号,
∴a=8,b=2;a=-8,b=-2,
则a+b=10或-10;
(2)∵|a|=8,|b|=2,且a,b异号,
∴a=8,b=-2;a=-8,b=2,
则a+b=6或-6.
课堂小结
有理数的加法
法则
基本步骤
2.再确定和的符号;
1.先判断类型(同号、异号等);
3.最后进行绝对值的加减运算.
应用
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
