沪科版七年级上册2.1.1 用字母表示数(共19张PPT)
文档属性
| 名称 | 沪科版七年级上册2.1.1 用字母表示数(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 06:51:48 | ||
图片预览





文档简介
(共19张PPT)
第二章 整式的加减
2.1 .1 用字母表示数
a
b
c
知识回顾
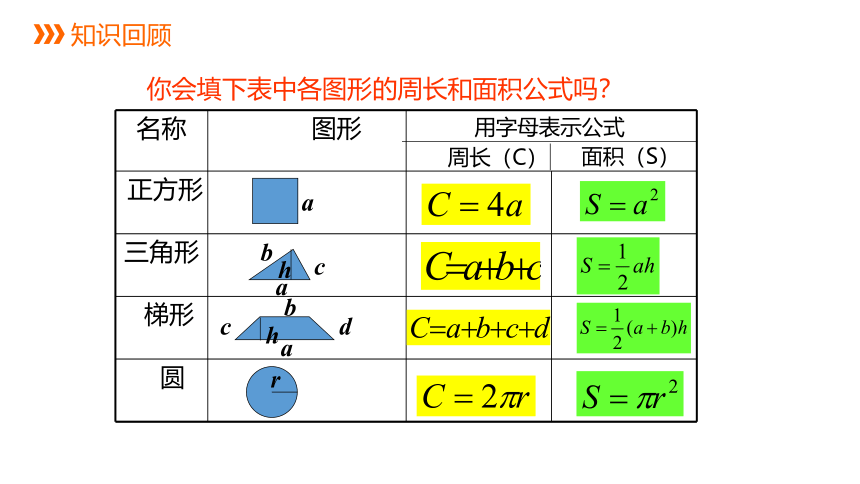
名称 图形 正方形
三角形
梯形
圆
用字母表示公式
周长(C)
面积(S)
a
h
a
b
h
r
c
d
你会填下表中各图形的周长和面积公式吗?
科学家爱因斯坦上小学时,在一次数学课中,发现
了下列的等式:
1+2=2+1,
3.5+5.6=5.6+3.5,
他认为,这是数的运算的一个重要规律,于是就把
这个规律告诉了他的老师和同学,得到了大家的赞赏.
情景导入
a+b=b+a
获取新知
问题1: 2008年9月25日我过成功发射了“神州七号”载人飞船,飞船在椭圆轨道上环绕地球飞过45周,历时68小时。
(1)该飞船绕地球飞行一周约需多分?
(2)若绕地球飞行n周,约需多少分?
(68×60)÷45=91(分)(精确到1分)
(68×60)÷45n=91n(分)(精确到1分)
问题2:能被2整除的整数叫做偶数,不能被2整除的整数叫做奇数,如果用k表示任意一个整数,用含有k的代数式表示:
任意一个偶数 .
任意一个奇数 .
2k ( 2k+2 或 2k-2 )
2k-1 ( 2k+1 )
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
31
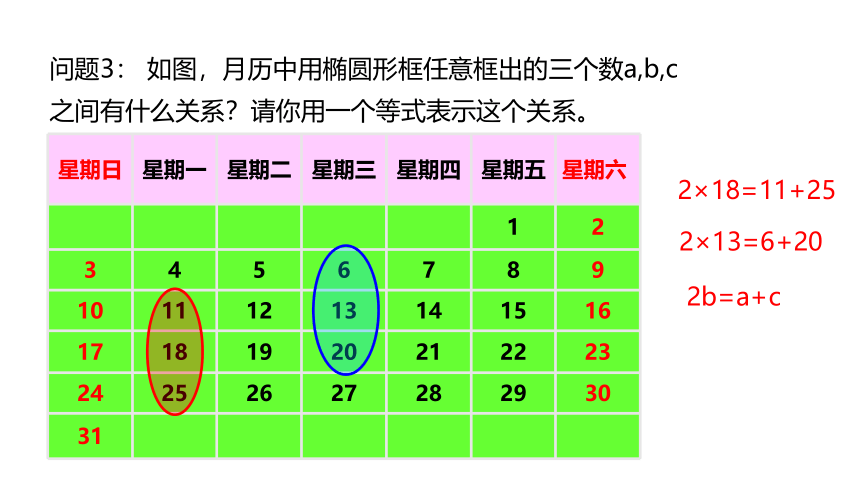
问题3: 如图,月历中用椭圆形框任意框出的三个数a,b,c之间有什么关系?请你用一个等式表示这个关系。
2×18=11+25
2×13=6+20
2b=a+c
a、b为任意有理数,则有:
加法交换律:a+b=b+a
加法结合律: (a+b)+c=a+(b+c)
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
问题4:用字母表示运算律
91n
2k ( 2k+2 或 2k-2 )
2k-1 ( 2k+1 )
2b=a+c
从上面是式子可以看出:用字母表示数,可以把一些数量关系更简明地表示出来,把具体的数换成抽象的字母,使所得的式子反映的规律具有普遍意义.
备注:
(1)同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示;
(2)用字母表示实际问题中的某个量时,字母取值必须使式子有意义且符合实际情况.
(1)全校学生总数是x,其中女生占总数52%,
则女生人数是 ,男生人数是 ;
(2)一个数比a的2倍小5,则这个数为 ;
(3)5箱苹果重m kg,每箱重 kg ;
(4)小红出生时爸爸28岁,小红a岁时,
爸爸 岁.
例1 填空:
数与字母相乘时,
数字通常写在字母的左边,乘号通常省略不写或写成“·”
遇到除法时,一般用分数的形式来写;
在实际问题中含有单位时,若式子含有和或差关系则用括号括起来
(a+28)
例题讲解
例2 填空:
(1)若m为整数,则2m为________数,2m-1为________数;
(2)三个连续偶数,若中间一个为2n,则其余两个为 ;
(3)若k为整数,以被4整除作为分类标准,则整数可分为
共4类;
(4)若一个两位数,其个位数字为a,十位数字为b,则这个两位数 为 .
2n-2,2n+2
10b+a
偶
奇
4k,4k+1,4k+2,4k+3
例3 用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子 枚(用含n的代数式表示).
方法一:除第一个图形有4枚棋子外,每多一个图形,多3枚棋子.
4+3(n-1)=3 n+1
第1个图
第2个图
第3个图
…
第1个图
第2个图
第3个图
…
方法二:每个图形,可看成是序列数与3的倍数又多1枚棋子:3n+1
第1个图
第2个图
第3个图
…
方法三: 2n+(n+1)=3n+1
1.购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为( )
A.(a+b)元 B.3(a+b)元
C.(3a+b)元 D.(a+3b)元
D
随堂演练
2.如图,是两同心圆,大圆半径为R,小圆半径为r,则阴影部分的面积为( )
A.πR2
B.πr2
C.πR2+πr2
D.πR2-πr2
D
A
3. “比a 的 倍大1的数”用式子表示为( )
4.填空:
(1)买单价为6元的钢笔a支,共需________元;
(2)一台电视机的标价为a元,则打八折后的售价为 ________ 元;
(3)温度由30 ℃下降t ℃后是________℃.
6a
0.8a
(30-t)
5. 如图,用火柴棒拼成一排由正方形组成的图形,如果图形中含有n个正方形,需要多少根火柴棒?
第一个正方形可以看成是1根火柴棒加3根火柴棒搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要 根
6.观察下列各式:
9-1=8,
16-4=12,25-9=16,36-16=20…
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n 的等式表示这个规律.
32-12=4×2,
42-22=4×3,
52-32=4×4,
62-42=4×5…
(n+2)2-n2=4(n+1),
解:
课堂小结
用字母表示数特点
一般性、限制性、普遍性
第二章 整式的加减
2.1 .1 用字母表示数
a
b
c
知识回顾
名称 图形 正方形
三角形
梯形
圆
用字母表示公式
周长(C)
面积(S)
a
h
a
b
h
r
c
d
你会填下表中各图形的周长和面积公式吗?
科学家爱因斯坦上小学时,在一次数学课中,发现
了下列的等式:
1+2=2+1,
3.5+5.6=5.6+3.5,
他认为,这是数的运算的一个重要规律,于是就把
这个规律告诉了他的老师和同学,得到了大家的赞赏.
情景导入
a+b=b+a
获取新知
问题1: 2008年9月25日我过成功发射了“神州七号”载人飞船,飞船在椭圆轨道上环绕地球飞过45周,历时68小时。
(1)该飞船绕地球飞行一周约需多分?
(2)若绕地球飞行n周,约需多少分?
(68×60)÷45=91(分)(精确到1分)
(68×60)÷45n=91n(分)(精确到1分)
问题2:能被2整除的整数叫做偶数,不能被2整除的整数叫做奇数,如果用k表示任意一个整数,用含有k的代数式表示:
任意一个偶数 .
任意一个奇数 .
2k ( 2k+2 或 2k-2 )
2k-1 ( 2k+1 )
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
31
问题3: 如图,月历中用椭圆形框任意框出的三个数a,b,c之间有什么关系?请你用一个等式表示这个关系。
2×18=11+25
2×13=6+20
2b=a+c
a、b为任意有理数,则有:
加法交换律:a+b=b+a
加法结合律: (a+b)+c=a+(b+c)
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
问题4:用字母表示运算律
91n
2k ( 2k+2 或 2k-2 )
2k-1 ( 2k+1 )
2b=a+c
从上面是式子可以看出:用字母表示数,可以把一些数量关系更简明地表示出来,把具体的数换成抽象的字母,使所得的式子反映的规律具有普遍意义.
备注:
(1)同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示;
(2)用字母表示实际问题中的某个量时,字母取值必须使式子有意义且符合实际情况.
(1)全校学生总数是x,其中女生占总数52%,
则女生人数是 ,男生人数是 ;
(2)一个数比a的2倍小5,则这个数为 ;
(3)5箱苹果重m kg,每箱重 kg ;
(4)小红出生时爸爸28岁,小红a岁时,
爸爸 岁.
例1 填空:
数与字母相乘时,
数字通常写在字母的左边,乘号通常省略不写或写成“·”
遇到除法时,一般用分数的形式来写;
在实际问题中含有单位时,若式子含有和或差关系则用括号括起来
(a+28)
例题讲解
例2 填空:
(1)若m为整数,则2m为________数,2m-1为________数;
(2)三个连续偶数,若中间一个为2n,则其余两个为 ;
(3)若k为整数,以被4整除作为分类标准,则整数可分为
共4类;
(4)若一个两位数,其个位数字为a,十位数字为b,则这个两位数 为 .
2n-2,2n+2
10b+a
偶
奇
4k,4k+1,4k+2,4k+3
例3 用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子 枚(用含n的代数式表示).
方法一:除第一个图形有4枚棋子外,每多一个图形,多3枚棋子.
4+3(n-1)=3 n+1
第1个图
第2个图
第3个图
…
第1个图
第2个图
第3个图
…
方法二:每个图形,可看成是序列数与3的倍数又多1枚棋子:3n+1
第1个图
第2个图
第3个图
…
方法三: 2n+(n+1)=3n+1
1.购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为( )
A.(a+b)元 B.3(a+b)元
C.(3a+b)元 D.(a+3b)元
D
随堂演练
2.如图,是两同心圆,大圆半径为R,小圆半径为r,则阴影部分的面积为( )
A.πR2
B.πr2
C.πR2+πr2
D.πR2-πr2
D
A
3. “比a 的 倍大1的数”用式子表示为( )
4.填空:
(1)买单价为6元的钢笔a支,共需________元;
(2)一台电视机的标价为a元,则打八折后的售价为 ________ 元;
(3)温度由30 ℃下降t ℃后是________℃.
6a
0.8a
(30-t)
5. 如图,用火柴棒拼成一排由正方形组成的图形,如果图形中含有n个正方形,需要多少根火柴棒?
第一个正方形可以看成是1根火柴棒加3根火柴棒搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要 根
6.观察下列各式:
9-1=8,
16-4=12,25-9=16,36-16=20…
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n 的等式表示这个规律.
32-12=4×2,
42-22=4×3,
52-32=4×4,
62-42=4×5…
(n+2)2-n2=4(n+1),
解:
课堂小结
用字母表示数特点
一般性、限制性、普遍性
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
