沪科版七年级上册1.5.3 有理数的乘、除混合运算(共25张PPT)
文档属性
| 名称 | 沪科版七年级上册1.5.3 有理数的乘、除混合运算(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 374.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 06:53:44 | ||
图片预览







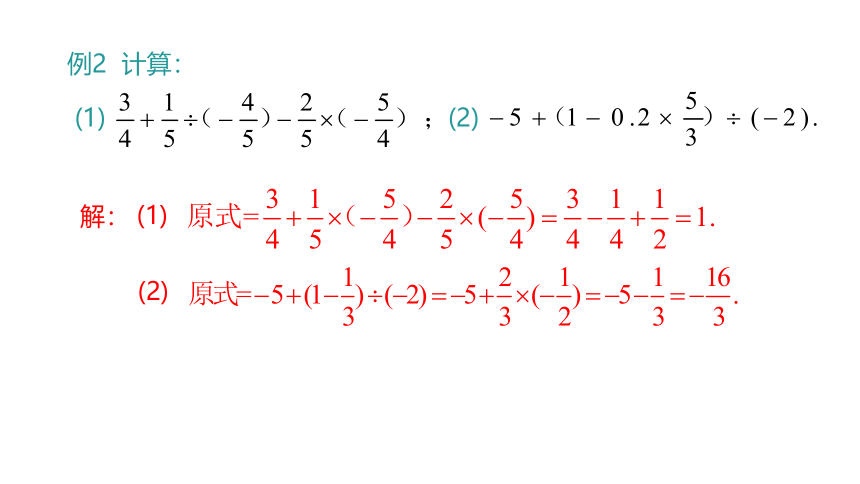
文档简介
(共25张PPT)
第一章 有理数
1.5.3 有理数的乘、除混合运算
知识回顾
1.有理数的乘法法则是什么?
4.小学时候大家学过乘法的哪些运算律?
乘法交换律、乘法结合律、乘法分配律
2.如何进行多个有理数的乘法运算?
(1)定号(奇负偶正) (2)算值(积的绝对值)
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0
3.有理数的除法法则是什么?
除以一个不为0的数,等于乘以这个数的倒数
数字入诗
明代南海才子伦文叙为苏东坡《百
鸟归巢图》题的数学诗:
天生一只又一只,三四五六七八只.
凤凰何少鸟何多,啄尽人间千石谷!
诗中数字:一只又一只,
三四五六七八只
请问何来百鸟呢
情景导入
在这些数中加上适当的运算符号就能得到100.
1+1+3×4+5×6+7×8=100
例题讲解
例1 计算:
(1)原式
(2)原式
解:
备注:有理数乘、除的混合运算,可统一化成乘法运算.
对于有理数的乘、除混合运算,应掌握以下几点:
(1)运算顺序:同级,从左至右依次运算,有括号就先算括号里的;
(2)将除法转化为乘法运算后,能约分的先约分;
(3)小数化为分数,带分数化为假分数.
获取新知
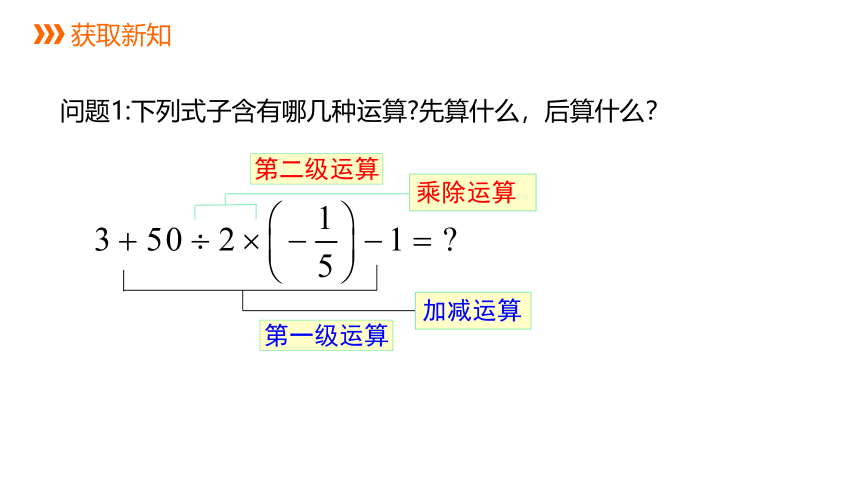
问题1:下列式子含有哪几种运算 先算什么,后算什么?
加减运算
第一级运算
乘除运算
第二级运算
问题2:观察式子 ,应该按照什么顺序来计算?
含加、减、乘、除的算式,如没有括号,应先做乘除运算,后做加减运算;如有括号,应先做括号里的运算。
有理数混合运算的顺序:
例2 计算:
(1) (2)
解:
(1)
(2)
获取新知
问题1: 计算下列各题,并比较它们的结果,你有什么发现?
请再举几个例子验证你的发现.
5× (-6) (-6) ×5
= -30
= -30
两个数相乘,交换因数的位置,积不变
乘法交换律:ab=ba
注意:用字母表示乘数时,“×”号可以写成“·”或省略, 如a×b可以写成a·b或ab.
5×(-6)= (-6)×5
问题2: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
[3×(-4)] × (-5) 3 ×[(-4) × (-5)]
= 60
= 60
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.
乘法结合律:(ab)c=a(bc)
[3×(-4)] × (-5) = 3 ×[(-4) × (-5)]
问题3: 计算下列各题,并比较它们的结果,
你有什么发现?请再举几个例子验证你的发现.
5 ×[3+(-7)] 5 ×3 + 5 ×(-7)
= -20
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律:a(b+c)=ab+ac
= -20
5 ×[3+(-7)]= 5 ×3 + 5 ×(-7)
归纳小结
1、乘法的交换律、结合律只涉及一种运算,而分配律要涉及两种运算.
2、分配律还可写成: ab+ac=a(b+c), 利用它有时也可以简化计算.
3、字母a、b、c可以表示正数、负数,也可以表示零,即a、b、c可以
表示任意有理数.
例3 计算:
解:
(分配律)
备注:利用分配律时,注意括号外的数字要和括号内的每一项都相乘
(2) (-0.1) ×(- 100) ×0.01 × (-10)
= -(0.1 × 100 ×0.01 ×10) (乘法符号法则)
=- [(0.1 × 10) ×(0.01 × 100)]
= -1.
(乘法交换律、结合律)
例4 计算
解:原式
乘法分配律的逆运算
随堂演练
B
1.在计算 ×(-36)时,可以避免通分的运算律是( )
A.加法交换律 B.乘法分配律
C.乘法交换律 D.加法结合律
2.计算 的结果是( )
A. B.
C. D.
B
C
3.下列变形不正确的是( )
A . 5×(-6)=(-6)×5
B. ×(-12)=(-12)×
C. ×(-4)=(-4)× + ×4
D.(-25)×(-16)×(-4)=[(-25)×(-4)]×(-16)
(2)
.
4.计算: (1) (2) .
解:(1)
;
5.计算:
解:(1)
(2)
6.学习有理数的乘法运算时,有这样一道计算题:
,比比看谁算的又快又准.
解:原式
原式
7.(中考 河北)请你参考黑板中老师(如图)的讲解,用运算律简便计算:
(1)999×(-15);
(2)999×118 +999× -999×18 .
解:(1)原式=(1 000-1)×(-15)
=-15 000+15
=-14 985.
课堂小结
有理数的乘除混合运算
乘法交换律:ab=ba
乘法结合律:(ab)c = a(bc) (三个以上也适用)
乘法分配律:a(b+c)=ab+ac(有时需要逆用)
乘除混合运算统一成乘法运算
乘除混合运算法则
运算律
第一章 有理数
1.5.3 有理数的乘、除混合运算
知识回顾
1.有理数的乘法法则是什么?
4.小学时候大家学过乘法的哪些运算律?
乘法交换律、乘法结合律、乘法分配律
2.如何进行多个有理数的乘法运算?
(1)定号(奇负偶正) (2)算值(积的绝对值)
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0
3.有理数的除法法则是什么?
除以一个不为0的数,等于乘以这个数的倒数
数字入诗
明代南海才子伦文叙为苏东坡《百
鸟归巢图》题的数学诗:
天生一只又一只,三四五六七八只.
凤凰何少鸟何多,啄尽人间千石谷!
诗中数字:一只又一只,
三四五六七八只
请问何来百鸟呢
情景导入
在这些数中加上适当的运算符号就能得到100.
1+1+3×4+5×6+7×8=100
例题讲解
例1 计算:
(1)原式
(2)原式
解:
备注:有理数乘、除的混合运算,可统一化成乘法运算.
对于有理数的乘、除混合运算,应掌握以下几点:
(1)运算顺序:同级,从左至右依次运算,有括号就先算括号里的;
(2)将除法转化为乘法运算后,能约分的先约分;
(3)小数化为分数,带分数化为假分数.
获取新知
问题1:下列式子含有哪几种运算 先算什么,后算什么?
加减运算
第一级运算
乘除运算
第二级运算
问题2:观察式子 ,应该按照什么顺序来计算?
含加、减、乘、除的算式,如没有括号,应先做乘除运算,后做加减运算;如有括号,应先做括号里的运算。
有理数混合运算的顺序:
例2 计算:
(1) (2)
解:
(1)
(2)
获取新知
问题1: 计算下列各题,并比较它们的结果,你有什么发现?
请再举几个例子验证你的发现.
5× (-6) (-6) ×5
= -30
= -30
两个数相乘,交换因数的位置,积不变
乘法交换律:ab=ba
注意:用字母表示乘数时,“×”号可以写成“·”或省略, 如a×b可以写成a·b或ab.
5×(-6)= (-6)×5
问题2: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
[3×(-4)] × (-5) 3 ×[(-4) × (-5)]
= 60
= 60
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.
乘法结合律:(ab)c=a(bc)
[3×(-4)] × (-5) = 3 ×[(-4) × (-5)]
问题3: 计算下列各题,并比较它们的结果,
你有什么发现?请再举几个例子验证你的发现.
5 ×[3+(-7)] 5 ×3 + 5 ×(-7)
= -20
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律:a(b+c)=ab+ac
= -20
5 ×[3+(-7)]= 5 ×3 + 5 ×(-7)
归纳小结
1、乘法的交换律、结合律只涉及一种运算,而分配律要涉及两种运算.
2、分配律还可写成: ab+ac=a(b+c), 利用它有时也可以简化计算.
3、字母a、b、c可以表示正数、负数,也可以表示零,即a、b、c可以
表示任意有理数.
例3 计算:
解:
(分配律)
备注:利用分配律时,注意括号外的数字要和括号内的每一项都相乘
(2) (-0.1) ×(- 100) ×0.01 × (-10)
= -(0.1 × 100 ×0.01 ×10) (乘法符号法则)
=- [(0.1 × 10) ×(0.01 × 100)]
= -1.
(乘法交换律、结合律)
例4 计算
解:原式
乘法分配律的逆运算
随堂演练
B
1.在计算 ×(-36)时,可以避免通分的运算律是( )
A.加法交换律 B.乘法分配律
C.乘法交换律 D.加法结合律
2.计算 的结果是( )
A. B.
C. D.
B
C
3.下列变形不正确的是( )
A . 5×(-6)=(-6)×5
B. ×(-12)=(-12)×
C. ×(-4)=(-4)× + ×4
D.(-25)×(-16)×(-4)=[(-25)×(-4)]×(-16)
(2)
.
4.计算: (1) (2) .
解:(1)
;
5.计算:
解:(1)
(2)
6.学习有理数的乘法运算时,有这样一道计算题:
,比比看谁算的又快又准.
解:原式
原式
7.(中考 河北)请你参考黑板中老师(如图)的讲解,用运算律简便计算:
(1)999×(-15);
(2)999×118 +999× -999×18 .
解:(1)原式=(1 000-1)×(-15)
=-15 000+15
=-14 985.
课堂小结
有理数的乘除混合运算
乘法交换律:ab=ba
乘法结合律:(ab)c = a(bc) (三个以上也适用)
乘法分配律:a(b+c)=ab+ac(有时需要逆用)
乘除混合运算统一成乘法运算
乘除混合运算法则
运算律
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
