沪科版数学七年级上册3.2 第1课时 等积变形与行程问题 同步课件(共26张PPT)
文档属性
| 名称 | 沪科版数学七年级上册3.2 第1课时 等积变形与行程问题 同步课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 08:30:21 | ||
图片预览








文档简介
(共26张PPT)
3.2 第1课时 等积变形与行程问题
第三章 一次方程与方程组
知识回顾
2.行程问题中常见的量都有什么?
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
情景导入
致100米的运动员:
一声枪响,
你们亮出自己的风采,
在这短短的100米中,
你们与时间争分夺秒,
只为了那最后的冲刺。
不管结果如何,你们都是胜利者。
因为,你们曾与时间竞赛。
在百米比赛中,裁判员会记录运动员所用的时间,你会计算运动员的速度吗?
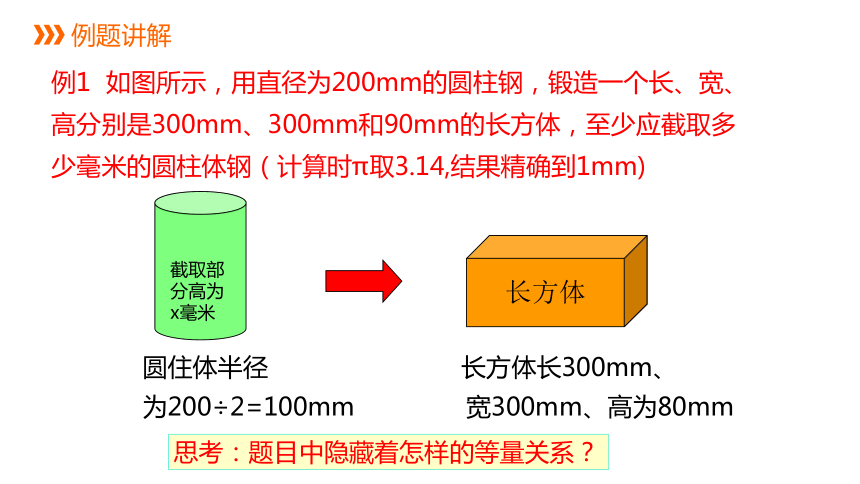
例1 如图所示,用直径为200mm的圆柱钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体,至少应截取多少毫米的圆柱体钢(计算时π取3.14,结果精确到1mm)
截取部分高为x毫米
长方体
圆住体半径 长方体长300mm、
为200÷2=100mm 宽300mm、高为80mm
思考:题目中隐藏着怎样的等量关系?
例题讲解
解:设应截取圆柱体钢长为 x mm.
根据题意得:
答:应截取约258mm长的圆柱体钢
3.14 ×( )2 x =300 ×300 ×90
解得 x≈258
分析:把圆柱体钢锻造成长方体毛坯,虽然形状发生了
变化,但锻造前后的体积是相等的,也就是
圆柱体体积=长方体体积.
圆柱体体积=πr2h
长方体体积=abc
例2 为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1 110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
分析:行程问题中常涉及的量有路程、平均速度、时间. 它们之间的基本关系是:
路程=平均速度×时间.
解:设提速前客车平均每时行驶x km,那么提速后客车平均每时行驶(x+40) km.客车行驶路程1 110 km,平均速度是(x+40) km/h,所需时间是10 h.根据题意,得
10(x+40)=1 110.
解方程,得 x=71.
答:提速前这趟客车的平均速度是71 km/h.
1、审:审题,分析题中各数量之间的关系
2、设:设未知数
3、找:找出能够表示题中全部含义的一个等量关系
4、列:根据等量关系列出方程
5、解:解方程,求出未知数的值
6、答: 检验所求的解,写出答案
通过例题的学习,你能总结列方程解应用题的一般步骤吗?
例3 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
线段图分析:
解:设 ,
则甲车行驶的路程为 米;
乙车行驶的路程为 千米。
根据相等关系
可列出方程 。
解得 。
答:B车行了3小时间后与A车相遇.
50x+30x=240
30x
50x
B车行了x 小时后与A车相遇
x=3
相遇问题:
甲路程+乙路程=总路程
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
线段图分析:
甲
乙
A
B
甲
乙
A
B
第一种情况:相遇前相距80千米
第二种情况:相遇后相距80千米
甲
乙
A
B
80千米
甲
乙
A
B
80千米
50x
30x
30x
50x
解:设两车行了x小时后相距80千米,
根据题意列方程得
相遇前:50x+30x+80=240
解得 x=2
相遇后:50x+30x - 80=240
解得 x=4
答:设两车行了2小时或4小时后相距80千米。
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
解决行程问题应注意:
(1)注意用线段图分析题意;
(2)注意行驶起点、行驶时间、行驶方向和行驶路径
(3)注意分类讨论
例4 兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设弟弟跑的时间为a分钟,
则哥哥跑的时间为 分钟.
弟弟跑的路程为 米,
哥哥跑的路程为 米.
弟弟跑的路程=哥哥跑的路程
200a=250(a-3)
【分析】
(a-3)
200a
250(a-3)
解:设弟弟跑的时间为a分钟,则哥哥跑的时间为(a-3)分钟.
根据题意列方程,得:
200a=250(a-3)
解得: a=15
所以:15×200=3000(米)
答:两人所跑的路程为3000米.
例5 甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
快
慢
甲站
乙站
450km
慢
快
65x
85x
【分析】
追击问题:快车路程-慢车路程=路程差
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
一般规律:在路程、速度、时间这三个量中,甲量已 知,从乙量设元,则从丙量中找相等关系列方程; 在所有行程问题中,一般都已知一个量,另两个量相互之间都存在关系.
速度(km/h) 时间(h) 路程(km)
顺水
逆水
例6 一船航行于A、B两个码头之间,顺水航行需要2小时,逆水航行需要2.5小时,已知水流速度是3km/h,求这两个码头之间的距离
A码头
B码头
水流方向
x+3
x - 3
2
2.5
2(x+3)
2.5( x- 3)
解:设船在静水中的速度是 x km/h
顺逆问题:
顺水速度=船速+水速
逆水速度=船速-水速
解:设船在静水中的速度是 x km/h,
根据题意得
2(x+3)=2.5(x-3)
解得x=27
2(x+3)=2×(27+3)=60
答:这两个码头之间的距离为60千米.
备注:顺逆问题是实际应用题的难点,主要是因为速度不是单一的量,是两个速度的和或者差.根据顺逆的路程相等列方程.
1.如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,其内部底面面积分别为80cm2,100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,乙中的水位高度比原先甲中的水位高度低了8cm,则甲容器的容积为( )
A. 1280cm3 B.2560cm3
C. 3200cm3 D. 4000cm3
随堂演练
C
D
2.从甲地到乙地,公共汽车原需行驶7小时,开通高速公路后,车速平均每小时增加了20千米,只需5个小时即可到达.则公共汽车提速后的速度是( )千米/时.
A. 40 B. 50 C. 60 D. 70
B
3.甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A.20千米/小时 B.60千米/小时
C.25千米/小时 D.75千米小时
单位不统一是行程问题最易出现的错误,注意统一单位
4.如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,设还需要x分钟才能到达B点,根据题意列方程为 .
5.要锻造直径为50cm,高为40cm 的圆柱毛坯, 需要截取边长
为20cm的方钢多长 设需要截取边长为20cm 的方钢 xcm, 根据题意得方程 .
6.一对学生去校外参加劳动,以4千米每时的速度步行前往,走了半小时,学校有紧急通知要传给队长,通讯员骑自行车以14千米每时的速度按原路追上去,通讯员要多少时间才能追上学生队伍?
解:设通讯员要x小时才能追上学生队伍,
根据题意得
4×0.5+4x=14x
解得 x=0.2
答:通讯员要0.2小时才能追上学生队伍
7.两运动员在田径场练习长跑,田径场周长是400米,已知甲每分钟跑200米,乙每分钟跑160米,两人同时 从同一地点出发,同向而行,经过 多少分钟两人才能第一次相遇?
解:设两个运动员第一次相遇所需要时间为x分钟。
根据题意得
200x-160x=400
解得 x=10
答:经过 10分钟两人才能第一次相遇.
8.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
课堂小结
行程问题
相遇问题:甲路程+乙路程=总路程
追击问题:快车路程-慢车路程=路程差
顺逆问题:
逆水速度=船速-水速
环形跑道问题:快的路程-慢的路程=1圈(第1次相遇)
顺水速度=船速+水速
变化前后的体积(或面积)不变
等积变形
3.2 第1课时 等积变形与行程问题
第三章 一次方程与方程组
知识回顾
2.行程问题中常见的量都有什么?
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
情景导入
致100米的运动员:
一声枪响,
你们亮出自己的风采,
在这短短的100米中,
你们与时间争分夺秒,
只为了那最后的冲刺。
不管结果如何,你们都是胜利者。
因为,你们曾与时间竞赛。
在百米比赛中,裁判员会记录运动员所用的时间,你会计算运动员的速度吗?
例1 如图所示,用直径为200mm的圆柱钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体,至少应截取多少毫米的圆柱体钢(计算时π取3.14,结果精确到1mm)
截取部分高为x毫米
长方体
圆住体半径 长方体长300mm、
为200÷2=100mm 宽300mm、高为80mm
思考:题目中隐藏着怎样的等量关系?
例题讲解
解:设应截取圆柱体钢长为 x mm.
根据题意得:
答:应截取约258mm长的圆柱体钢
3.14 ×( )2 x =300 ×300 ×90
解得 x≈258
分析:把圆柱体钢锻造成长方体毛坯,虽然形状发生了
变化,但锻造前后的体积是相等的,也就是
圆柱体体积=长方体体积.
圆柱体体积=πr2h
长方体体积=abc
例2 为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1 110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
分析:行程问题中常涉及的量有路程、平均速度、时间. 它们之间的基本关系是:
路程=平均速度×时间.
解:设提速前客车平均每时行驶x km,那么提速后客车平均每时行驶(x+40) km.客车行驶路程1 110 km,平均速度是(x+40) km/h,所需时间是10 h.根据题意,得
10(x+40)=1 110.
解方程,得 x=71.
答:提速前这趟客车的平均速度是71 km/h.
1、审:审题,分析题中各数量之间的关系
2、设:设未知数
3、找:找出能够表示题中全部含义的一个等量关系
4、列:根据等量关系列出方程
5、解:解方程,求出未知数的值
6、答: 检验所求的解,写出答案
通过例题的学习,你能总结列方程解应用题的一般步骤吗?
例3 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
线段图分析:
解:设 ,
则甲车行驶的路程为 米;
乙车行驶的路程为 千米。
根据相等关系
可列出方程 。
解得 。
答:B车行了3小时间后与A车相遇.
50x+30x=240
30x
50x
B车行了x 小时后与A车相遇
x=3
相遇问题:
甲路程+乙路程=总路程
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
线段图分析:
甲
乙
A
B
甲
乙
A
B
第一种情况:相遇前相距80千米
第二种情况:相遇后相距80千米
甲
乙
A
B
80千米
甲
乙
A
B
80千米
50x
30x
30x
50x
解:设两车行了x小时后相距80千米,
根据题意列方程得
相遇前:50x+30x+80=240
解得 x=2
相遇后:50x+30x - 80=240
解得 x=4
答:设两车行了2小时或4小时后相距80千米。
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
解决行程问题应注意:
(1)注意用线段图分析题意;
(2)注意行驶起点、行驶时间、行驶方向和行驶路径
(3)注意分类讨论
例4 兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设弟弟跑的时间为a分钟,
则哥哥跑的时间为 分钟.
弟弟跑的路程为 米,
哥哥跑的路程为 米.
弟弟跑的路程=哥哥跑的路程
200a=250(a-3)
【分析】
(a-3)
200a
250(a-3)
解:设弟弟跑的时间为a分钟,则哥哥跑的时间为(a-3)分钟.
根据题意列方程,得:
200a=250(a-3)
解得: a=15
所以:15×200=3000(米)
答:两人所跑的路程为3000米.
例5 甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
快
慢
甲站
乙站
450km
慢
快
65x
85x
【分析】
追击问题:快车路程-慢车路程=路程差
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
一般规律:在路程、速度、时间这三个量中,甲量已 知,从乙量设元,则从丙量中找相等关系列方程; 在所有行程问题中,一般都已知一个量,另两个量相互之间都存在关系.
速度(km/h) 时间(h) 路程(km)
顺水
逆水
例6 一船航行于A、B两个码头之间,顺水航行需要2小时,逆水航行需要2.5小时,已知水流速度是3km/h,求这两个码头之间的距离
A码头
B码头
水流方向
x+3
x - 3
2
2.5
2(x+3)
2.5( x- 3)
解:设船在静水中的速度是 x km/h
顺逆问题:
顺水速度=船速+水速
逆水速度=船速-水速
解:设船在静水中的速度是 x km/h,
根据题意得
2(x+3)=2.5(x-3)
解得x=27
2(x+3)=2×(27+3)=60
答:这两个码头之间的距离为60千米.
备注:顺逆问题是实际应用题的难点,主要是因为速度不是单一的量,是两个速度的和或者差.根据顺逆的路程相等列方程.
1.如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,其内部底面面积分别为80cm2,100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,乙中的水位高度比原先甲中的水位高度低了8cm,则甲容器的容积为( )
A. 1280cm3 B.2560cm3
C. 3200cm3 D. 4000cm3
随堂演练
C
D
2.从甲地到乙地,公共汽车原需行驶7小时,开通高速公路后,车速平均每小时增加了20千米,只需5个小时即可到达.则公共汽车提速后的速度是( )千米/时.
A. 40 B. 50 C. 60 D. 70
B
3.甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A.20千米/小时 B.60千米/小时
C.25千米/小时 D.75千米小时
单位不统一是行程问题最易出现的错误,注意统一单位
4.如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,设还需要x分钟才能到达B点,根据题意列方程为 .
5.要锻造直径为50cm,高为40cm 的圆柱毛坯, 需要截取边长
为20cm的方钢多长 设需要截取边长为20cm 的方钢 xcm, 根据题意得方程 .
6.一对学生去校外参加劳动,以4千米每时的速度步行前往,走了半小时,学校有紧急通知要传给队长,通讯员骑自行车以14千米每时的速度按原路追上去,通讯员要多少时间才能追上学生队伍?
解:设通讯员要x小时才能追上学生队伍,
根据题意得
4×0.5+4x=14x
解得 x=0.2
答:通讯员要0.2小时才能追上学生队伍
7.两运动员在田径场练习长跑,田径场周长是400米,已知甲每分钟跑200米,乙每分钟跑160米,两人同时 从同一地点出发,同向而行,经过 多少分钟两人才能第一次相遇?
解:设两个运动员第一次相遇所需要时间为x分钟。
根据题意得
200x-160x=400
解得 x=10
答:经过 10分钟两人才能第一次相遇.
8.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
课堂小结
行程问题
相遇问题:甲路程+乙路程=总路程
追击问题:快车路程-慢车路程=路程差
顺逆问题:
逆水速度=船速-水速
环形跑道问题:快的路程-慢的路程=1圈(第1次相遇)
顺水速度=船速+水速
变化前后的体积(或面积)不变
等积变形
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
