沪科版数学七年级上册3.3 第2课时 代入消元法 同步课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级上册3.3 第2课时 代入消元法 同步课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 08:31:15 | ||
图片预览





文档简介
(共22张PPT)
3.3 第2课时 代入消元法
第三章 一次方程与方程组
知识回顾
2.什么是二元一次方程组?
1.什么是二元一次方程?
含有两个未知数的一次方程,叫做二元一次方程.
由两个一次方程组成的含两个未知数的方程组就叫做二元一次方程组.
3.用含 x 的代数式表示 y .
①2x+9=y – 3 ②4x – 3y=72
y=2x+12
获取新知
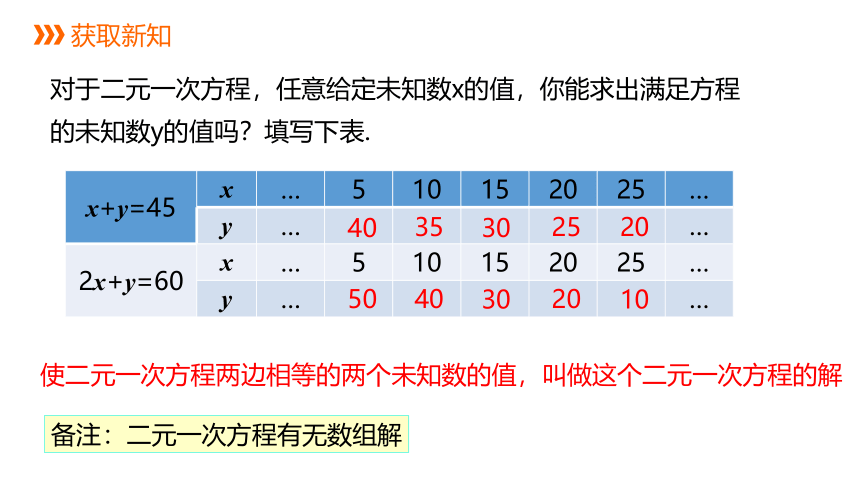
对于二元一次方程,任意给定未知数x的值,你能求出满足方程的未知数y的值吗?填写下表.
使二元一次方程两边相等的两个未知数的值,叫做这个二元一次方程的解
x+y=45 x … 5 10 15 20 25 …
y … …
2x+y=60 x … 5 10 15 20 25 …
y … …
备注:二元一次方程有无数组解
40
35
30
25
20
50
40
30
20
10
x+y=45 x … 5 10 15 20 25 …
y … 40 35 30 25 20 …
2x+y=60 x … 5 10 15 20 25 …
y … 50 40 30 20 10 …
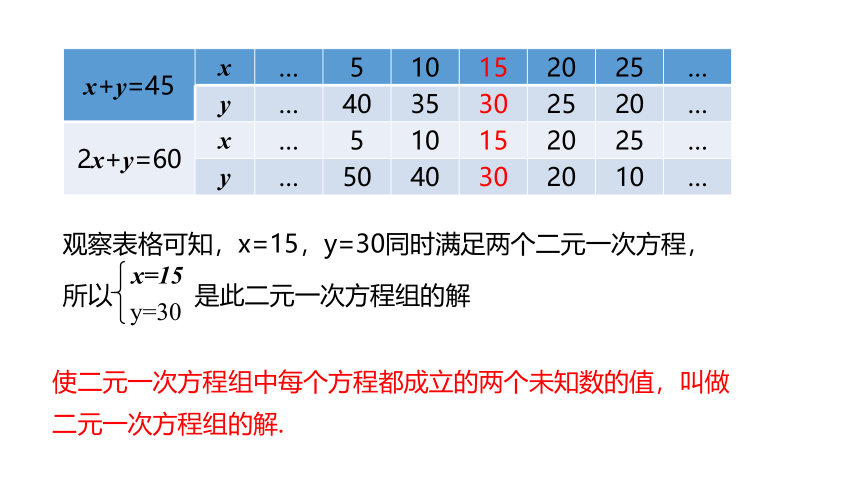
观察表格可知,x=15,y=30同时满足两个二元一次方程,
所以 是此二元一次方程组的解
x=15
y=30
使二元一次方程组中每个方程都成立的两个未知数的值,叫做二元一次方程组的解.
思考
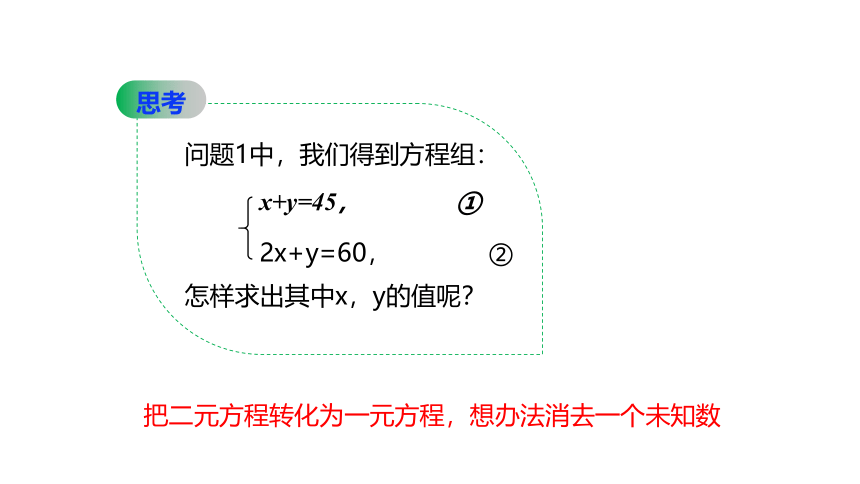
问题1中,我们得到方程组:
x+y=45, ①
2x+y=60, ②
怎样求出其中x,y的值呢?
把二元方程转化为一元方程,想办法消去一个未知数
解:由①得,
y=45 – x, ③
把③代入②,得
2x+(45 – x)=60,
解方程,得 x=15.
把x=15代入③,得 y=30.
所以,
x+y=45, ①
2x+y=60, ②
选择一个系数比较简单的方程,用含有x的代数式表示y(或用含有y的代数式表示x);
(1)变形:
将一个方程变形后代入另外一个方程中,消去一个未知数,得到一个一元一次方程;
(2)代入:
将得到的一元一次方程的解代入变形后的方程中,求得另一个未知数数的值;
(4)回代:
(3)解:
解得到的一元一次方程;
x=15
y=30
(5)写出答案:
x=a
y=b
解二元一次方程组的基本思想是“消元”,也就是要消去其中一个未知数,把解二元一次方程组转化成解一元一次方程.
从一个方程中求出某一个未知数的表达式,再把它“代入”另一个方程,进行求解,这种方法叫做代入消元法,简称代入法.
二元一次方程组
一元一次方程
消元
转化成
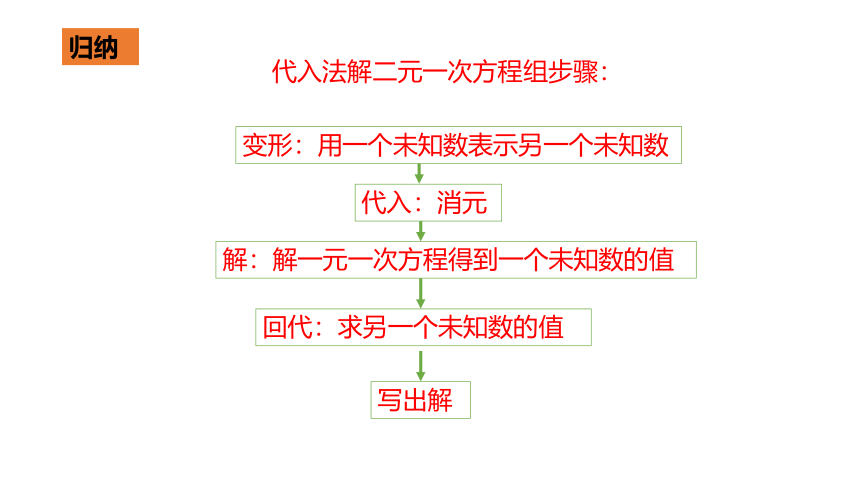
变形:用一个未知数表示另一个未知数
代入:消元
解:解一元一次方程得到一个未知数的值
回代:求另一个未知数的值
写出解
代入法解二元一次方程组步骤:
归纳
例1 解方程组:
2x+3y= – 7, ①
x+2y=3, ②
分析:要考虑将一个方程中的某个未知数用含另一个未知数的代数式表示.方程②中x的系数是1,因此,可以先将方程②变形,用含y的代数式表示x,再代入方程①求解.
例题讲解
解 : 由②,得 x=3 – 2y. ③
把③代入①,得
2(3 – 2y)+3y= –7.
-y=-13.
y=13.
把y=13代入③,得
x=3-2×13
x= – 23.
所以
x= – 23,
y=13.
m = 1 +2n
例2 若方程5x m-2n+4y 3n-m = 9是关于x、y的二元一次方程,求m 、n 的值.
由①,得
③
把③代入②,得
把n=2代入③,得
所以
n=2
m=5
解:
由题意知,
m - 2n = 1
3n – m = 1
①
②
3n –(1 + 2n)= 1
解方程,得
n = 2
m=5
即m 的值是5,n 的值是4.
y = 2 – 3x
由①,得
③
把③代入②,得
把x=2代入③,得
所以
x=2
y=-4
解:
由题意知,
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
解方程,得
x = 2
y=-4
即x 的值是2,y 的值是-4.
例3 如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
5x + 2(2 – 3x)- 2 = 0
分析:由二元一次方程解的定义知,方程的解一定能使方程左右两边的值相等.因此将 代入方程4x-3y=10中,即可得到一个关于m的一元一次方程.
例4 若 是方程4x-3y=10的一组解,求m的值.
解:由题意,得4(3m+1)-3(2m-2)=10.
解这个方程,得m=0.
随堂演练
1.二元一次方程组 的解为( )
x+2y=10
y=2x
x=4
y=3
A.
x=2
y=4
C.
x=3
y=6
B.
x=4
y=2
D.
C
2.二元一次方程3x+2y=17的正整数解的个数是( )
A.3个 B.2个 C.5个 D.4个
A
3.用代入法解方程组 下列说法正确的是( )
A.直接把①代入②,消去y
B.直接把①代入②,消去x
C.直接把②代入①,消去y
D.直接把②代入①,消去x
B
4.已知 是二元一次方程组 的解,则m-n的值是( )
A.1 B.2 C.3 D.4
D
5.用代入法解方程组 比较合理的变形是( )
A.由①得x=
B.由①得y=
C.由②得x=
D.由②得y=2x-5
D
解: 由①,得y=4-x.③
把③代入②,得2x-3(4-x)=3,
解这个方程,得x=3.
把x=3代入③,得y=1.
所以这个方程组的解是
6.解方程组:
7.对于某些数学问题,灵活运用整体思想,可以化难为易.在解二元一次方程组时,就可以运用整体代入法.如解方程组:
解:把②代入①,得x+2×1=3,解得x=1.
把x=1代入②,得y=0.
所以原方程组的解为
①
②
x=1,
y=0.
解:由①得2x-y=2,③
②可化为 2(2x-y)-y=9 ④
把③代入④,得2×2 - y=9,
解得y=- 5.
把y=-5代入③,得x=-1.5.
所以原方程组的解为
请用同样的方法解下面的方程组:
①
②
x=-1.5,
y=-5.
课堂小结
代入消元法
定义
步骤
变形:用一个未知数表示另一个未知数
代入:消元
解:解一元一次方程得到一个未知数的值
回代:求另一个未知数的值
写出解
整体代入法
3.3 第2课时 代入消元法
第三章 一次方程与方程组
知识回顾
2.什么是二元一次方程组?
1.什么是二元一次方程?
含有两个未知数的一次方程,叫做二元一次方程.
由两个一次方程组成的含两个未知数的方程组就叫做二元一次方程组.
3.用含 x 的代数式表示 y .
①2x+9=y – 3 ②4x – 3y=72
y=2x+12
获取新知
对于二元一次方程,任意给定未知数x的值,你能求出满足方程的未知数y的值吗?填写下表.
使二元一次方程两边相等的两个未知数的值,叫做这个二元一次方程的解
x+y=45 x … 5 10 15 20 25 …
y … …
2x+y=60 x … 5 10 15 20 25 …
y … …
备注:二元一次方程有无数组解
40
35
30
25
20
50
40
30
20
10
x+y=45 x … 5 10 15 20 25 …
y … 40 35 30 25 20 …
2x+y=60 x … 5 10 15 20 25 …
y … 50 40 30 20 10 …
观察表格可知,x=15,y=30同时满足两个二元一次方程,
所以 是此二元一次方程组的解
x=15
y=30
使二元一次方程组中每个方程都成立的两个未知数的值,叫做二元一次方程组的解.
思考
问题1中,我们得到方程组:
x+y=45, ①
2x+y=60, ②
怎样求出其中x,y的值呢?
把二元方程转化为一元方程,想办法消去一个未知数
解:由①得,
y=45 – x, ③
把③代入②,得
2x+(45 – x)=60,
解方程,得 x=15.
把x=15代入③,得 y=30.
所以,
x+y=45, ①
2x+y=60, ②
选择一个系数比较简单的方程,用含有x的代数式表示y(或用含有y的代数式表示x);
(1)变形:
将一个方程变形后代入另外一个方程中,消去一个未知数,得到一个一元一次方程;
(2)代入:
将得到的一元一次方程的解代入变形后的方程中,求得另一个未知数数的值;
(4)回代:
(3)解:
解得到的一元一次方程;
x=15
y=30
(5)写出答案:
x=a
y=b
解二元一次方程组的基本思想是“消元”,也就是要消去其中一个未知数,把解二元一次方程组转化成解一元一次方程.
从一个方程中求出某一个未知数的表达式,再把它“代入”另一个方程,进行求解,这种方法叫做代入消元法,简称代入法.
二元一次方程组
一元一次方程
消元
转化成
变形:用一个未知数表示另一个未知数
代入:消元
解:解一元一次方程得到一个未知数的值
回代:求另一个未知数的值
写出解
代入法解二元一次方程组步骤:
归纳
例1 解方程组:
2x+3y= – 7, ①
x+2y=3, ②
分析:要考虑将一个方程中的某个未知数用含另一个未知数的代数式表示.方程②中x的系数是1,因此,可以先将方程②变形,用含y的代数式表示x,再代入方程①求解.
例题讲解
解 : 由②,得 x=3 – 2y. ③
把③代入①,得
2(3 – 2y)+3y= –7.
-y=-13.
y=13.
把y=13代入③,得
x=3-2×13
x= – 23.
所以
x= – 23,
y=13.
m = 1 +2n
例2 若方程5x m-2n+4y 3n-m = 9是关于x、y的二元一次方程,求m 、n 的值.
由①,得
③
把③代入②,得
把n=2代入③,得
所以
n=2
m=5
解:
由题意知,
m - 2n = 1
3n – m = 1
①
②
3n –(1 + 2n)= 1
解方程,得
n = 2
m=5
即m 的值是5,n 的值是4.
y = 2 – 3x
由①,得
③
把③代入②,得
把x=2代入③,得
所以
x=2
y=-4
解:
由题意知,
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
解方程,得
x = 2
y=-4
即x 的值是2,y 的值是-4.
例3 如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
5x + 2(2 – 3x)- 2 = 0
分析:由二元一次方程解的定义知,方程的解一定能使方程左右两边的值相等.因此将 代入方程4x-3y=10中,即可得到一个关于m的一元一次方程.
例4 若 是方程4x-3y=10的一组解,求m的值.
解:由题意,得4(3m+1)-3(2m-2)=10.
解这个方程,得m=0.
随堂演练
1.二元一次方程组 的解为( )
x+2y=10
y=2x
x=4
y=3
A.
x=2
y=4
C.
x=3
y=6
B.
x=4
y=2
D.
C
2.二元一次方程3x+2y=17的正整数解的个数是( )
A.3个 B.2个 C.5个 D.4个
A
3.用代入法解方程组 下列说法正确的是( )
A.直接把①代入②,消去y
B.直接把①代入②,消去x
C.直接把②代入①,消去y
D.直接把②代入①,消去x
B
4.已知 是二元一次方程组 的解,则m-n的值是( )
A.1 B.2 C.3 D.4
D
5.用代入法解方程组 比较合理的变形是( )
A.由①得x=
B.由①得y=
C.由②得x=
D.由②得y=2x-5
D
解: 由①,得y=4-x.③
把③代入②,得2x-3(4-x)=3,
解这个方程,得x=3.
把x=3代入③,得y=1.
所以这个方程组的解是
6.解方程组:
7.对于某些数学问题,灵活运用整体思想,可以化难为易.在解二元一次方程组时,就可以运用整体代入法.如解方程组:
解:把②代入①,得x+2×1=3,解得x=1.
把x=1代入②,得y=0.
所以原方程组的解为
①
②
x=1,
y=0.
解:由①得2x-y=2,③
②可化为 2(2x-y)-y=9 ④
把③代入④,得2×2 - y=9,
解得y=- 5.
把y=-5代入③,得x=-1.5.
所以原方程组的解为
请用同样的方法解下面的方程组:
①
②
x=-1.5,
y=-5.
课堂小结
代入消元法
定义
步骤
变形:用一个未知数表示另一个未知数
代入:消元
解:解一元一次方程得到一个未知数的值
回代:求另一个未知数的值
写出解
整体代入法
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
