沪科版数学七年级上册3.4 第1课时 比赛与航行问题 同步课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级上册3.4 第1课时 比赛与航行问题 同步课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 234.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 08:32:15 | ||
图片预览







文档简介
(共22张PPT)
3.4 第1课时
比赛与航行问题
第三章 一次方程与方程组
列方程解应用题的一般步骤是什么?
审题
设元
列式
求解
写答
根据相等关系列出需要的代数式,并列出方程
弄清题意和题中的数量关系,即找出相等关系,可借助于示意图、表格等
用字母表示问题中的未知数
解这个方程,求出未知数的值
检查所得的值是否正确和符合实际情形,并写出答案
知识回顾
情境导入
隔壁听到人分银,
不知人数不知银.
每人五两多六两,
每人六两少五两.
多少人数多少银?
古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
例1 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分.试问该队胜几场,平几场?
审题:读题时抓住的关键信息
信息一:市第二中学足球队比赛11场,没有输过一场
说明胜场和平场共11场 .
信息二:胜一场得3分,平一场得1分,共得27分
说明胜场得分与平场得分共27分 .
胜场次+平场次=11
3×胜场次+1×平场次=27
例题讲解
解法一:一元一次方程
设该市第二中学足球队胜 x场,那么该队平(11-x)场.根据得分规定,胜x场,得3x分,平(11-x)场,得(11-x)分.共得分27分,得方程
解方程,得
答:该市第二中学足球队胜8场,平3场.
3x+(11-x)=27
x=8
11-x=11-8=3(场)
如果该市第二中学足球队胜的场数与平的场数分别用不同的未知数x,y来表 示,是否能列出方程组来求解呢
思考
又根据得分规定,胜x场,得3x分,平y场,得y分,共得27分,因而得方程 3x+y=27 ②
解方程①②组成的方程组,得
答:该市第二中学足球队胜8场,平3场.
解法二:二元一次方程组
设市第二中学足球队胜x场,平y场.由该队共比赛11场,
得方程 x+y=11 ①
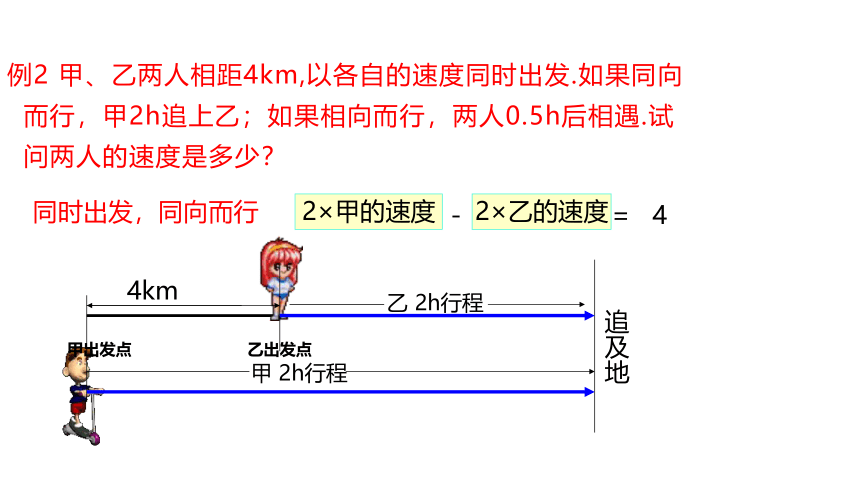
甲2h行程 - 乙2h行程 = 4
例2 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度是多少?
同时出发,同向而行
2×甲的速度
2×乙的速度
4km
追及地
甲 2h行程
甲出发点
乙出发点
乙 2h行程
乙出发点
4km
甲出发点
相遇地
甲0.5h行程
乙0.5h行程
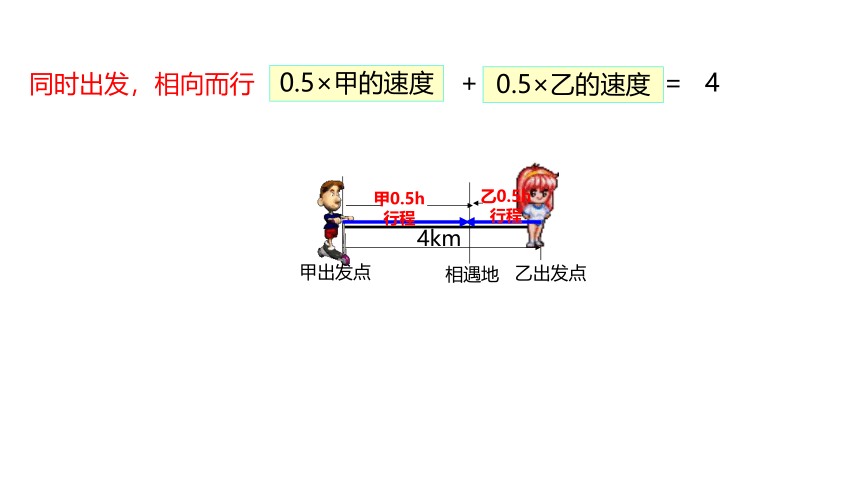
甲0.5h行程 + 乙0.5h行程 = 4
0.5×甲的速度
0.5×乙的速度
同时出发,相向而行
设元
解 设甲、乙的速度分别是 .
根据题意得,
②
①
列方程组
解方程组
②×4+①,得
答:甲的速度是5km/h,乙的速度是3km/h.
4x=20
x=5
将x=5代入①,得
y=3
所以
x=5
y=3
例3 我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9小时就能到达南京;返回时则用多了1小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
解:设火车的速度为xm/s,火车的长度为ym,
根据题意,得
解这个方程组,得
60x=1000+y
40x=1000-y
x=20
y=200
例4 某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
备注:从车头到车头或者从车尾到车尾之间的路程是火车行驶的路程.
答:火车的速度为20m/s,火车的长度为200m。
列二元一次方程组解应用题的一般步骤:
审
设
列
解
答
通过审题,把实际问题抽象成数学问题,分析已知数和未知数,找出能够表示题意两个相等关系
设两个未知数
根据这两个相等关系列出必需的代数式,从而列出方程组
解这个方程组,求出两个未知数的值
在对求出的方程组的解做出是否合理判断的基础上,写出答案
获取新知
行程问题中的等量关系
(1)基本关系:路程=速度x时间;
(2)相遇问题:两者的路程和=原来相距的路程;
(3)追及问题:两者的路程差=原来相距的路程;
(4)航行问题:
顺水(顺风)速度=静水(无风)速度十水速(风速);
逆水(逆风)速度=静水(无风)速度一水速(风速).
1.足球比赛的积分规则:胜一场得3分,平一场得1分,负一场得0分.一个队进行了14场比赛,其中负5场,共得19分,那么这个队胜的场数为( )
A.3场 B.4场 C.5场 D.6场
C
随堂练习
2.甲、乙两地相距360千米,一轮船往返于甲、乙两地之间,顺水行船用18小时,逆水行船用24小时,设轮船在静水中的速度为x千米/时,水流速度为y千米/时,则下列方程组中正确的是( )
A
3.甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,若设甲的速度为x米/秒,乙的速度为y米/秒,则下列方程组中正确的是( )
A
4.“珍爱生命,拒绝毒品”,学校举行的2017年禁毒知识竞赛共有60道题,曾浩同学答对了x道题,答错了y道题(不答视为答错),且答对题数比答错题数的7倍还多4道,那么下面列出的方程组中正确的是( )
A
5.一条船顺流航行是逆流航行的速度的3倍,这
条船在静水中的航速与水的流速之比为( )
A.3:1 B.2:1
C.4:1 D.5:2
B
6.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
解:设甲乙两车的速度分别为 x km/h、y km/h
根据题意,得
5y=6x
4y=4x+40
解得
x=50
y=6o
答:甲乙两车的速度分别为50km、60km
7.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.
解:设甲乙两人的速度分别为x m/min、y m/min
根据题意,得
2.5(x+y)=400
10(x-y )=400
解之得
x=100
y=60
答:甲乙两人的速度分别为100 m/min、60 m/min
课堂小结
实际问题
行程问题的
基本关系
步骤
行程问题中的等量关系
(1)基本关系:路程=速度x时间;
(2)相遇问题:两者的路程和=原来相距的路程;
(3)追及问题:两者的路程差=原来相距的路程;
(4)航行问题:
顺水(顺风)速度=静水(无风)速度十水速(风速);
逆水(逆风)速度=静水(无风)速度一水速(风速).
审、设、列、解、答
3.4 第1课时
比赛与航行问题
第三章 一次方程与方程组
列方程解应用题的一般步骤是什么?
审题
设元
列式
求解
写答
根据相等关系列出需要的代数式,并列出方程
弄清题意和题中的数量关系,即找出相等关系,可借助于示意图、表格等
用字母表示问题中的未知数
解这个方程,求出未知数的值
检查所得的值是否正确和符合实际情形,并写出答案
知识回顾
情境导入
隔壁听到人分银,
不知人数不知银.
每人五两多六两,
每人六两少五两.
多少人数多少银?
古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
例1 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分.试问该队胜几场,平几场?
审题:读题时抓住的关键信息
信息一:市第二中学足球队比赛11场,没有输过一场
说明胜场和平场共11场 .
信息二:胜一场得3分,平一场得1分,共得27分
说明胜场得分与平场得分共27分 .
胜场次+平场次=11
3×胜场次+1×平场次=27
例题讲解
解法一:一元一次方程
设该市第二中学足球队胜 x场,那么该队平(11-x)场.根据得分规定,胜x场,得3x分,平(11-x)场,得(11-x)分.共得分27分,得方程
解方程,得
答:该市第二中学足球队胜8场,平3场.
3x+(11-x)=27
x=8
11-x=11-8=3(场)
如果该市第二中学足球队胜的场数与平的场数分别用不同的未知数x,y来表 示,是否能列出方程组来求解呢
思考
又根据得分规定,胜x场,得3x分,平y场,得y分,共得27分,因而得方程 3x+y=27 ②
解方程①②组成的方程组,得
答:该市第二中学足球队胜8场,平3场.
解法二:二元一次方程组
设市第二中学足球队胜x场,平y场.由该队共比赛11场,
得方程 x+y=11 ①
甲2h行程 - 乙2h行程 = 4
例2 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度是多少?
同时出发,同向而行
2×甲的速度
2×乙的速度
4km
追及地
甲 2h行程
甲出发点
乙出发点
乙 2h行程
乙出发点
4km
甲出发点
相遇地
甲0.5h行程
乙0.5h行程
甲0.5h行程 + 乙0.5h行程 = 4
0.5×甲的速度
0.5×乙的速度
同时出发,相向而行
设元
解 设甲、乙的速度分别是 .
根据题意得,
②
①
列方程组
解方程组
②×4+①,得
答:甲的速度是5km/h,乙的速度是3km/h.
4x=20
x=5
将x=5代入①,得
y=3
所以
x=5
y=3
例3 我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9小时就能到达南京;返回时则用多了1小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
解:设火车的速度为xm/s,火车的长度为ym,
根据题意,得
解这个方程组,得
60x=1000+y
40x=1000-y
x=20
y=200
例4 某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
备注:从车头到车头或者从车尾到车尾之间的路程是火车行驶的路程.
答:火车的速度为20m/s,火车的长度为200m。
列二元一次方程组解应用题的一般步骤:
审
设
列
解
答
通过审题,把实际问题抽象成数学问题,分析已知数和未知数,找出能够表示题意两个相等关系
设两个未知数
根据这两个相等关系列出必需的代数式,从而列出方程组
解这个方程组,求出两个未知数的值
在对求出的方程组的解做出是否合理判断的基础上,写出答案
获取新知
行程问题中的等量关系
(1)基本关系:路程=速度x时间;
(2)相遇问题:两者的路程和=原来相距的路程;
(3)追及问题:两者的路程差=原来相距的路程;
(4)航行问题:
顺水(顺风)速度=静水(无风)速度十水速(风速);
逆水(逆风)速度=静水(无风)速度一水速(风速).
1.足球比赛的积分规则:胜一场得3分,平一场得1分,负一场得0分.一个队进行了14场比赛,其中负5场,共得19分,那么这个队胜的场数为( )
A.3场 B.4场 C.5场 D.6场
C
随堂练习
2.甲、乙两地相距360千米,一轮船往返于甲、乙两地之间,顺水行船用18小时,逆水行船用24小时,设轮船在静水中的速度为x千米/时,水流速度为y千米/时,则下列方程组中正确的是( )
A
3.甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,若设甲的速度为x米/秒,乙的速度为y米/秒,则下列方程组中正确的是( )
A
4.“珍爱生命,拒绝毒品”,学校举行的2017年禁毒知识竞赛共有60道题,曾浩同学答对了x道题,答错了y道题(不答视为答错),且答对题数比答错题数的7倍还多4道,那么下面列出的方程组中正确的是( )
A
5.一条船顺流航行是逆流航行的速度的3倍,这
条船在静水中的航速与水的流速之比为( )
A.3:1 B.2:1
C.4:1 D.5:2
B
6.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
解:设甲乙两车的速度分别为 x km/h、y km/h
根据题意,得
5y=6x
4y=4x+40
解得
x=50
y=6o
答:甲乙两车的速度分别为50km、60km
7.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.
解:设甲乙两人的速度分别为x m/min、y m/min
根据题意,得
2.5(x+y)=400
10(x-y )=400
解之得
x=100
y=60
答:甲乙两人的速度分别为100 m/min、60 m/min
课堂小结
实际问题
行程问题的
基本关系
步骤
行程问题中的等量关系
(1)基本关系:路程=速度x时间;
(2)相遇问题:两者的路程和=原来相距的路程;
(3)追及问题:两者的路程差=原来相距的路程;
(4)航行问题:
顺水(顺风)速度=静水(无风)速度十水速(风速);
逆水(逆风)速度=静水(无风)速度一水速(风速).
审、设、列、解、答
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
