沪科版数学七年级上册同步课件:3.4 第3课时 方案及其他问题(共19张PPT)
文档属性
| 名称 | 沪科版数学七年级上册同步课件:3.4 第3课时 方案及其他问题(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 191.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 17:26:38 | ||
图片预览





文档简介
(共19张PPT)
3.4 第3课时
方案及其他问题
第三章 一次方程与方程组
列方程解应用题的一般步骤是什么?
审题
设元
列式
求解
写答
根据相等关系列出需要的代数式,并列出方程
弄清题意和题中的数量关系,即找出相等关系,可借助于示意图、表格等
用字母表示问题中的未知数
解这个方程,求出未知数的值
检查所得的值是否正确和符合实际情形,并写出答案
知识回顾
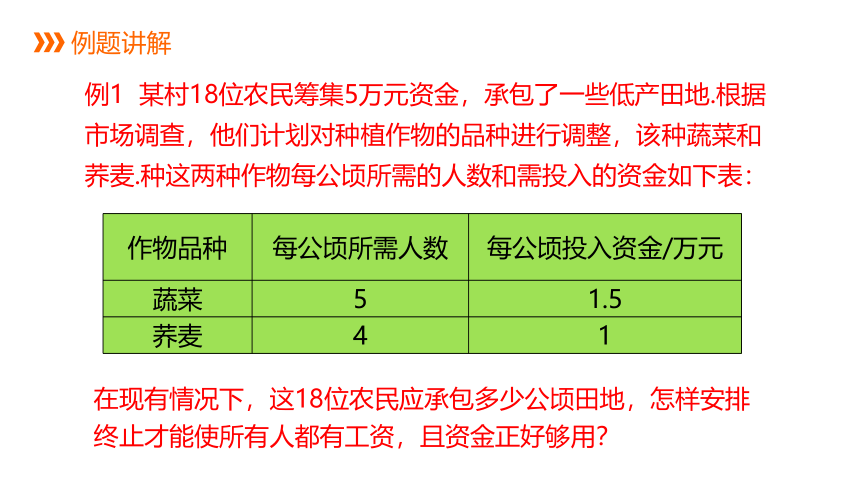
例1 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
例题讲解
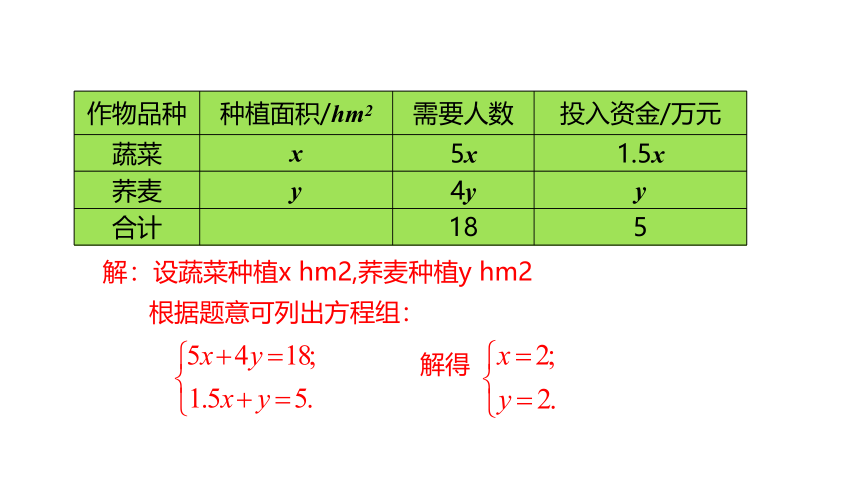
作物品种 种植面积/hm2 需要人数 投入资金/万元
蔬菜 x 5x 1.5x
荞麦 y 4y y
合计 18 5
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
解得
故,承包田地的面积为: x+y=4 (hm2)
人员安排为为:
5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
例2 动物园门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
每人门票价 14元 12元 10元
某校初一(1),(2)两个班共104人去植物园春游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算如果两班都以班为单位分别购票,则一共应付1344元.试问两个班各有多少名学生?他们如何购票比较合算?
解:设(1)班有x名学生,(2)班有y名学生,根据题意,得
x+y=104
14x+12y=1344
解方程组,得
x=48
y=56
若两个班集体购票,则需要花费
10×104=1040(元)
答:甲班有48名学生,乙班有56名学生,两个班集体购票比较合算.
例3 如图,8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位:cm)
x+y=60
x=3y
解:设小长方形地砖的长为xcm, 宽为ycm,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
60
备注:充分观察图形找到隐含的数量关系
例4 小丽4年前的年龄与小华4年后的年龄相等,3年后她们俩人的年龄和等于她们俩人年龄差的3倍. 求小华和小丽今年的年龄.
解:设小华今年为x岁,小丽今年y岁,根据题意得
解这个方程组得
答:小华今年5岁,小丽今年13岁.
1.为奖励消防演练活动中表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,在购买资金恰好用尽的情况下,购买方案有( )
A.4种 B.3种 C.2种 D.1种
B
随堂练习
2.植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
D
3.如图,7个一样大小的小长方形恰好拼成一个大长方形,若大长方形的宽为7 cm,则每一个小长方形的面积为 ( )
A. 7 cm2 B. 20 cm2
C. 14 cm2 D. 10 cm2
D
4.现在哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就18岁了.”如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,那么下列方程组正确的是( )
D
5.一个两位数的十位数字与个位数字的和是9,把这个两位数加上27,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,下面所列方程组正确的是( )
B
6.为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.这两种消毒液的单价各是多少元?
解:设 种消毒液的单价是x 元, 型消毒液的单价是y 元.
由题意得: ,
解得, ,
答: 种消毒液的单价是7元, 型消毒液的单价是9元.
7.某运输公司有A、B两种货车,3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨.
(1)请问1辆A货车和1辆B货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货车均满载),其中每辆A货车一次运货花费500元,每辆B货车一次运货花费400元.请你列出所有的运输方案,并指出哪种运输方案费用最少.
解:(1)1辆A货车和1辆B货车一次可以分别运货x吨和y吨,
根据题意可得: ,
解得: ,
答:1辆A货车和1辆B货车一次可以分别运货20吨和15吨;
3x+2y =90,
5x+4y=160.
x =20,
y=15.
(2)设安排A型车m辆,B型车n辆,
依题意得:20m+15n=190,即 ,
又∵m,n均为正整数,
∴ 或 或 ,
∴共有3种运输方案,
方案1:安排A型车8辆,B型车2辆;所需费用:500 8+400 2=4800(元);
方案2:安排A型车5辆,B型车6辆;所需费用:500 5+400 6=4900(元);
方案3:安排A型车2辆,B型车10辆.所需费用:500 2+400 10=5000(元);
∵4800<4900<5000,
∴安排A型车8辆,B型车2辆最省钱,最省钱的运输费用为4800元.
m=8,
n=2.
m=5,
n=6.
m=2,
n=10.
课堂小结
实际问题
方案问题
其他问题
年龄问题
数字问题
图形面积
3.4 第3课时
方案及其他问题
第三章 一次方程与方程组
列方程解应用题的一般步骤是什么?
审题
设元
列式
求解
写答
根据相等关系列出需要的代数式,并列出方程
弄清题意和题中的数量关系,即找出相等关系,可借助于示意图、表格等
用字母表示问题中的未知数
解这个方程,求出未知数的值
检查所得的值是否正确和符合实际情形,并写出答案
知识回顾
例1 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
例题讲解
作物品种 种植面积/hm2 需要人数 投入资金/万元
蔬菜 x 5x 1.5x
荞麦 y 4y y
合计 18 5
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
解得
故,承包田地的面积为: x+y=4 (hm2)
人员安排为为:
5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
例2 动物园门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
每人门票价 14元 12元 10元
某校初一(1),(2)两个班共104人去植物园春游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算如果两班都以班为单位分别购票,则一共应付1344元.试问两个班各有多少名学生?他们如何购票比较合算?
解:设(1)班有x名学生,(2)班有y名学生,根据题意,得
x+y=104
14x+12y=1344
解方程组,得
x=48
y=56
若两个班集体购票,则需要花费
10×104=1040(元)
答:甲班有48名学生,乙班有56名学生,两个班集体购票比较合算.
例3 如图,8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位:cm)
x+y=60
x=3y
解:设小长方形地砖的长为xcm, 宽为ycm,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
60
备注:充分观察图形找到隐含的数量关系
例4 小丽4年前的年龄与小华4年后的年龄相等,3年后她们俩人的年龄和等于她们俩人年龄差的3倍. 求小华和小丽今年的年龄.
解:设小华今年为x岁,小丽今年y岁,根据题意得
解这个方程组得
答:小华今年5岁,小丽今年13岁.
1.为奖励消防演练活动中表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,在购买资金恰好用尽的情况下,购买方案有( )
A.4种 B.3种 C.2种 D.1种
B
随堂练习
2.植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
D
3.如图,7个一样大小的小长方形恰好拼成一个大长方形,若大长方形的宽为7 cm,则每一个小长方形的面积为 ( )
A. 7 cm2 B. 20 cm2
C. 14 cm2 D. 10 cm2
D
4.现在哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就18岁了.”如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,那么下列方程组正确的是( )
D
5.一个两位数的十位数字与个位数字的和是9,把这个两位数加上27,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,下面所列方程组正确的是( )
B
6.为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.这两种消毒液的单价各是多少元?
解:设 种消毒液的单价是x 元, 型消毒液的单价是y 元.
由题意得: ,
解得, ,
答: 种消毒液的单价是7元, 型消毒液的单价是9元.
7.某运输公司有A、B两种货车,3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨.
(1)请问1辆A货车和1辆B货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货车均满载),其中每辆A货车一次运货花费500元,每辆B货车一次运货花费400元.请你列出所有的运输方案,并指出哪种运输方案费用最少.
解:(1)1辆A货车和1辆B货车一次可以分别运货x吨和y吨,
根据题意可得: ,
解得: ,
答:1辆A货车和1辆B货车一次可以分别运货20吨和15吨;
3x+2y =90,
5x+4y=160.
x =20,
y=15.
(2)设安排A型车m辆,B型车n辆,
依题意得:20m+15n=190,即 ,
又∵m,n均为正整数,
∴ 或 或 ,
∴共有3种运输方案,
方案1:安排A型车8辆,B型车2辆;所需费用:500 8+400 2=4800(元);
方案2:安排A型车5辆,B型车6辆;所需费用:500 5+400 6=4900(元);
方案3:安排A型车2辆,B型车10辆.所需费用:500 2+400 10=5000(元);
∵4800<4900<5000,
∴安排A型车8辆,B型车2辆最省钱,最省钱的运输费用为4800元.
m=8,
n=2.
m=5,
n=6.
m=2,
n=10.
课堂小结
实际问题
方案问题
其他问题
年龄问题
数字问题
图形面积
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
