沪科版数学七年级上册4.3 线段的长短比较 同步课件(共29张PPT)
文档属性
| 名称 | 沪科版数学七年级上册4.3 线段的长短比较 同步课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 417.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
4.3 线段的长短比较
第四章 直线与角
知识回顾
1.基本事实:
经过两点有一条直线,且只有一条直线.
(两点确定一条直线)
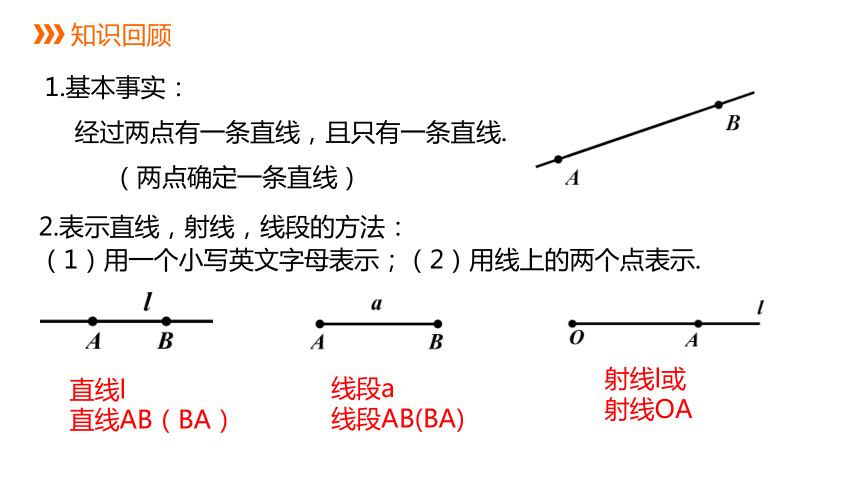
2.表示直线,射线,线段的方法:
(1)用一个小写英文字母表示;(2)用线上的两个点表示.
线段a
线段AB(BA)
射线l或
射线OA
直线l
直线AB(BA)
情景导入
小明
小华
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
小明
小华
思考:你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
②让两个同学站在同一平地上,脚底平齐,观看
两人的头顶,直接比出高矮.
——叠合法.
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
获取新知
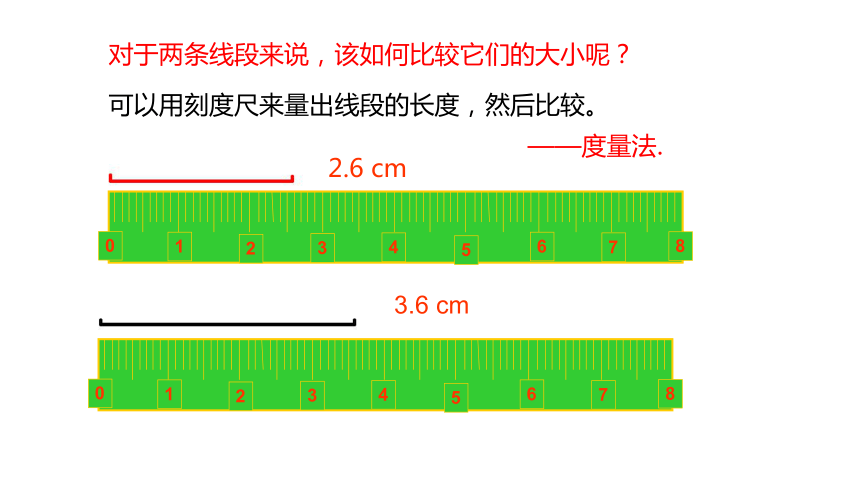
对于两条线段来说,该如何比较它们的大小呢?
可以用刻度尺来量出线段的长度,然后比较。
——度量法.
2.6 cm
1
2
3
5
4
6
7
8
0
3.6 cm
1
2
3
5
4
6
7
8
0
叠合法结论:
C
D
(A)
B
C
D
A
B
B
(A)
B
A
B
A
C
D
(A)
(B)
3. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.
<
1. 若点 A 与点 C 重合,点 B 与点 D ,那么 AB = CD.
重合
>
2. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB CD.
比较线段长短的两种方法
1、度量法——从“数值”的角度比较
2、叠合法—— 从“形”的角度比较
起点对齐,看终点
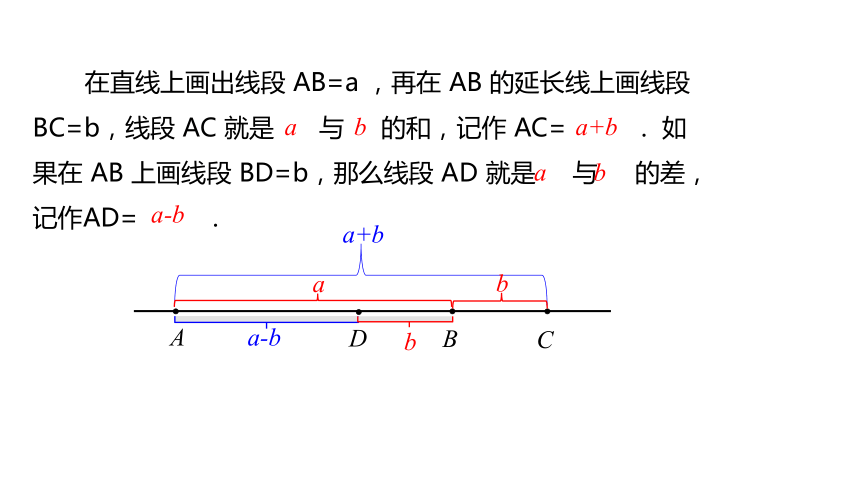
在直线上画出线段 AB=a ,再在 AB 的延长线上画线段
BC=b,线段 AC 就是 与 的和,记作 AC= . 如
果在 AB 上画线段 BD=b,那么线段 AD 就是 与 的差,
记作AD= .
a
b
a+b
a-b
a
b
A
B
C
D
a+b
a-b
a
b
b
A
B
M
思考:将一条绳子对折,使绳子的端点重合,说说你的感受.你能找到线段的中点吗?三等分点?四等分点?
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.类似的,还有线段的三等分点、四等分点等.
线段的三等分点
线段的四等分点
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
点 M , N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
备注:求线段的长度时,当题目中涉及到线段长度的比例或倍分关系时,通常可以设未知数,运用方程思想求解.
对线段的中点的认识:
(1)线段的中点是线段上的点,且把线段分成相等
的两条线段;
(2)一条线段的中点有且只有一个;
(3)如图,若M是AB的中点,则①AM=BM= AB;
②AB=2AM=2BM;③AM+BM=AB且AM=BM.反过来也成立.
思考:如图是连结A、B两点之间各种形状的线绳,如果将它们都展直,你能从中得到什么启发?
A·
·B
基本事实:两点之间的所有连线中,线段最短.
把原来弯曲的河道改直,A,B 两地间的河道长度有什么变化?
A,B 两地间的河道长度变短.
基本事实:两点之间的所有连线中,线段最短.
(即两点之间,线段最短)
两点之间线段的长度,叫做这两点之间的距离.
备注:距离不是线段.
线段是一个几何图形;
距离是一个量,它反映的是线段的长短.距离是一个数量且有长度单位.
A
B
例题讲解
例1 已知:线段AB =4,延长AB至点C,使AC = 11.点 D是AB的中点,点E是AC的中点.求DE的长.
如图,因为AB=4,点D为AB中点,故 AD = 2.
又因为AC = 11,点E为AC中点,AE=5.5.
故 DE= AE - AD = 5. 5 - 2 = 3. 5.
解:
例2 C为线段AB上一点,D是线段AC的中点,E为线段CB的中点,
AB=9cm,AC=5cm.
求:(1)AD的长;
(2)求DE的长.
解:(1)因为D是AC的中点,AC=5cm,
所以AD= AC=2.5cm.
(2)因为 CB=AB-AC=9-5=4cm,E是BC的中点,
所以CE= CB=2cm.
所以 DE=DC+CE=2.5+2=4.5cm
例3 直线a表示一条河,在河两侧有两个村庄A和B。要在河边建一个供水站C,使C到两村庄的距离之和最小。请找出C点的位置,并说明理由。
a
A
B
C
点C即为所求. 理由:两点之间,线段最短
在解决选择位置、求最短距离等问题时,通常利用“两点之间,线段最短”.
例4 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
解析:分以下两种情况进行讨论:
当点C在AB之间上,故AC=AB-BC=1cm;
当点C在AB的延长线上时,AC=AB+BC=9cm.
C
1.为了比较线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,结果点B在线段CD的延长线上,则( )
A.ABCD
C.AB=CD D.以上都不对
B
随堂演练
B
2 .如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
3. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
C
4.下列说法正确的是( )
A.若AC= AB,则C是AB的中点
B.若AB=2CB,则C是AB的中点
C.若AC=BC,则C是AB的中点
D.若AC=BC= AB,则C是AB的中点
D
C
5. 如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )
A. AC = CB B. AB = 2 AC
C. AC + CB = AB D. CB = AB
A
C
B
6. 如图,M是线段AB的中点,N是线段AM上一点,则下列结论不一定成立的是( )
A.MN=BM-AN
B.MN= AB-AN
C.MN= AM
D.MN=BN-AM
C
7.如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由。
C
●
●
●
●
B
D
A
●
M
解:
则点M为购物中心的位置。
8.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
D
A
C
B
M
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
因为M是AD的中点,
所以AM=MD=5x,
所以BM=AM-AB=3x.
因为BM=6,
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
课堂小结
线段长短的比较与运算
线段长短的比较
线段的和差
度量法
叠合法
中点
思想方法
方程思想
分类思想
基本事实
两点间的距离
两点之间,线段最短
两点间的线段的长度
4.3 线段的长短比较
第四章 直线与角
知识回顾
1.基本事实:
经过两点有一条直线,且只有一条直线.
(两点确定一条直线)
2.表示直线,射线,线段的方法:
(1)用一个小写英文字母表示;(2)用线上的两个点表示.
线段a
线段AB(BA)
射线l或
射线OA
直线l
直线AB(BA)
情景导入
小明
小华
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
小明
小华
思考:你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
②让两个同学站在同一平地上,脚底平齐,观看
两人的头顶,直接比出高矮.
——叠合法.
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
获取新知
对于两条线段来说,该如何比较它们的大小呢?
可以用刻度尺来量出线段的长度,然后比较。
——度量法.
2.6 cm
1
2
3
5
4
6
7
8
0
3.6 cm
1
2
3
5
4
6
7
8
0
叠合法结论:
C
D
(A)
B
C
D
A
B
B
(A)
B
A
B
A
C
D
(A)
(B)
3. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.
<
1. 若点 A 与点 C 重合,点 B 与点 D ,那么 AB = CD.
重合
>
2. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB CD.
比较线段长短的两种方法
1、度量法——从“数值”的角度比较
2、叠合法—— 从“形”的角度比较
起点对齐,看终点
在直线上画出线段 AB=a ,再在 AB 的延长线上画线段
BC=b,线段 AC 就是 与 的和,记作 AC= . 如
果在 AB 上画线段 BD=b,那么线段 AD 就是 与 的差,
记作AD= .
a
b
a+b
a-b
a
b
A
B
C
D
a+b
a-b
a
b
b
A
B
M
思考:将一条绳子对折,使绳子的端点重合,说说你的感受.你能找到线段的中点吗?三等分点?四等分点?
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.类似的,还有线段的三等分点、四等分点等.
线段的三等分点
线段的四等分点
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
点 M , N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
备注:求线段的长度时,当题目中涉及到线段长度的比例或倍分关系时,通常可以设未知数,运用方程思想求解.
对线段的中点的认识:
(1)线段的中点是线段上的点,且把线段分成相等
的两条线段;
(2)一条线段的中点有且只有一个;
(3)如图,若M是AB的中点,则①AM=BM= AB;
②AB=2AM=2BM;③AM+BM=AB且AM=BM.反过来也成立.
思考:如图是连结A、B两点之间各种形状的线绳,如果将它们都展直,你能从中得到什么启发?
A·
·B
基本事实:两点之间的所有连线中,线段最短.
把原来弯曲的河道改直,A,B 两地间的河道长度有什么变化?
A,B 两地间的河道长度变短.
基本事实:两点之间的所有连线中,线段最短.
(即两点之间,线段最短)
两点之间线段的长度,叫做这两点之间的距离.
备注:距离不是线段.
线段是一个几何图形;
距离是一个量,它反映的是线段的长短.距离是一个数量且有长度单位.
A
B
例题讲解
例1 已知:线段AB =4,延长AB至点C,使AC = 11.点 D是AB的中点,点E是AC的中点.求DE的长.
如图,因为AB=4,点D为AB中点,故 AD = 2.
又因为AC = 11,点E为AC中点,AE=5.5.
故 DE= AE - AD = 5. 5 - 2 = 3. 5.
解:
例2 C为线段AB上一点,D是线段AC的中点,E为线段CB的中点,
AB=9cm,AC=5cm.
求:(1)AD的长;
(2)求DE的长.
解:(1)因为D是AC的中点,AC=5cm,
所以AD= AC=2.5cm.
(2)因为 CB=AB-AC=9-5=4cm,E是BC的中点,
所以CE= CB=2cm.
所以 DE=DC+CE=2.5+2=4.5cm
例3 直线a表示一条河,在河两侧有两个村庄A和B。要在河边建一个供水站C,使C到两村庄的距离之和最小。请找出C点的位置,并说明理由。
a
A
B
C
点C即为所求. 理由:两点之间,线段最短
在解决选择位置、求最短距离等问题时,通常利用“两点之间,线段最短”.
例4 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
解析:分以下两种情况进行讨论:
当点C在AB之间上,故AC=AB-BC=1cm;
当点C在AB的延长线上时,AC=AB+BC=9cm.
C
1.为了比较线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,结果点B在线段CD的延长线上,则( )
A.AB
C.AB=CD D.以上都不对
B
随堂演练
B
2 .如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
3. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
C
4.下列说法正确的是( )
A.若AC= AB,则C是AB的中点
B.若AB=2CB,则C是AB的中点
C.若AC=BC,则C是AB的中点
D.若AC=BC= AB,则C是AB的中点
D
C
5. 如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )
A. AC = CB B. AB = 2 AC
C. AC + CB = AB D. CB = AB
A
C
B
6. 如图,M是线段AB的中点,N是线段AM上一点,则下列结论不一定成立的是( )
A.MN=BM-AN
B.MN= AB-AN
C.MN= AM
D.MN=BN-AM
C
7.如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由。
C
●
●
●
●
B
D
A
●
M
解:
则点M为购物中心的位置。
8.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
D
A
C
B
M
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
因为M是AD的中点,
所以AM=MD=5x,
所以BM=AM-AB=3x.
因为BM=6,
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
课堂小结
线段长短的比较与运算
线段长短的比较
线段的和差
度量法
叠合法
中点
思想方法
方程思想
分类思想
基本事实
两点间的距离
两点之间,线段最短
两点间的线段的长度
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
