沪科版数学七年级上册 4.5 第2课时 补角、余角 同步课件(共22张)
文档属性
| 名称 | 沪科版数学七年级上册 4.5 第2课时 补角、余角 同步课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 329.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 09:12:06 | ||
图片预览

文档简介
(共22张PPT)
第四章 直线与角
4.5 第2课时 余角和补角
情景导入
O
A
B
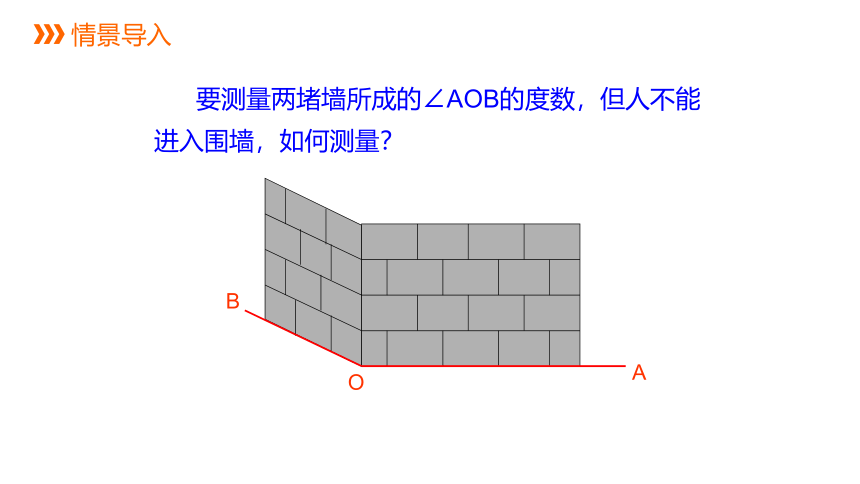
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
获取新知
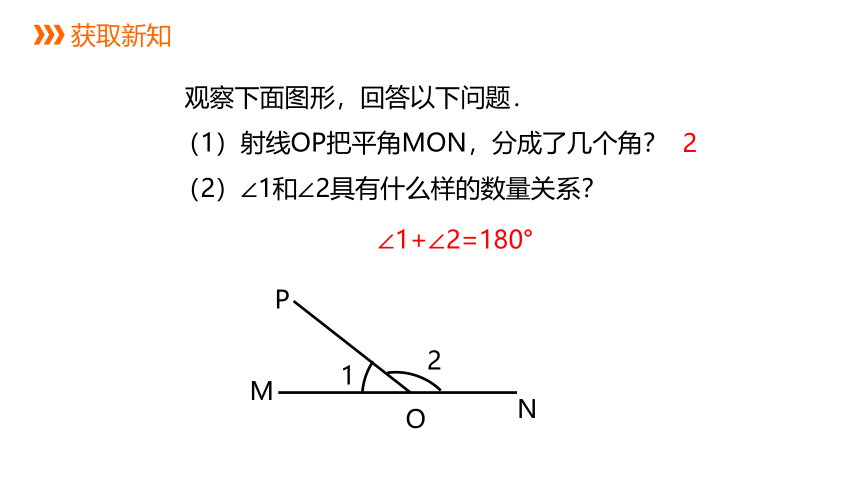
观察下面图形,回答以下问题.
(1)射线OP把平角MON,分成了几个角?
(2)∠1和∠2具有什么样的数量关系?
∠1+∠2=180°
2
P
M
O
N
1
2
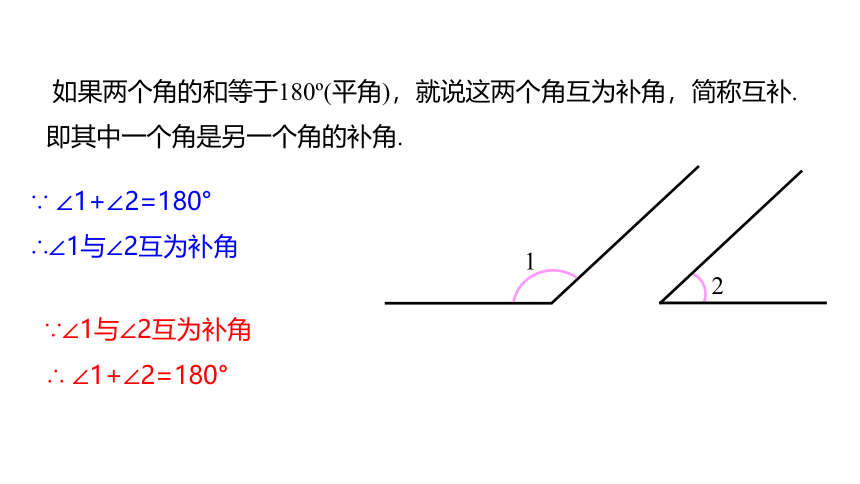
如果两个角的和等于180 (平角),就说这两个角互为补角,简称互补.即其中一个角是另一个角的补角.
1
2
∵ ∠1+∠2=180°
∴∠1与∠2互为补角
∵∠1与∠2互为补角
∴ ∠1+∠2=180°
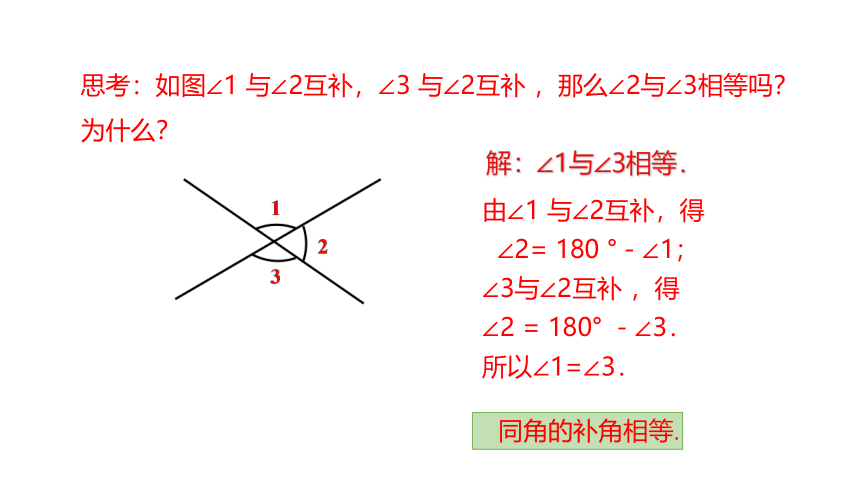
思考:如图∠1 与∠2互补,∠3 与∠2互补 ,那么∠2与∠3相等吗?为什么?
由∠1 与∠2互补,得
∠2= 180 °-∠1;
∠3与∠2互补 ,得
∠2 = 180° -∠3.
所以∠1=∠3.
解:∠1与∠3相等.
同角的补角相等.
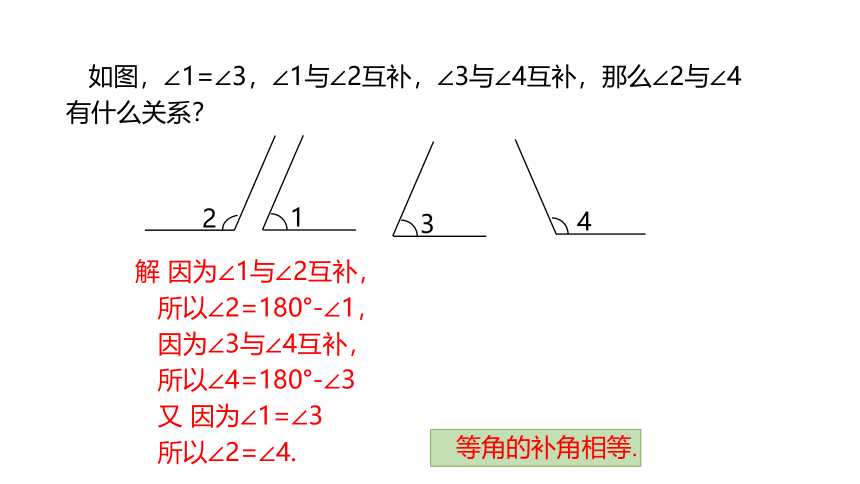
如图,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什么关系?
2
1
4
3
解 因为∠1与∠2互补,
所以∠2=180°-∠1,
因为∠3与∠4互补,
所以∠4=180°-∠3
又 因为∠1=∠3
所以∠2=∠4.
等角的补角相等.
P
A
O
B
1
2
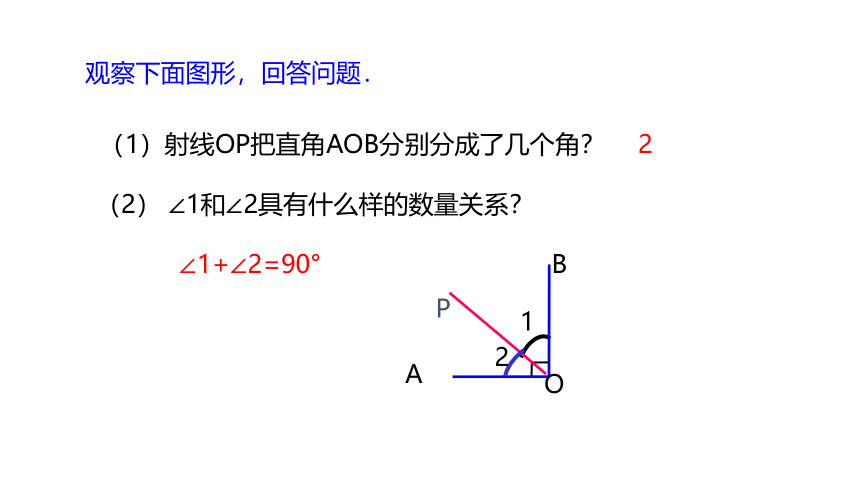
∠1+∠2=90°
观察下面图形,回答问题.
(1)射线OP把直角AOB分别分成了几个角?
(2) ∠1和∠2具有什么样的数量关系?
2
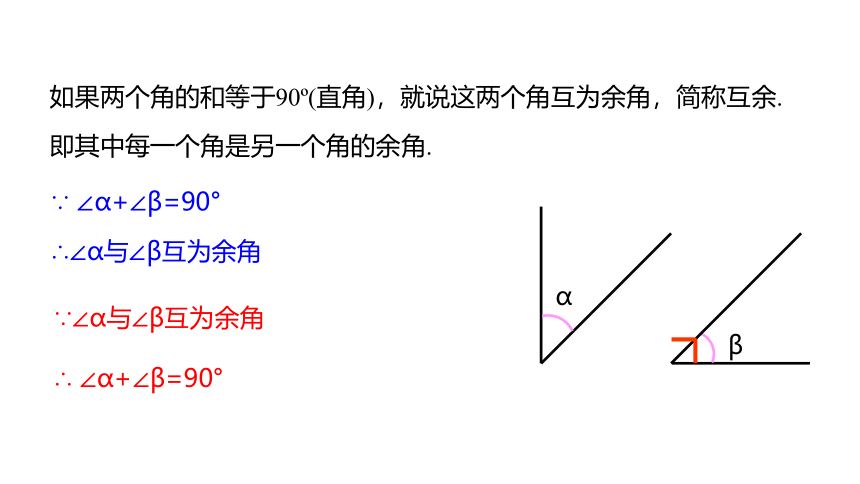
如果两个角的和等于90 (直角),就说这两个角互为余角,简称互余.
即其中每一个角是另一个角的余角.
∵ ∠α+∠β=90°
∴∠α与∠β互为余角
∵∠α与∠β互为余角
∴ ∠α+∠β=90°
α
β
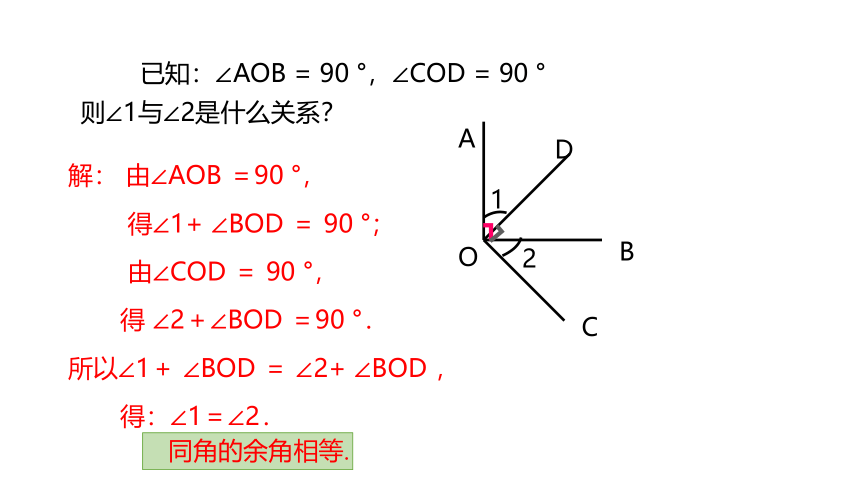
解: 由∠AOB =90 °,
得∠1+ ∠BOD = 90 °;
由∠COD = 90 °,
得 ∠2+∠BOD =90 °.
所以∠1+ ∠BOD = ∠2+ ∠BOD ,
得:∠1=∠2.
已知:∠AOB = 90 °,∠COD = 90 °
则∠1与∠2是什么关系?
A
O
B
C
D
1
2
┓
┓
同角的余角相等.
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
解:∠2与∠4相等.
由∠1 与∠2互余,可得 ∠1= 90 °-∠2,
由∠3与∠4互余 ,可得 ∠3=90°- ∠4.
又因为∠1=∠3,
所以90 °-∠2= 90°- ∠4
可得∠2=∠4.
等角的余角相等.
如果 ∠1 与∠2互余,那么∠1 的余角是∠2,同样∠2的余角是∠1 ; 如果∠1 与∠2互补,那么∠1 的补角是∠2, 同样∠2的补角是∠1 。
两角互余或互补,只与角的度数有关,与位置无关。
思考1:定义中的“互为”一词如何理解?
思考2:互余、互补的两角是否一定有公共顶点或公共边?
备注:互余,互补必须是两个角之间的关系.
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
1
2
1
2
例1 如图,点A,O, B在同一条直线 上,射线OD和射线
OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
解:因为点A,O, B在同一条直线上,
所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,
∠COD和∠BOE也互为余角.
O
A
B
C
D
E
例题讲解
例2 已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则 ∠A 的度数为(3x+30)°.
根据题意得:
x + ( 3x+30 ) = 90.
解得 x=15.
故 ∠B 的度数为15°.
我们在求有关图形的角度问题时,通常把一个角设为未知数,表示出其他角,进而利用方程求解,这时我们用到的便是方程思想.
随堂演练
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
2.如果一个角是56°,那么下列说法中正确的是( )
A.它的余角是44° B.它的补角是44°
C.它的余角是124° D.它的补角是124°
D
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
C
4. 如图,下面说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70°
C
5. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
6. 一个角的补角比它的余角的3倍小20°,求这个角的度数.
解:设这个角的度数为x°.
由题意,得180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°.
7. 如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角?
解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,
∠1与∠BDE,∠EDC与∠FDC互为补角.
课堂小结
余角和补角
余角
补角
两个角的和等于90
两个角的和等于180
定义
性质
同(等)角的余角相等
定义
性质
同(等)角的补角相等
第四章 直线与角
4.5 第2课时 余角和补角
情景导入
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
获取新知
观察下面图形,回答以下问题.
(1)射线OP把平角MON,分成了几个角?
(2)∠1和∠2具有什么样的数量关系?
∠1+∠2=180°
2
P
M
O
N
1
2
如果两个角的和等于180 (平角),就说这两个角互为补角,简称互补.即其中一个角是另一个角的补角.
1
2
∵ ∠1+∠2=180°
∴∠1与∠2互为补角
∵∠1与∠2互为补角
∴ ∠1+∠2=180°
思考:如图∠1 与∠2互补,∠3 与∠2互补 ,那么∠2与∠3相等吗?为什么?
由∠1 与∠2互补,得
∠2= 180 °-∠1;
∠3与∠2互补 ,得
∠2 = 180° -∠3.
所以∠1=∠3.
解:∠1与∠3相等.
同角的补角相等.
如图,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什么关系?
2
1
4
3
解 因为∠1与∠2互补,
所以∠2=180°-∠1,
因为∠3与∠4互补,
所以∠4=180°-∠3
又 因为∠1=∠3
所以∠2=∠4.
等角的补角相等.
P
A
O
B
1
2
∠1+∠2=90°
观察下面图形,回答问题.
(1)射线OP把直角AOB分别分成了几个角?
(2) ∠1和∠2具有什么样的数量关系?
2
如果两个角的和等于90 (直角),就说这两个角互为余角,简称互余.
即其中每一个角是另一个角的余角.
∵ ∠α+∠β=90°
∴∠α与∠β互为余角
∵∠α与∠β互为余角
∴ ∠α+∠β=90°
α
β
解: 由∠AOB =90 °,
得∠1+ ∠BOD = 90 °;
由∠COD = 90 °,
得 ∠2+∠BOD =90 °.
所以∠1+ ∠BOD = ∠2+ ∠BOD ,
得:∠1=∠2.
已知:∠AOB = 90 °,∠COD = 90 °
则∠1与∠2是什么关系?
A
O
B
C
D
1
2
┓
┓
同角的余角相等.
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
解:∠2与∠4相等.
由∠1 与∠2互余,可得 ∠1= 90 °-∠2,
由∠3与∠4互余 ,可得 ∠3=90°- ∠4.
又因为∠1=∠3,
所以90 °-∠2= 90°- ∠4
可得∠2=∠4.
等角的余角相等.
如果 ∠1 与∠2互余,那么∠1 的余角是∠2,同样∠2的余角是∠1 ; 如果∠1 与∠2互补,那么∠1 的补角是∠2, 同样∠2的补角是∠1 。
两角互余或互补,只与角的度数有关,与位置无关。
思考1:定义中的“互为”一词如何理解?
思考2:互余、互补的两角是否一定有公共顶点或公共边?
备注:互余,互补必须是两个角之间的关系.
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
1
2
1
2
例1 如图,点A,O, B在同一条直线 上,射线OD和射线
OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
解:因为点A,O, B在同一条直线上,
所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,
∠COD和∠BOE也互为余角.
O
A
B
C
D
E
例题讲解
例2 已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则 ∠A 的度数为(3x+30)°.
根据题意得:
x + ( 3x+30 ) = 90.
解得 x=15.
故 ∠B 的度数为15°.
我们在求有关图形的角度问题时,通常把一个角设为未知数,表示出其他角,进而利用方程求解,这时我们用到的便是方程思想.
随堂演练
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
2.如果一个角是56°,那么下列说法中正确的是( )
A.它的余角是44° B.它的补角是44°
C.它的余角是124° D.它的补角是124°
D
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
C
4. 如图,下面说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70°
C
5. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
6. 一个角的补角比它的余角的3倍小20°,求这个角的度数.
解:设这个角的度数为x°.
由题意,得180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°.
7. 如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角?
解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,
∠1与∠BDE,∠EDC与∠FDC互为补角.
课堂小结
余角和补角
余角
补角
两个角的和等于90
两个角的和等于180
定义
性质
同(等)角的余角相等
定义
性质
同(等)角的补角相等
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
