双曲线的几何性质
图片预览






文档简介
课件24张PPT。 双曲线的几何性质 一、知识再现
前面我们学习了椭圆 的简单的几何性质: 范围、对称性、顶点、离心率.
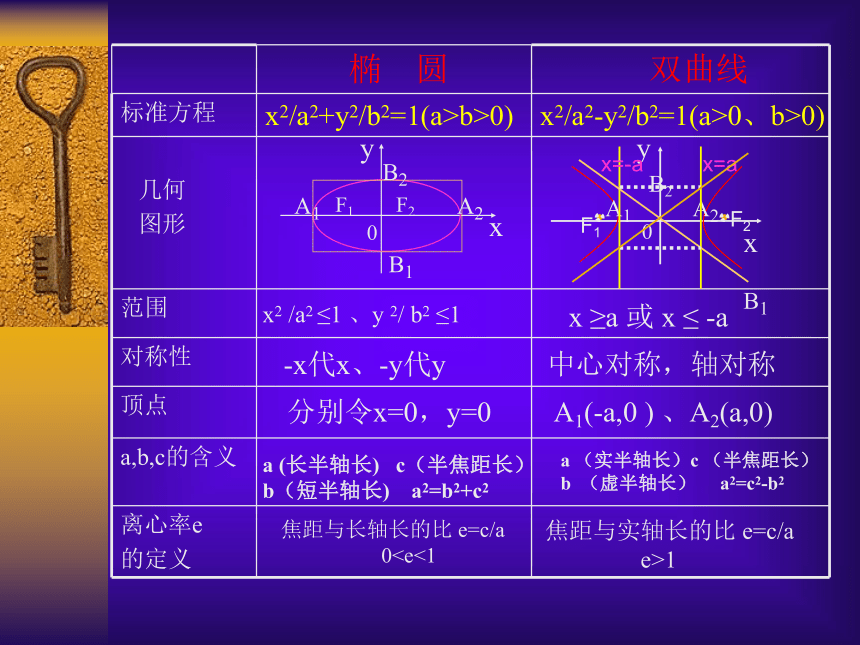
我们来共同回顾一下椭圆 x2/a2+y2/b2=1(a>b>0)
几何性质的具体内容及其研究方法.|x |≤a 、|y |≤ b x2/ a2 ≤1 、y 2/ b2 ≤1中心对称,轴对称 -x代x、-y代yA1(-a,0 ) , A2(a,0)
B1(0-b ) , B2(0,b)分别令x=0,y=0a (长半轴长) c(半焦距长)
b(短半轴长) a2=b2+c2焦距与长轴长的比 e=c/a
0
我们能否用研究椭圆的几何性质的方法来研究双曲线的几何性质呢?
x2 /a2 ≤1 、y 2/ b2 ≤1 -x代x、-y代y分别令x=0,y=0 x ≥a 或 x ≤ -a中心对称,轴对称A1(-a,0 ) 、A2(a,0)a (实半轴长)c (半焦距长)
b (虚半轴长) a2=c2-b2焦距与实轴长的比 e=c/a
e>1a (长半轴长) c(半焦距长)
b(短半轴长) a2=b2+c2焦距与长轴长的比 e=c/a
0
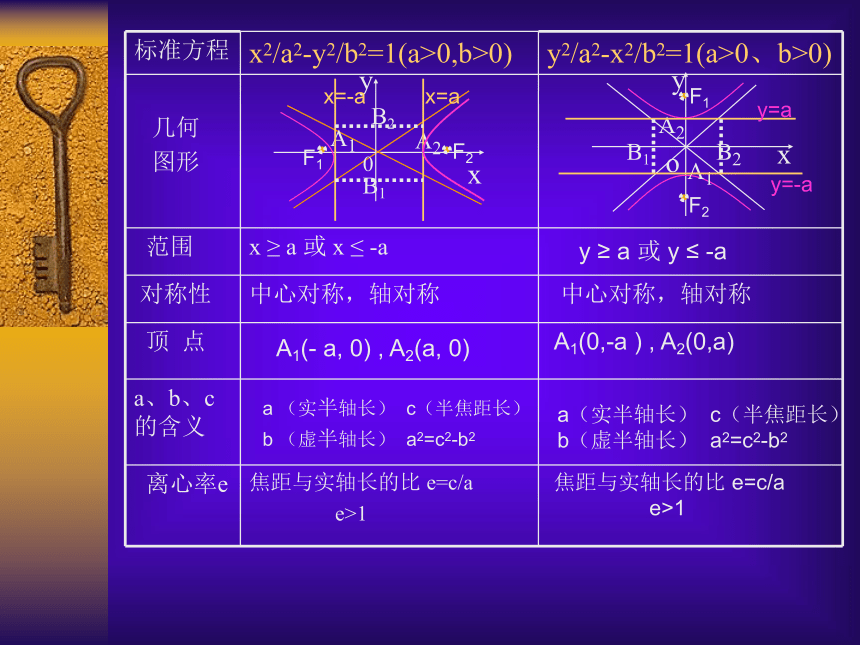
我们已经研究了焦点在x轴上的双曲线的几何性质,那么当焦点在y轴上的双曲线的几何性质又如何呢?
y ≥ a 或 y ≤ -a中心对称,轴对称A1(0,-a ) , A2(0,a)A1(- a, 0) , A2(a, 0)a(实半轴长) c(半焦距长)
b(虚半轴长) a2=c2-b2a (实半轴长) c(半焦距长)
b (虚半轴长) a2=c2-b2焦距与实轴长的比 e=c/a
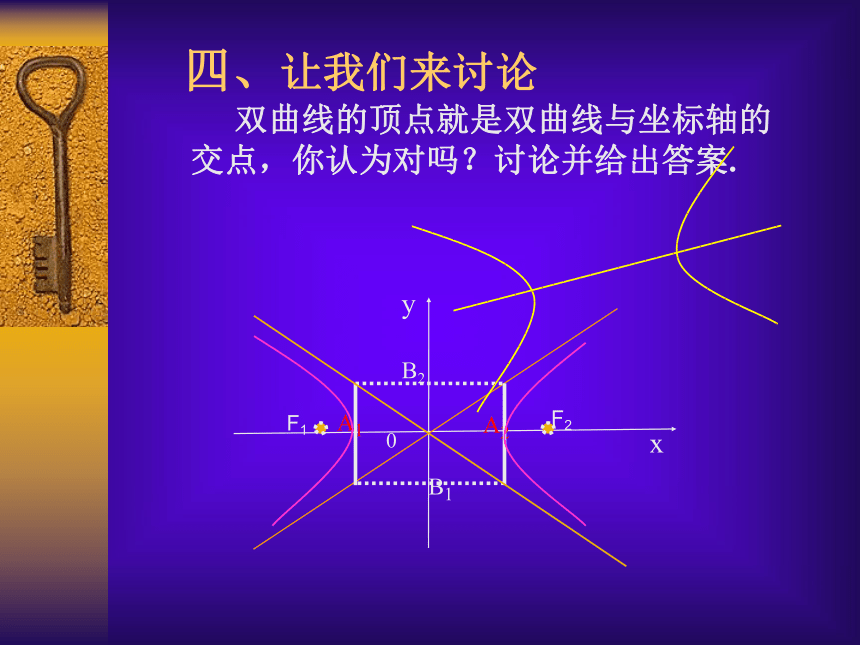
e>1 yx oA2A1 B1B2F1 F2yF2A2A1B2 0xF1x=ax=-ay=ay=-a B1 四、让我们来讨论
双曲线的顶点就是双曲线与坐标轴的交点,你认为对吗?讨论并给出答案.yF2B1
A2A1B2 0xF1五、让我们共同分析 例1、求双曲线 9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率. 分析:
①化为标准方程: y2/16-x2/9=1 ②确定焦点位置:在y轴上 ③找出a、b的值:a=4,b=3 ④代入关系式c2=a2+b2=25 、e=c/a=5/4 ⑤写出结果:a=4,b=3,F1(0, 5),F2(0,-5),e=5/4.
六、练一练 求下列双曲线的实半轴长和虚半轴长及顶点坐标.
(1)x2-4y2=16 (2) x2/49-y2/25=-1 解答:(1)a=4,b=2,A1(-4,0),A2(4,0)
(2)a=5,b=7,A1(0,-5),A2(0,5)请思考:如若求半焦距长和离心率呢? 小结:关键在于求实半轴a的长和虚半轴b的长,然后代入关系式c2=a2+b2、e=c/a求半焦距c的长及离心率.七、让我们继续研究请观察双曲线的图象和矩形对角线,有何特征? 双曲线 x2/a2-y2/b2=1(a>0、b>0)的各支向外延伸时,与矩形的两条对角线所在的直线逐渐接近.请思考:结论正确吗?F2 yB1A2A1
B2 0 xF1(一)、我们共同来设计一个方案:八、我们一起来证明 1、由双曲线的对称性我们只需研究第一象限的情形; 2、如何说明双曲线 x2/a2-y2/b2=1在第一象限内与矩形的对角线所在的直线逐渐接近且不相交呢? M(x,y) Q(2)如何说明|MQ|逐渐减小且不等于0呢?0xybaLN(x,Y)(3)如何证明|MN|逐渐减小且不等于0呢?我们可用方程的思想解决:
|MN|=Y- y,求出M、N点坐标即可.为此我们过点M作一条直线L与y轴平行,交矩形对角线与N点,坐标记为N( x ,Y).我们需证明N点在M点上方,即证y < Y.又|MQ| < |MN| ,所只需证明|MN|逐渐减小且不等于0即可.(1)我们在第一象限内双曲线图象上任取一点M(x, y ),过M点向矩形的对角线y=bx/a引垂线,垂足为Q点。我们只需说明|MQ|逐渐减小且不等于0即可.(二)、我们来证明 先取双曲线在第一象限内的部分进行证明这一部分的方程可写为 0xyN(x,Y) QM(x,y) 在该式子中x (x≥a)逐渐增大时,
|MN|逐渐减小且不等于0.
又|MQ| <|MN|,所以|MQ|逐渐减小且不等于0.即双曲线 x2/a2-y2/b2=1在第一象限内与矩形的对角线所在的直线逐渐接近且不相交.在其它象限内,我们可类似证明. yN(x,Y)M(x,y)(三)、请注意:1、当焦点在y轴上时也可类似证明具有同样性质; 2、我们把两条直线 y =±bx /a 叫做双曲线的渐近线.3、当焦点在x轴上时,方程为 x2/a2-y2/b2=1(a>0,b>0),渐
近线方程为y =±bx /a ;
当焦点在y轴上时,方程为y2/a2- x2/b2=1(a>0,b>0),渐近
线方程为y =±ax /b .九、动脑筋1、如何求双曲线的渐近线?
例:求下列双曲线 的渐近线
(1) 9y2-16x2=144;
(2) 9y2-16x2= -144 . 规律总结:
(1)求矩形对角线所在的直线方程;解答:(1)y=±4x/3 , (2)y=±4x/30yba (2)化成标准式后再将1换成0或直接将常数项换为0.2、双曲线与其渐近线之间是否是一对一关系?例:当渐近线方程为y=±bx/a时,双曲线的标准方
程一定是x2/a2-y2/b2=1吗?为什么?xy=bx/ay=-bx/a3、类比作椭圆的简图,如何较规范地作出双曲线的图形? 例:画出下列双曲线的图形
(1) 9y2-16x2=144;
(2) x2 -y2= 4 .注:实轴和虚轴等长的双曲线
叫做等轴双曲线.M- 3 3 4 - 4十、让我们来共同回顾 本节课我们共同学习了那些内容: yF2B1A2A1B2 0xF1X=aX=-ayF2B1A2A1B2 0xF1X=aX=-a yx oA2A1 B1B2F1 F2 双曲线的渐近线 当焦点在x轴上时,方程为 x2/a2-y2/b2=1(a>0,b>0),渐
近线方程为y =±bx /a ;
当焦点在y轴上时,方程为 y2/a2-x2/b2=1(a>0,b>0),渐近
线方程为y =±ax /b .B1A2A1B2 0xF1X=aX=-a 1、离心率e的变化对双曲线图形有何影响? 如何解释? 十一、课后请你思考题0ybaF1CF2x0ye1e2e3e4 2、 如图,双曲线和椭圆的离心率分别为e1、e2、e3、e4, 试比较e1、e2、e3、e4 的大小.再见!
前面我们学习了椭圆 的简单的几何性质: 范围、对称性、顶点、离心率.
我们来共同回顾一下椭圆 x2/a2+y2/b2=1(a>b>0)
几何性质的具体内容及其研究方法.|x |≤a 、|y |≤ b x2/ a2 ≤1 、y 2/ b2 ≤1中心对称,轴对称 -x代x、-y代yA1(-a,0 ) , A2(a,0)
B1(0-b ) , B2(0,b)分别令x=0,y=0a (长半轴长) c(半焦距长)
b(短半轴长) a2=b2+c2焦距与长轴长的比 e=c/a
0
我们能否用研究椭圆的几何性质的方法来研究双曲线的几何性质呢?
x2 /a2 ≤1 、y 2/ b2 ≤1 -x代x、-y代y分别令x=0,y=0 x ≥a 或 x ≤ -a中心对称,轴对称A1(-a,0 ) 、A2(a,0)a (实半轴长)c (半焦距长)
b (虚半轴长) a2=c2-b2焦距与实轴长的比 e=c/a
e>1a (长半轴长) c(半焦距长)
b(短半轴长) a2=b2+c2焦距与长轴长的比 e=c/a
0
我们已经研究了焦点在x轴上的双曲线的几何性质,那么当焦点在y轴上的双曲线的几何性质又如何呢?
y ≥ a 或 y ≤ -a中心对称,轴对称A1(0,-a ) , A2(0,a)A1(- a, 0) , A2(a, 0)a(实半轴长) c(半焦距长)
b(虚半轴长) a2=c2-b2a (实半轴长) c(半焦距长)
b (虚半轴长) a2=c2-b2焦距与实轴长的比 e=c/a
e>1 yx oA2A1 B1B2F1 F2yF2A2A1B2 0xF1x=ax=-ay=ay=-a B1 四、让我们来讨论
双曲线的顶点就是双曲线与坐标轴的交点,你认为对吗?讨论并给出答案.yF2B1
A2A1B2 0xF1五、让我们共同分析 例1、求双曲线 9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率. 分析:
①化为标准方程: y2/16-x2/9=1 ②确定焦点位置:在y轴上 ③找出a、b的值:a=4,b=3 ④代入关系式c2=a2+b2=25 、e=c/a=5/4 ⑤写出结果:a=4,b=3,F1(0, 5),F2(0,-5),e=5/4.
六、练一练 求下列双曲线的实半轴长和虚半轴长及顶点坐标.
(1)x2-4y2=16 (2) x2/49-y2/25=-1 解答:(1)a=4,b=2,A1(-4,0),A2(4,0)
(2)a=5,b=7,A1(0,-5),A2(0,5)请思考:如若求半焦距长和离心率呢? 小结:关键在于求实半轴a的长和虚半轴b的长,然后代入关系式c2=a2+b2、e=c/a求半焦距c的长及离心率.七、让我们继续研究请观察双曲线的图象和矩形对角线,有何特征? 双曲线 x2/a2-y2/b2=1(a>0、b>0)的各支向外延伸时,与矩形的两条对角线所在的直线逐渐接近.请思考:结论正确吗?F2 yB1A2A1
B2 0 xF1(一)、我们共同来设计一个方案:八、我们一起来证明 1、由双曲线的对称性我们只需研究第一象限的情形; 2、如何说明双曲线 x2/a2-y2/b2=1在第一象限内与矩形的对角线所在的直线逐渐接近且不相交呢? M(x,y) Q(2)如何说明|MQ|逐渐减小且不等于0呢?0xybaLN(x,Y)(3)如何证明|MN|逐渐减小且不等于0呢?我们可用方程的思想解决:
|MN|=Y- y,求出M、N点坐标即可.为此我们过点M作一条直线L与y轴平行,交矩形对角线与N点,坐标记为N( x ,Y).我们需证明N点在M点上方,即证y < Y.又|MQ| < |MN| ,所只需证明|MN|逐渐减小且不等于0即可.(1)我们在第一象限内双曲线图象上任取一点M(x, y ),过M点向矩形的对角线y=bx/a引垂线,垂足为Q点。我们只需说明|MQ|逐渐减小且不等于0即可.(二)、我们来证明 先取双曲线在第一象限内的部分进行证明这一部分的方程可写为 0xyN(x,Y) QM(x,y) 在该式子中x (x≥a)逐渐增大时,
|MN|逐渐减小且不等于0.
又|MQ| <|MN|,所以|MQ|逐渐减小且不等于0.即双曲线 x2/a2-y2/b2=1在第一象限内与矩形的对角线所在的直线逐渐接近且不相交.在其它象限内,我们可类似证明. yN(x,Y)M(x,y)(三)、请注意:1、当焦点在y轴上时也可类似证明具有同样性质; 2、我们把两条直线 y =±bx /a 叫做双曲线的渐近线.3、当焦点在x轴上时,方程为 x2/a2-y2/b2=1(a>0,b>0),渐
近线方程为y =±bx /a ;
当焦点在y轴上时,方程为y2/a2- x2/b2=1(a>0,b>0),渐近
线方程为y =±ax /b .九、动脑筋1、如何求双曲线的渐近线?
例:求下列双曲线 的渐近线
(1) 9y2-16x2=144;
(2) 9y2-16x2= -144 . 规律总结:
(1)求矩形对角线所在的直线方程;解答:(1)y=±4x/3 , (2)y=±4x/30yba (2)化成标准式后再将1换成0或直接将常数项换为0.2、双曲线与其渐近线之间是否是一对一关系?例:当渐近线方程为y=±bx/a时,双曲线的标准方
程一定是x2/a2-y2/b2=1吗?为什么?xy=bx/ay=-bx/a3、类比作椭圆的简图,如何较规范地作出双曲线的图形? 例:画出下列双曲线的图形
(1) 9y2-16x2=144;
(2) x2 -y2= 4 .注:实轴和虚轴等长的双曲线
叫做等轴双曲线.M- 3 3 4 - 4十、让我们来共同回顾 本节课我们共同学习了那些内容: yF2B1A2A1B2 0xF1X=aX=-ayF2B1A2A1B2 0xF1X=aX=-a yx oA2A1 B1B2F1 F2 双曲线的渐近线 当焦点在x轴上时,方程为 x2/a2-y2/b2=1(a>0,b>0),渐
近线方程为y =±bx /a ;
当焦点在y轴上时,方程为 y2/a2-x2/b2=1(a>0,b>0),渐近
线方程为y =±ax /b .B1A2A1B2 0xF1X=aX=-a 1、离心率e的变化对双曲线图形有何影响? 如何解释? 十一、课后请你思考题0ybaF1CF2x0ye1e2e3e4 2、 如图,双曲线和椭圆的离心率分别为e1、e2、e3、e4, 试比较e1、e2、e3、e4 的大小.再见!
