直线的倾斜角与斜率
图片预览






文档简介
课件15张PPT。直线的倾斜角与斜率目的要求:
1、初步了解“直线的方程”和“方程的直线”概念;
2、了解直线的倾斜角概念,理解直线的斜率概念,并能准确表述直线的倾斜角的定义;
3、已知直线倾斜角(或斜率)会求直线的斜率(或倾斜角);
4、培养和提高学生的联想、对应、转化等辨证思维。
教学重点、难点:
本节的重点是直线的倾斜角斜率的概念;
难点是斜率存在与不存在的讨论及用反三角函数表示直线的倾斜角。教学过程:1、“直线的方程”和“方程的直线”oB(1,3)xyA(0,1)y=2x+1 (1)有序数对(0,1)满足函数y=2x+1,
则直线上就有一点A,它的坐标是(0,1)。 (2)反过来,直线上点B(1,3),则有序实数对(1,3)就满足y=2x+1。 一般地,满足函数式y=kx+b的每一对x,y的值,都是直线 上的点的坐标(x,y);反之,直线 上每一点的坐标(x,y)都满足函数式y=kx+b,因此,一次函数y=kx+b的图象是一条直线,它是以满足y=kx+b的每一对x,y的值为坐标的点构成的。
从方程的角度看,函数y=kx+b也可以看作是二元一次方程y-kx-b=0,这样满足一次函数y=kx+b的每一对x,y的值“变成了”二元一次方程y-kx-b=0的解,使方程和直线建立了联系。定义:以一个方程的解为坐标的点都是某条直线上的点,反过来,这条直线上的所有点坐标都是这个方程的解,这时,这个方程就叫做这条直线的方程,这条直线就叫做这个方程的直线。以上定义改用集合表述:
直线可以看成由点组成的集合,记作C,以一个关于x,y的二元一次方程的解为坐标的集合,记作F。
若(1)C F(2)F C,则C=F(3)点( ,1)不在直线 上。(0,-2)(-3,0)例1、已知方程2x+3y+6=0。
(1)把这个方程改成一次函数式;
(2)画出这个方程所对应的直线 。
(3)点( ,1)是否在直线 上。略解:(1)(2)过A(0,-2),B(-3,0)
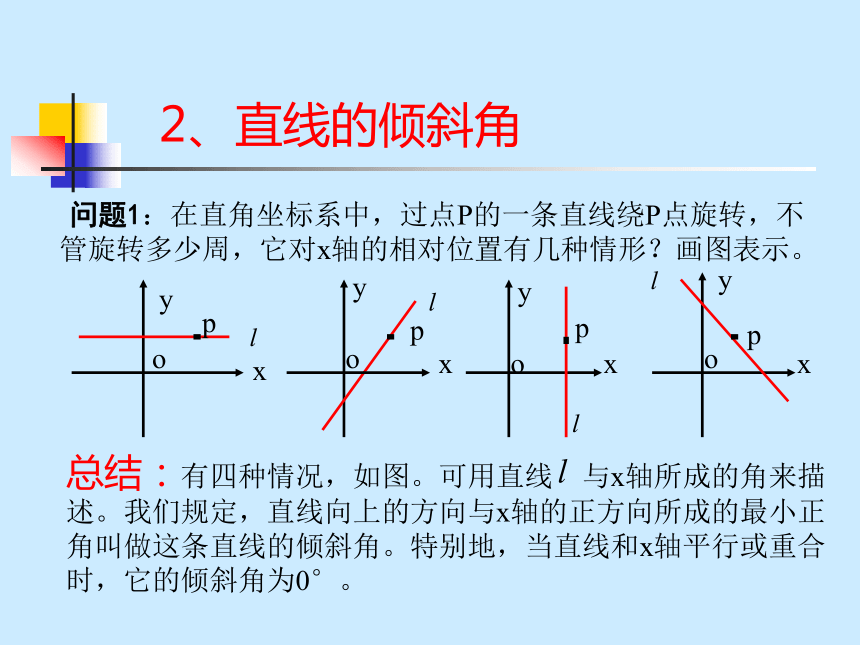
两点的直线即为所求直线 ;2、直线的倾斜角 问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。总结:有四种情况,如图。可用直线 与x轴所成的角来描述。我们规定,直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。特别地,当直线和x轴平行或重合时,它的倾斜角为0°。定义:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕着交点按逆时针方向旋转到与直线重合时所转的最小正角,记为 那么就叫做直线的倾斜角。问题2:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?问题3:直线的倾斜角能不能是0°?能不能是锐角?能不能是直角?能不能是钝角?能不能是平角?能否大于平角?(通过问题3的分析可知倾斜角的取值范围是0°≤ <180°,在此范围内,坐标平面上的任何一条直线都有唯一的倾斜角。而每一个倾斜角都能确定一条直线的方向,倾斜角直观地表示了直线对x轴正方向的倾斜程度。)提问:3、直线的斜率给出一个描述直线方程的量——直线的斜率定义3:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。斜率通常用k表示,即:问题4:当 =0°时,k值如何?
当0°< < 90°时,k值如何?
当 =90°时,k值如何?
当90° < <180°时,k值如何?问题5:填表说出直线的倾斜角与斜率k之间的关系:
例2:直线 的倾斜角 =30°,直线 ,
求 , 的斜率。解: 的斜率为
的倾斜角为
的斜率为例3:如图所示菱形ABCD的 BAD=60°,求菱形ABCD各边和两条对角线所在直线的倾斜角和斜率。略解:5、小结:4、课堂练习:
(1)课本第37面练习1、2。
(2)直线的倾斜角 的正切值为 ,求此直线的斜率。思考题:
(1)如果直线 的斜率为0, ,那么直线 的斜率怎样?
(2)如果直线 的斜率 的范围是 ,那么它的倾斜角的范 围是什么?
(3)直线的倾斜角的正弦为 ,也是 的三角函数,为什么不用 它来作直线的斜率呢?6、布置作业:
(1)阅读教材第35面至第37面。
(2)第37页习题7.1第1、2、3题。谢谢指导黄山市徽州区第一中学
凌荣寿
1、初步了解“直线的方程”和“方程的直线”概念;
2、了解直线的倾斜角概念,理解直线的斜率概念,并能准确表述直线的倾斜角的定义;
3、已知直线倾斜角(或斜率)会求直线的斜率(或倾斜角);
4、培养和提高学生的联想、对应、转化等辨证思维。
教学重点、难点:
本节的重点是直线的倾斜角斜率的概念;
难点是斜率存在与不存在的讨论及用反三角函数表示直线的倾斜角。教学过程:1、“直线的方程”和“方程的直线”oB(1,3)xyA(0,1)y=2x+1 (1)有序数对(0,1)满足函数y=2x+1,
则直线上就有一点A,它的坐标是(0,1)。 (2)反过来,直线上点B(1,3),则有序实数对(1,3)就满足y=2x+1。 一般地,满足函数式y=kx+b的每一对x,y的值,都是直线 上的点的坐标(x,y);反之,直线 上每一点的坐标(x,y)都满足函数式y=kx+b,因此,一次函数y=kx+b的图象是一条直线,它是以满足y=kx+b的每一对x,y的值为坐标的点构成的。
从方程的角度看,函数y=kx+b也可以看作是二元一次方程y-kx-b=0,这样满足一次函数y=kx+b的每一对x,y的值“变成了”二元一次方程y-kx-b=0的解,使方程和直线建立了联系。定义:以一个方程的解为坐标的点都是某条直线上的点,反过来,这条直线上的所有点坐标都是这个方程的解,这时,这个方程就叫做这条直线的方程,这条直线就叫做这个方程的直线。以上定义改用集合表述:
直线可以看成由点组成的集合,记作C,以一个关于x,y的二元一次方程的解为坐标的集合,记作F。
若(1)C F(2)F C,则C=F(3)点( ,1)不在直线 上。(0,-2)(-3,0)例1、已知方程2x+3y+6=0。
(1)把这个方程改成一次函数式;
(2)画出这个方程所对应的直线 。
(3)点( ,1)是否在直线 上。略解:(1)(2)过A(0,-2),B(-3,0)
两点的直线即为所求直线 ;2、直线的倾斜角 问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。总结:有四种情况,如图。可用直线 与x轴所成的角来描述。我们规定,直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。特别地,当直线和x轴平行或重合时,它的倾斜角为0°。定义:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕着交点按逆时针方向旋转到与直线重合时所转的最小正角,记为 那么就叫做直线的倾斜角。问题2:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?问题3:直线的倾斜角能不能是0°?能不能是锐角?能不能是直角?能不能是钝角?能不能是平角?能否大于平角?(通过问题3的分析可知倾斜角的取值范围是0°≤ <180°,在此范围内,坐标平面上的任何一条直线都有唯一的倾斜角。而每一个倾斜角都能确定一条直线的方向,倾斜角直观地表示了直线对x轴正方向的倾斜程度。)提问:3、直线的斜率给出一个描述直线方程的量——直线的斜率定义3:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。斜率通常用k表示,即:问题4:当 =0°时,k值如何?
当0°< < 90°时,k值如何?
当 =90°时,k值如何?
当90° < <180°时,k值如何?问题5:填表说出直线的倾斜角与斜率k之间的关系:
例2:直线 的倾斜角 =30°,直线 ,
求 , 的斜率。解: 的斜率为
的倾斜角为
的斜率为例3:如图所示菱形ABCD的 BAD=60°,求菱形ABCD各边和两条对角线所在直线的倾斜角和斜率。略解:5、小结:4、课堂练习:
(1)课本第37面练习1、2。
(2)直线的倾斜角 的正切值为 ,求此直线的斜率。思考题:
(1)如果直线 的斜率为0, ,那么直线 的斜率怎样?
(2)如果直线 的斜率 的范围是 ,那么它的倾斜角的范 围是什么?
(3)直线的倾斜角的正弦为 ,也是 的三角函数,为什么不用 它来作直线的斜率呢?6、布置作业:
(1)阅读教材第35面至第37面。
(2)第37页习题7.1第1、2、3题。谢谢指导黄山市徽州区第一中学
凌荣寿
