19.1.2平行四边形判定 课件
文档属性
| 名称 | 19.1.2平行四边形判定 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-20 22:00:09 | ||
图片预览



文档简介
课件31张PPT。20.2.3 平行四边形判定1马鞍山市金瑞中学数学初二备课组本节课学习目标1.掌握平行四边形的定义判定法及其推论.
2.理解定理1和定理2,并应用于平行四边形的判定中.自学内容:
课本77~79页
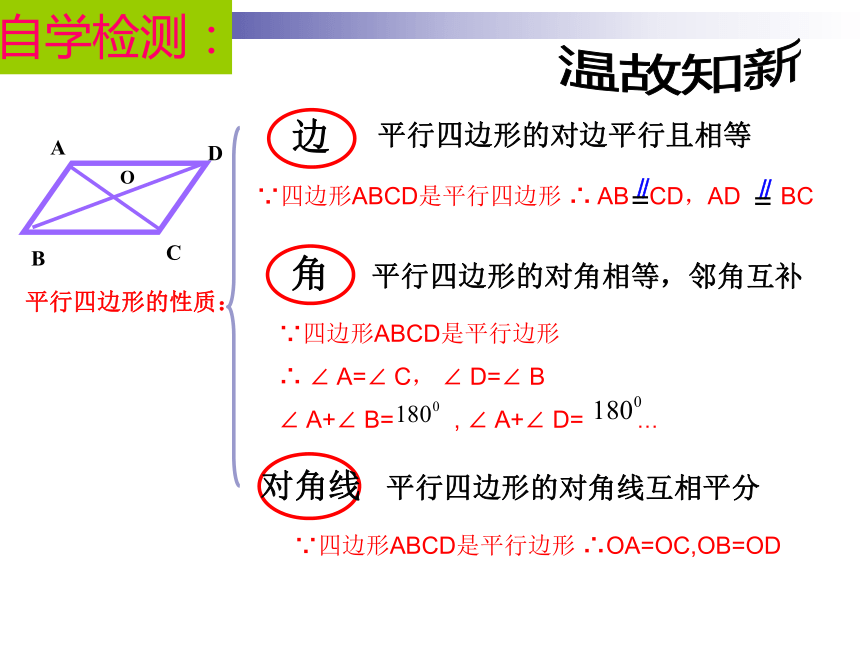
基础练习:平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
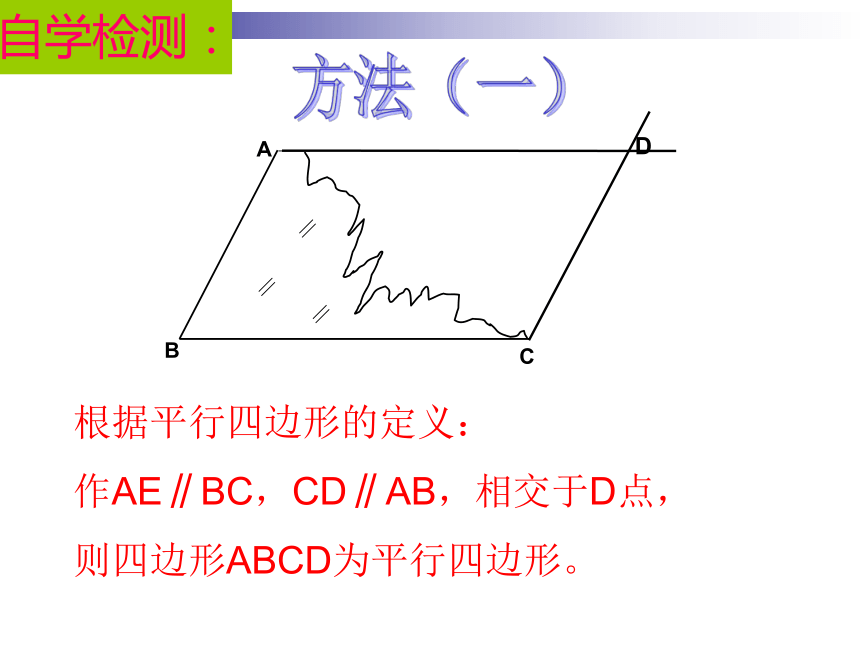
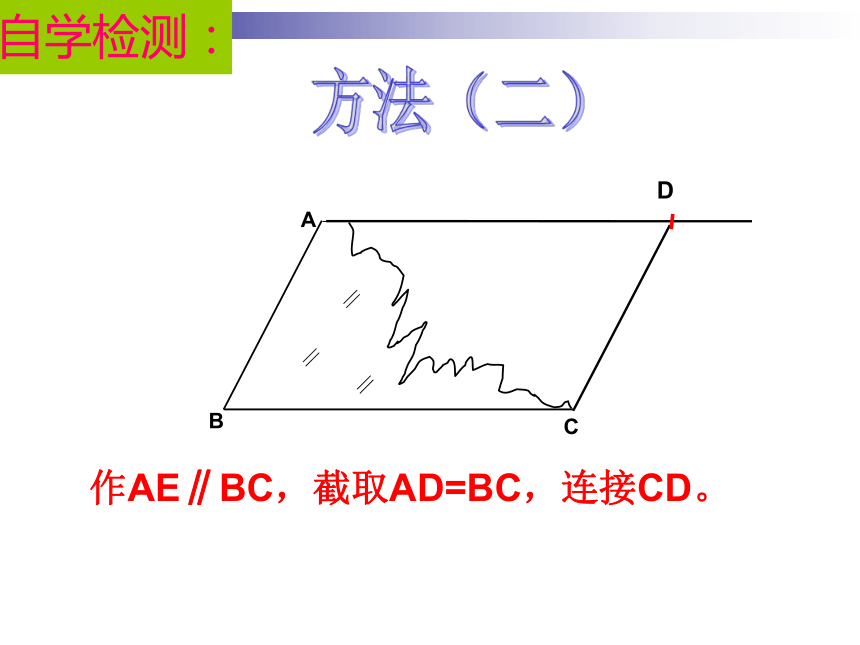
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD自学检测: 昨天初二的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战自学检测:方法(一)D根据平行四边形的定义:
作AE∥BC,CD∥AB,相交于D点,
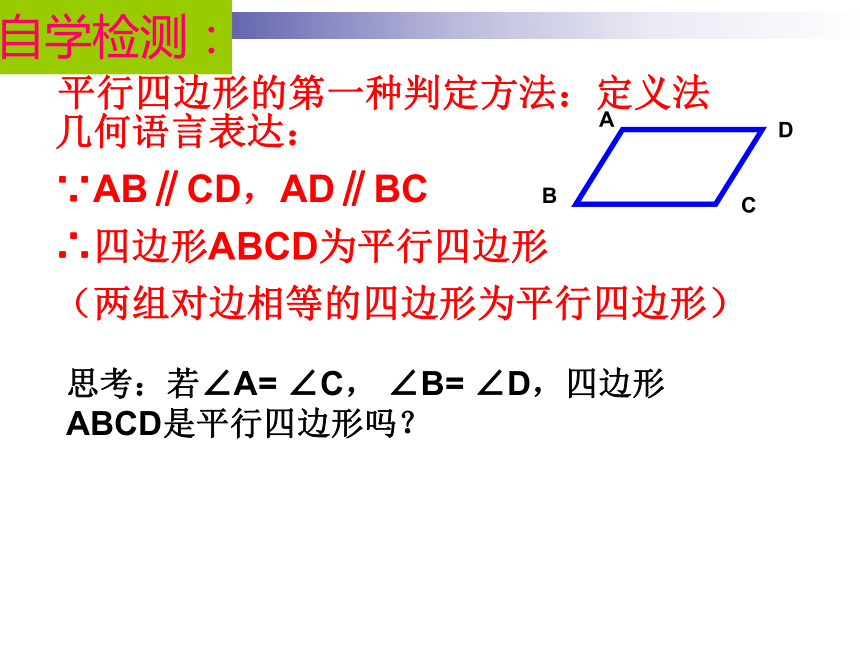
则四边形ABCD为平行四边形。自学检测:平行四边形的第一种判定方法:定义法几何语言表达:
∵AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
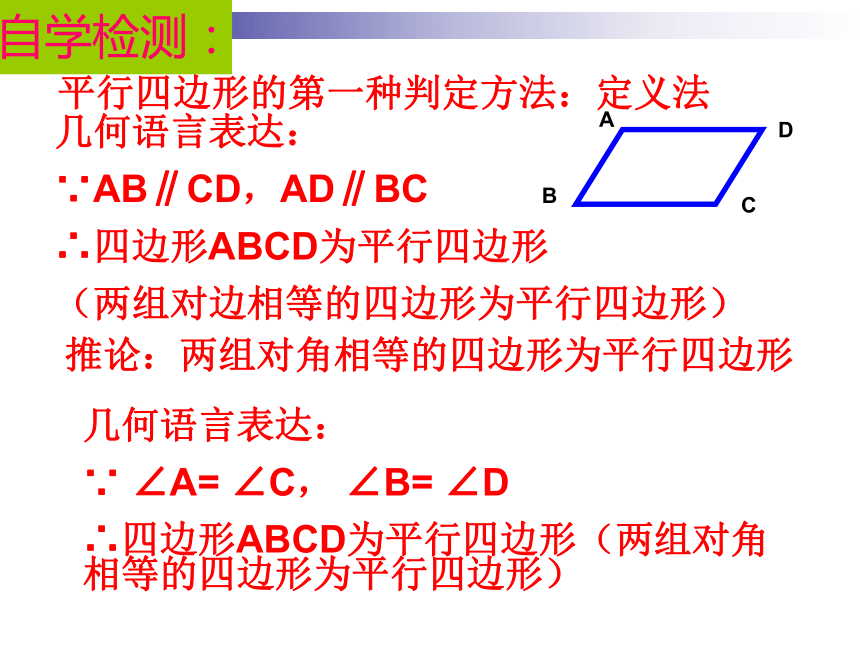
(两组对边相等的四边形为平行四边形)自学检测:思考:若∠A= ∠C, ∠B= ∠D,四边形ABCD是平行四边形吗?平行四边形的第一种判定方法:定义法几何语言表达:
∵AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
(两组对边相等的四边形为平行四边形)推论:两组对角相等的四边形为平行四边形几何语言表达:
∵ ∠A= ∠C, ∠B= ∠D
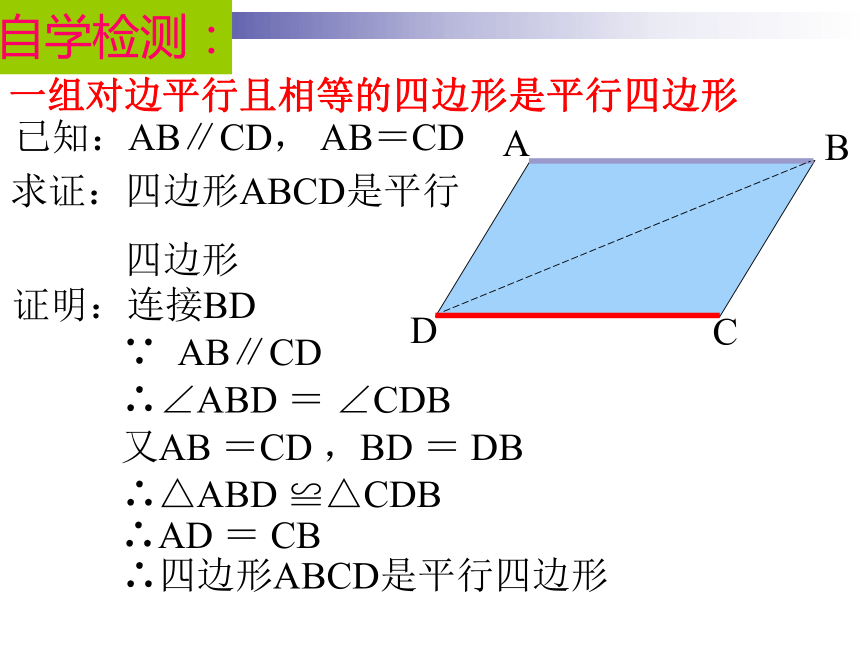
∴四边形ABCD为平行四边形(两组对角相等的四边形为平行四边形)自学检测:方法(二)D作AE∥BC,截取AD=BC,连接CD。自学检测:一组对边平行且相等的四边形是平行四边形已知:AB∥CD, AB=CD求证:四边形ABCD是平行
四边形证明:连接BD自学检测:平行四边形的第二种判定方法:几何语言表达:
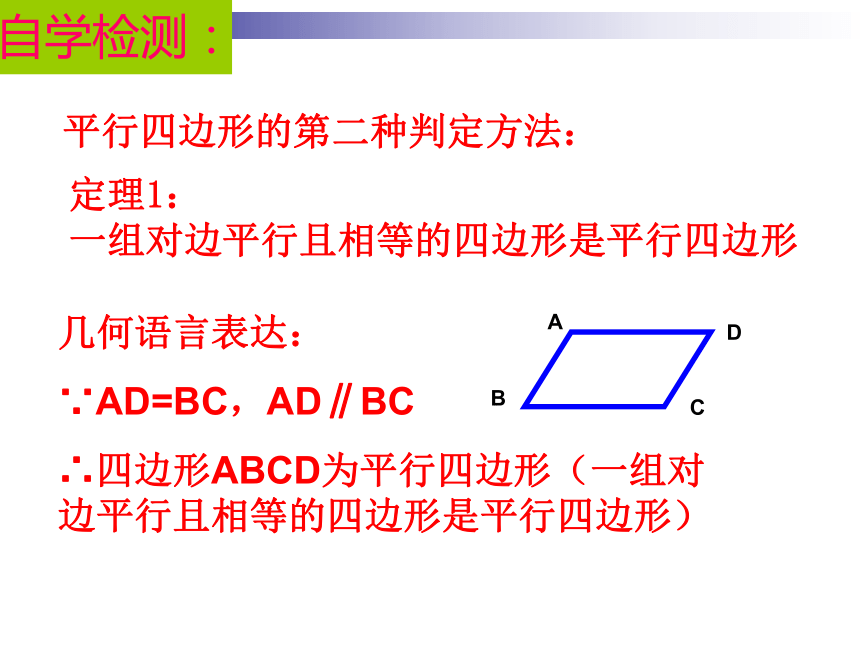
∵AD=BC,AD∥BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)定理1:
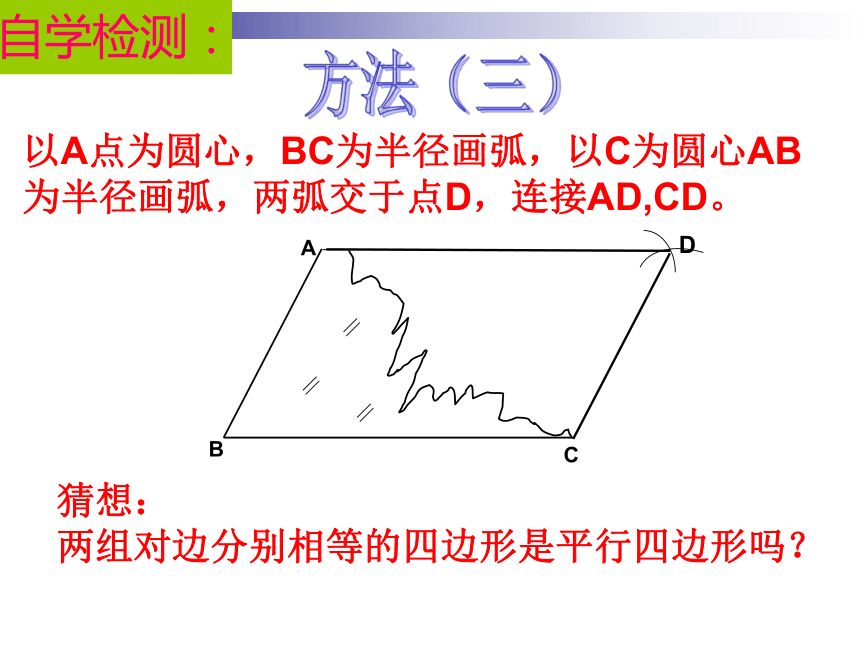
一组对边平行且相等的四边形是平行四边形自学检测:方法(三)D猜想:
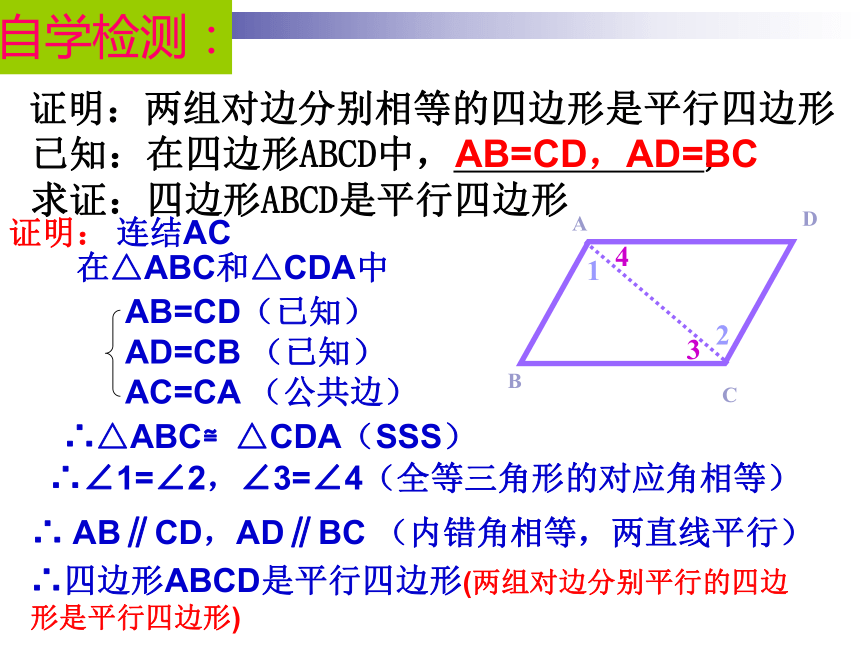
两组对边分别相等的四边形是平行四边形吗?以A点为圆心,BC为半径画弧,以C为圆心AB为半径画弧,两弧交于点D,连接AD,CD。自学检测:已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
证明:两组对边分别相等的四边形是平行四边形AB=CD,AD=BC自学检测:平行四边形的第三种判定方法:几何语言表达:
∵AB=CD,AD=BC
∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形)定理2:
两组对边分别相等的四边形是平行四边形自学检测:1、请你识别下列四边形哪些是平行四边形?为什么?⑴⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝基础练习: 2、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)基础练习:3.已知:如图,DC//EF//AB,DA//GH//CB,图中有多少平行四边形? 基础练习:4.已知:如图,平行四边形ABCD中,E、F分别是边AD和CB的中点.
求证:EF=AB基础练习:5.如图,AC=BD=16, AB=CD=EF=15, CE=DF=9. 图中有哪些互相平行的线段.ABDCEF基础练习:6. 如图,AC∥ED,点B在AC上且AB=ED=BC.请找出图中的平行四边形.ACBED基础练习:BDAC 7.已知:四边形ABCD, ∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
基础练习:8、已知:如图,CD是线段AB经平移所得的像,连结AD,BC.
求证:四边形ABCD是平行四边形。DCBA证明:∵CD是AB经平移所得的像,∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形)。基础练习:9.直角坐标系内有平行四边形的三个顶点,它们的坐标分别是A(2,1)、B(-1,-2)、C(3 , -2 ),试找出第四个顶点的位置,并写出它的坐标。基础练习:证明: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形
(两组对边平行且相等的四边形是平行四边形)在 AED和 CFB中同理可证:BE=DF 10.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形基础练习:11.已知:如图,AD⊥AC,BC⊥AC,
且AB=CD.求证:AB∥CD.CDAB基础练习:12.如图,在□ABCD中,BM垂直AC于M,DN垂直AC于N。 四边形BMDN是平行四边形吗?ABCDNM基础练习:13.已知:如图,?ABCD中,E、F、G、H分别是AB、BC、CD、AD上的点,且AE=CG,BF=DH. 求证:四边形EFGH是平行四边形. 基础练习:14.已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。基础练习:变形1:已知:平行四边形ABCD中,E、F分别
AD、BC上 的 点,AE=CF
求证:四边形BEDF是平行四边形
ABCDEF基础练习:变形2已知:ABCD中,E、F分别AD、BC 的
中点,G、H分别是AB、CD的中点,AH、
CG、BE、DF交点依次是M、 N、X、Y
求证:四边形MNXY是平行四边形.
ABCDEFGHMNXY本节课学习了什么内容?再见
2.理解定理1和定理2,并应用于平行四边形的判定中.自学内容:
课本77~79页
基础练习:平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD自学检测: 昨天初二的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战自学检测:方法(一)D根据平行四边形的定义:
作AE∥BC,CD∥AB,相交于D点,
则四边形ABCD为平行四边形。自学检测:平行四边形的第一种判定方法:定义法几何语言表达:
∵AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
(两组对边相等的四边形为平行四边形)自学检测:思考:若∠A= ∠C, ∠B= ∠D,四边形ABCD是平行四边形吗?平行四边形的第一种判定方法:定义法几何语言表达:
∵AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
(两组对边相等的四边形为平行四边形)推论:两组对角相等的四边形为平行四边形几何语言表达:
∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD为平行四边形(两组对角相等的四边形为平行四边形)自学检测:方法(二)D作AE∥BC,截取AD=BC,连接CD。自学检测:一组对边平行且相等的四边形是平行四边形已知:AB∥CD, AB=CD求证:四边形ABCD是平行
四边形证明:连接BD自学检测:平行四边形的第二种判定方法:几何语言表达:
∵AD=BC,AD∥BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)定理1:
一组对边平行且相等的四边形是平行四边形自学检测:方法(三)D猜想:
两组对边分别相等的四边形是平行四边形吗?以A点为圆心,BC为半径画弧,以C为圆心AB为半径画弧,两弧交于点D,连接AD,CD。自学检测:已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
证明:两组对边分别相等的四边形是平行四边形AB=CD,AD=BC自学检测:平行四边形的第三种判定方法:几何语言表达:
∵AB=CD,AD=BC
∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形)定理2:
两组对边分别相等的四边形是平行四边形自学检测:1、请你识别下列四边形哪些是平行四边形?为什么?⑴⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝基础练习: 2、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)基础练习:3.已知:如图,DC//EF//AB,DA//GH//CB,图中有多少平行四边形? 基础练习:4.已知:如图,平行四边形ABCD中,E、F分别是边AD和CB的中点.
求证:EF=AB基础练习:5.如图,AC=BD=16, AB=CD=EF=15, CE=DF=9. 图中有哪些互相平行的线段.ABDCEF基础练习:6. 如图,AC∥ED,点B在AC上且AB=ED=BC.请找出图中的平行四边形.ACBED基础练习:BDAC 7.已知:四边形ABCD, ∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
基础练习:8、已知:如图,CD是线段AB经平移所得的像,连结AD,BC.
求证:四边形ABCD是平行四边形。DCBA证明:∵CD是AB经平移所得的像,∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形)。基础练习:9.直角坐标系内有平行四边形的三个顶点,它们的坐标分别是A(2,1)、B(-1,-2)、C(3 , -2 ),试找出第四个顶点的位置,并写出它的坐标。基础练习:证明: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形
(两组对边平行且相等的四边形是平行四边形)在 AED和 CFB中同理可证:BE=DF 10.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形基础练习:11.已知:如图,AD⊥AC,BC⊥AC,
且AB=CD.求证:AB∥CD.CDAB基础练习:12.如图,在□ABCD中,BM垂直AC于M,DN垂直AC于N。 四边形BMDN是平行四边形吗?ABCDNM基础练习:13.已知:如图,?ABCD中,E、F、G、H分别是AB、BC、CD、AD上的点,且AE=CG,BF=DH. 求证:四边形EFGH是平行四边形. 基础练习:14.已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。基础练习:变形1:已知:平行四边形ABCD中,E、F分别
AD、BC上 的 点,AE=CF
求证:四边形BEDF是平行四边形
ABCDEF基础练习:变形2已知:ABCD中,E、F分别AD、BC 的
中点,G、H分别是AB、CD的中点,AH、
CG、BE、DF交点依次是M、 N、X、Y
求证:四边形MNXY是平行四边形.
ABCDEFGHMNXY本节课学习了什么内容?再见
