沪科版八年级数学上册12.3.1一次函数与二元一次方程组教学设计(表格式)
文档属性
| 名称 | 沪科版八年级数学上册12.3.1一次函数与二元一次方程组教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 118.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

文档简介
12.3.1一次函数与二元一次方程组
教学目标 知识与 技能 掌握一次函数与二元一次方程组的对应关系; 会用画图像的方法解二元一次方程组。
过程与 方法 通过对一次函数与二元一次方程组关系的探究及相关实际问题的解决,学会用函数的观点去认识问题的方法。
情感、态度与价值观 1、通过对一次函数与二元一次方程组关系的探索,培养学生严谨的科学态度及用于探索的精神; 2、通过从函数的角度看问题,让学生体会数学的价值。
教学重点 探索一次函数与二元一次方程组关系。
教学难点 综合运用一次函数与二元一次方程组关系解决实际问题。
教学方法 自主 、交流、展示
课时说明 第一课时:14.3.1一次函数与二元一次方程组 第二课时:练习巩固
教学流程 内 容 学法 指导
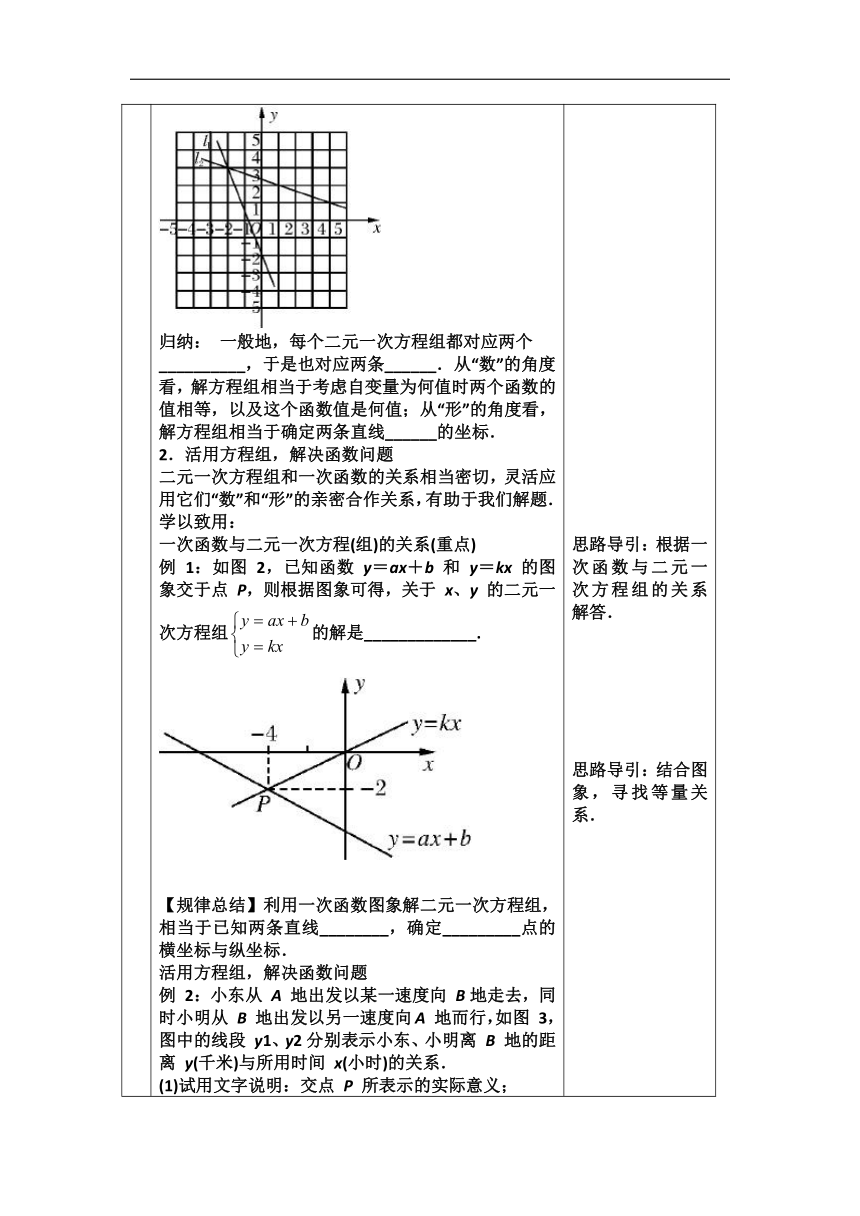
自主学习 温故知新:一次函数:________________________; 一般形式:___________________________________. 二元一次方程组:_________________________; 一般形式:___________________________________. 1.一次函数与二元一次方程(组)的关系 探究:如图 1,在同一平面直角坐标系中作出一次函数 y1、y2的图象 l1、l2,设 y1=k1x+b1,y2=k2x+b2,则两条直线的交点坐标为_________. 方程组的解是 归纳: 一般地,每个二元一次方程组都对应两个 __________,于是也对应两条______.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线______的坐标. 2.活用方程组,解决函数问题 二元一次方程组和一次函数的关系相当密切,灵活应用它们“数”和“形”的亲密合作关系,有助于我们解题. 学以致用: 一次函数与二元一次方程(组)的关系(重点) 例 1:如图 2,已知函数 y=ax+b 和 y=kx 的图象交于点 P,则根据图象可得,关于 x、y 的二元一次方程组的解是_____________. 【规律总结】利用一次函数图象解二元一次方程组,相当于已知两条直线________,确定_________点的横坐标与纵坐标. 活用方程组,解决函数问题 例 2:小东从 A 地出发以某一速度向 B地走去,同时小明从 B 地出发以另一速度向A 地而行,如图 3,图中的线段 y1、y2分别表示小东、小明离 B 地的距离 y(千米)与所用时间 x(小时)的关系. (1)试用文字说明:交点 P 所表示的实际意义; (2)试求出 A、B 两地之间的距离. 思路导引:根据一次函数与二元一次方程组的关系解答. 思路导引:结合图象,寻找等量关系.
自主学习 温故知新:一次函数:________________________; 一般形式:___________________________________. 二元一次方程组:_________________________; 一般形式:___________________________________. 1.一次函数与二元一次方程(组)的关系 探究:如图 1,在同一平面直角坐标系中作出一次函数 y1、y2的图象 l1、l2,设 y1=k1x+b1,y2=k2x+b2,则两条直线的交点坐标为_________. 方程组的解是 归纳: 一般地,每个二元一次方程组都对应两个 __________,于是也对应两条______.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线______的坐标. 2.活用方程组,解决函数问题 二元一次方程组和一次函数的关系相当密切,灵活应用它们“数”和“形”的亲密合作关系,有助于我们解题. 学以致用: 一次函数与二元一次方程(组)的关系(重点) 例 1:如图 2,已知函数 y=ax+b 和 y=kx 的图象交于点 P,则根据图象可得,关于 x、y 的二元一次方程组的解是_____________. 【规律总结】利用一次函数图象解二元一次方程组,相当于已知两条直线________,确定_________点的横坐标与纵坐标. 活用方程组,解决函数问题 例 2:小东从 A 地出发以某一速度向 B地走去,同时小明从 B 地出发以另一速度向A 地而行,如图 3,图中的线段 y1、y2分别表示小东、小明离 B 地的距离 y(千米)与所用时间 x(小时)的关系. (1)试用文字说明:交点 P 所表示的实际意义; (2)试求出 A、B 两地之间的距离. 思路导引:根据一次函数与二元一次方程组的关系解答. 思路导引:结合图象,寻找等量关系.
交流 展示 教师分配展示任务,各小组派代表分组展示。 各组组员认真检查,评价。
反馈提高 1.已知二元一次方程 x+y=3 与 3x-y=5 有一组公共解,那么一次函数 y=3-x 与 y=3x-5 的图象的交点坐标为( ) A.(1,2) B.(2,1) C.(-1,2) D.(-2,1) 2.小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1、l2如图 4,他解的这个方程组是( ) 请将习题答案完成在此处
板书设计 14.3.1一次函数与二元一次方程组
教学反思
教学目标 知识与 技能 掌握一次函数与二元一次方程组的对应关系; 会用画图像的方法解二元一次方程组。
过程与 方法 通过对一次函数与二元一次方程组关系的探究及相关实际问题的解决,学会用函数的观点去认识问题的方法。
情感、态度与价值观 1、通过对一次函数与二元一次方程组关系的探索,培养学生严谨的科学态度及用于探索的精神; 2、通过从函数的角度看问题,让学生体会数学的价值。
教学重点 探索一次函数与二元一次方程组关系。
教学难点 综合运用一次函数与二元一次方程组关系解决实际问题。
教学方法 自主 、交流、展示
课时说明 第一课时:14.3.1一次函数与二元一次方程组 第二课时:练习巩固
教学流程 内 容 学法 指导
自主学习 温故知新:一次函数:________________________; 一般形式:___________________________________. 二元一次方程组:_________________________; 一般形式:___________________________________. 1.一次函数与二元一次方程(组)的关系 探究:如图 1,在同一平面直角坐标系中作出一次函数 y1、y2的图象 l1、l2,设 y1=k1x+b1,y2=k2x+b2,则两条直线的交点坐标为_________. 方程组的解是 归纳: 一般地,每个二元一次方程组都对应两个 __________,于是也对应两条______.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线______的坐标. 2.活用方程组,解决函数问题 二元一次方程组和一次函数的关系相当密切,灵活应用它们“数”和“形”的亲密合作关系,有助于我们解题. 学以致用: 一次函数与二元一次方程(组)的关系(重点) 例 1:如图 2,已知函数 y=ax+b 和 y=kx 的图象交于点 P,则根据图象可得,关于 x、y 的二元一次方程组的解是_____________. 【规律总结】利用一次函数图象解二元一次方程组,相当于已知两条直线________,确定_________点的横坐标与纵坐标. 活用方程组,解决函数问题 例 2:小东从 A 地出发以某一速度向 B地走去,同时小明从 B 地出发以另一速度向A 地而行,如图 3,图中的线段 y1、y2分别表示小东、小明离 B 地的距离 y(千米)与所用时间 x(小时)的关系. (1)试用文字说明:交点 P 所表示的实际意义; (2)试求出 A、B 两地之间的距离. 思路导引:根据一次函数与二元一次方程组的关系解答. 思路导引:结合图象,寻找等量关系.
自主学习 温故知新:一次函数:________________________; 一般形式:___________________________________. 二元一次方程组:_________________________; 一般形式:___________________________________. 1.一次函数与二元一次方程(组)的关系 探究:如图 1,在同一平面直角坐标系中作出一次函数 y1、y2的图象 l1、l2,设 y1=k1x+b1,y2=k2x+b2,则两条直线的交点坐标为_________. 方程组的解是 归纳: 一般地,每个二元一次方程组都对应两个 __________,于是也对应两条______.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线______的坐标. 2.活用方程组,解决函数问题 二元一次方程组和一次函数的关系相当密切,灵活应用它们“数”和“形”的亲密合作关系,有助于我们解题. 学以致用: 一次函数与二元一次方程(组)的关系(重点) 例 1:如图 2,已知函数 y=ax+b 和 y=kx 的图象交于点 P,则根据图象可得,关于 x、y 的二元一次方程组的解是_____________. 【规律总结】利用一次函数图象解二元一次方程组,相当于已知两条直线________,确定_________点的横坐标与纵坐标. 活用方程组,解决函数问题 例 2:小东从 A 地出发以某一速度向 B地走去,同时小明从 B 地出发以另一速度向A 地而行,如图 3,图中的线段 y1、y2分别表示小东、小明离 B 地的距离 y(千米)与所用时间 x(小时)的关系. (1)试用文字说明:交点 P 所表示的实际意义; (2)试求出 A、B 两地之间的距离. 思路导引:根据一次函数与二元一次方程组的关系解答. 思路导引:结合图象,寻找等量关系.
交流 展示 教师分配展示任务,各小组派代表分组展示。 各组组员认真检查,评价。
反馈提高 1.已知二元一次方程 x+y=3 与 3x-y=5 有一组公共解,那么一次函数 y=3-x 与 y=3x-5 的图象的交点坐标为( ) A.(1,2) B.(2,1) C.(-1,2) D.(-2,1) 2.小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1、l2如图 4,他解的这个方程组是( ) 请将习题答案完成在此处
板书设计 14.3.1一次函数与二元一次方程组
教学反思
