18.1 勾股定理(1)学案
文档属性
| 名称 | 18.1 勾股定理(1)学案 |  | |
| 格式 | zip | ||
| 文件大小 | 135.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-20 22:33:55 | ||
图片预览

文档简介
学科:数学 年级:八年级 主备人: 审核人: 课题:勾股定理 (1) 课型:预习+展示 小主人姓名:
*学习目标*:1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。2.培养在实际生活中发现问题总结规律的意识和能力。了解我国古代在勾股定理研究方面所取得的成就。 3.经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。*学习重点*:股定理的内容及证明。*学习难点*:勾股定理的证明。
学习过程 学法指导
一。*知识回顾*1.直角三角形的性质:(1)直角三角形两锐角 ;(2)直角三角形斜边上的中线等于 ;(3)直角三角形中30°的角所对的直角边等于 。2.分别求出下式中的x的值:①x2=5 ②(x-2)2=5 ③2(2x-1)2=9二.*能力生成*1、2002年北京召开了被誉为数学界“奥运会”的国际数学家大会,这就是当时采用的会徽. 2、相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系.
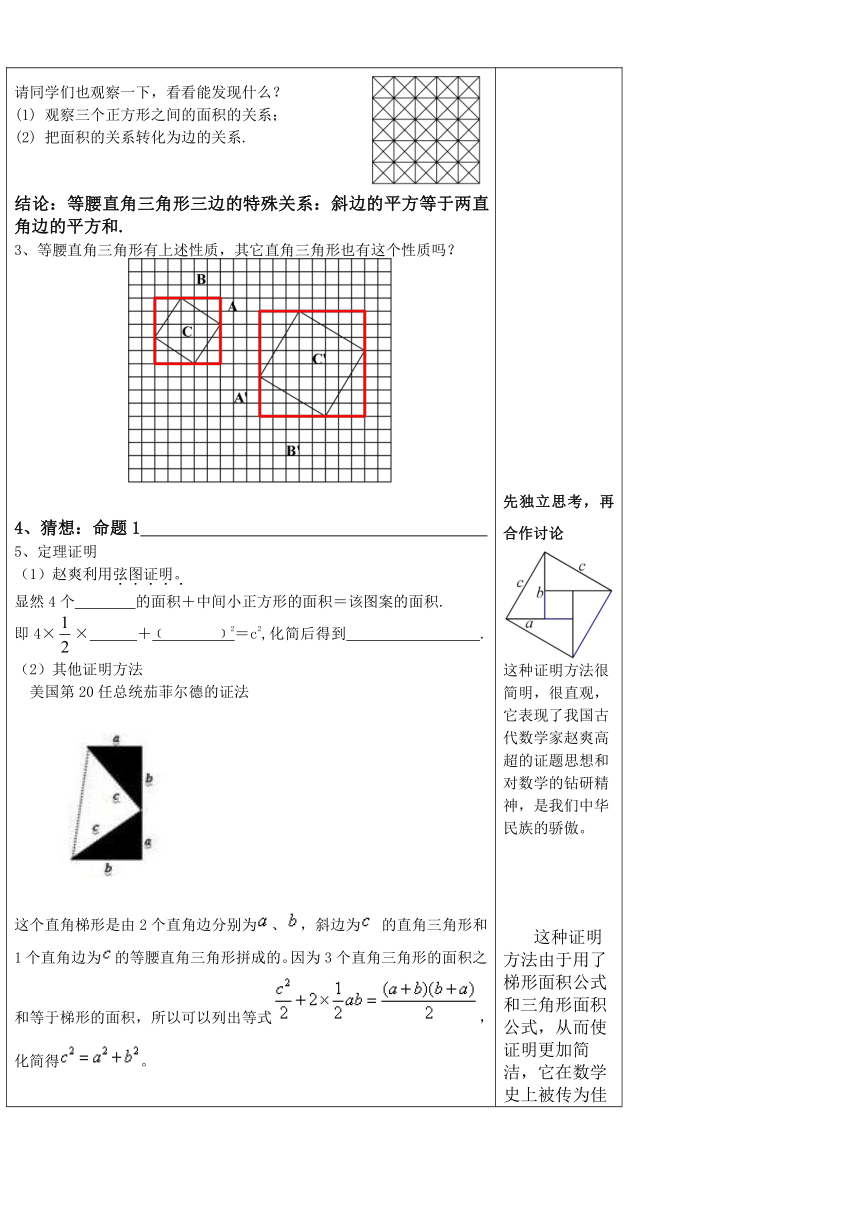
请同学们也观察一下,看看能发现什么?(1) 观察三个正方形之间的面积的关系;(2) 把面积的关系转化为边的关系.结论:等腰直角三角形三边的特殊关系:斜边的平方等于两直角边的平方和.3、等腰直角三角形有上述性质,其它直角三角形也有这个性质吗?4、猜想:命题1 5、定理证明(1)赵爽利用弦图证明。显然4个 的面积+中间小正方形的面积=该图案的面积.即4×× +﹝ ﹞2=c2,化简后得到 .(2)其他证明方法美国第20任总统茄菲尔德的证法 这个直角梯形是由2个直角边分别为、,斜边为 的直角三角形和1个直角边为的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。6.由 得:c= a= b= 三.*巩固提升*1、在Rt△ABC中,∠C=,AB=17,BC=8,求AC的长2、Rt△ABC和以AB为边的正方形ABEF,∠ACB=90°,AC=12,BC=5,则正方形的面积是______.3、四.*检测反馈* 1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )A.斜边长为25 B.三角形的周长为25 C.斜边长为5 D.三角形面积为202.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,则斜边长为( )A.4 B.8 C.10 D.123.直角三角形的两直角边的长分别是5和12,则其斜边上的高的长为( )A.6 B.8 C. D.★★4、已知,如图1-1-5,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求CF CE 先独立思考,再合作讨论这种证明方法很简明,很直观,它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神,是我们中华民族的骄傲。这种证明方法由于用了梯形面积公式和三角形面积公式,从而使证明更加简洁,它在数学史上被传为佳话。即学即练一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
图1-1-5
*学习目标*:1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。2.培养在实际生活中发现问题总结规律的意识和能力。了解我国古代在勾股定理研究方面所取得的成就。 3.经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。*学习重点*:股定理的内容及证明。*学习难点*:勾股定理的证明。
学习过程 学法指导
一。*知识回顾*1.直角三角形的性质:(1)直角三角形两锐角 ;(2)直角三角形斜边上的中线等于 ;(3)直角三角形中30°的角所对的直角边等于 。2.分别求出下式中的x的值:①x2=5 ②(x-2)2=5 ③2(2x-1)2=9二.*能力生成*1、2002年北京召开了被誉为数学界“奥运会”的国际数学家大会,这就是当时采用的会徽. 2、相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系.
请同学们也观察一下,看看能发现什么?(1) 观察三个正方形之间的面积的关系;(2) 把面积的关系转化为边的关系.结论:等腰直角三角形三边的特殊关系:斜边的平方等于两直角边的平方和.3、等腰直角三角形有上述性质,其它直角三角形也有这个性质吗?4、猜想:命题1 5、定理证明(1)赵爽利用弦图证明。显然4个 的面积+中间小正方形的面积=该图案的面积.即4×× +﹝ ﹞2=c2,化简后得到 .(2)其他证明方法美国第20任总统茄菲尔德的证法 这个直角梯形是由2个直角边分别为、,斜边为 的直角三角形和1个直角边为的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。6.由 得:c= a= b= 三.*巩固提升*1、在Rt△ABC中,∠C=,AB=17,BC=8,求AC的长2、Rt△ABC和以AB为边的正方形ABEF,∠ACB=90°,AC=12,BC=5,则正方形的面积是______.3、四.*检测反馈* 1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )A.斜边长为25 B.三角形的周长为25 C.斜边长为5 D.三角形面积为202.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,则斜边长为( )A.4 B.8 C.10 D.123.直角三角形的两直角边的长分别是5和12,则其斜边上的高的长为( )A.6 B.8 C. D.★★4、已知,如图1-1-5,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求CF CE 先独立思考,再合作讨论这种证明方法很简明,很直观,它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神,是我们中华民族的骄傲。这种证明方法由于用了梯形面积公式和三角形面积公式,从而使证明更加简洁,它在数学史上被传为佳话。即学即练一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
图1-1-5
