18.1 勾股定理(2)学案
文档属性
| 名称 | 18.1 勾股定理(2)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-20 00:00:00 | ||
图片预览

文档简介
学科:八年级数学 主备人: 审核人: 课题:勾股定理(2) 课型:预习+展示 小主人姓名:
*学习目标*:1.通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。2、利用勾股定理,能在数轴上表示无理数的点*学习重点*:勾股定理的应用,会在数轴上表示(n为正整数)*学习难点*:实际问题向数学问题的转化。
学习过程 学法指导
一。*知识回顾*1.勾股定理的内容: 2.几组常用的勾股数为:二.*能力生成*活动一 1、一个门框的尺寸如图所示: (1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?分析:(3) 木板的宽2.2米大于1米,所以横着不能从门框内通过.木板的宽2.2米大于2米,所以竖着不能从门框内通过.因为对角线AC的长度最大,所以只能试试斜着能否通过.所以将实际问题转化为数学问题.
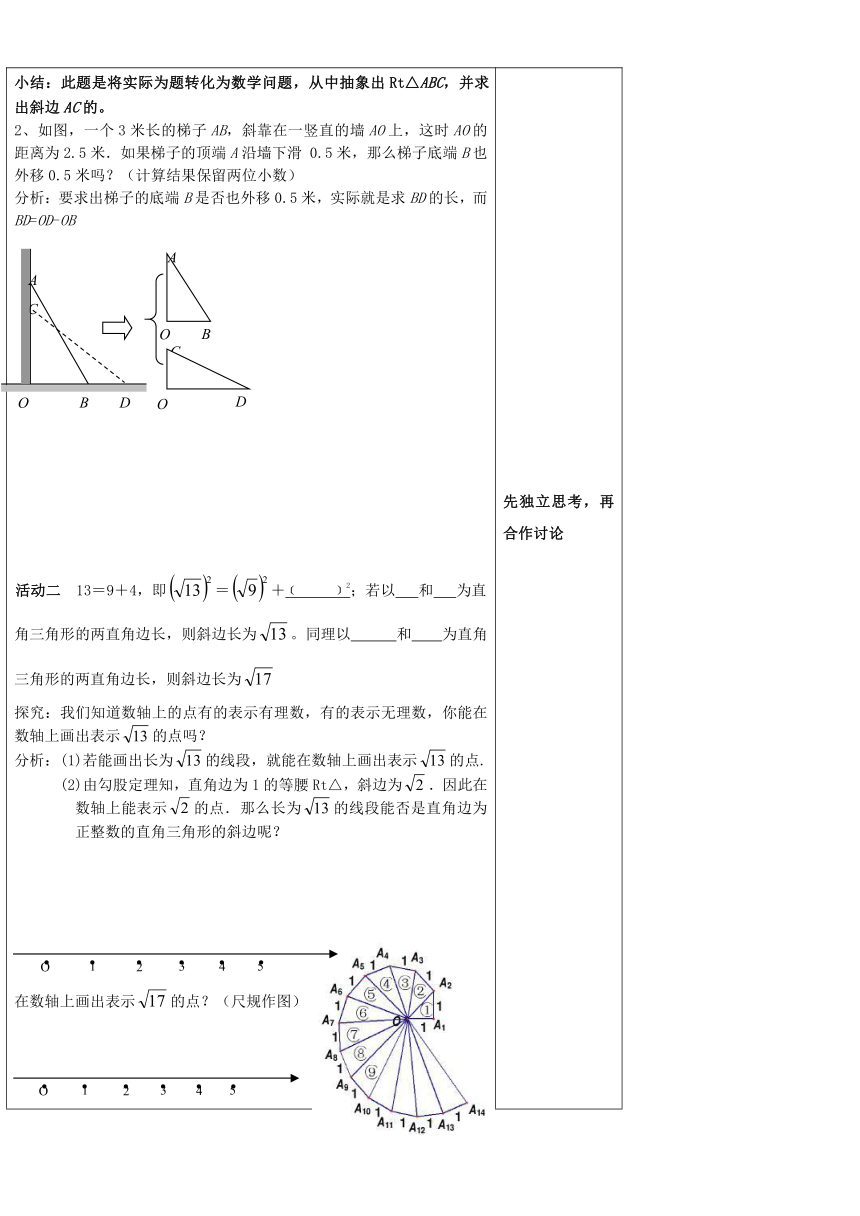
小结:此题是将实际为题转化为数学问题,从中抽象出Rt△ABC,并求出斜边AC的。2、如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米.如果梯子的顶端A沿墙下滑 0.5米,那么梯子底端B也外移0.5米吗?(计算结果保留两位小数)分析:要求出梯子的底端B是否也外移0.5米,实际就是求BD的长,而BD=OD-OB活动二 13=9+4,即=+﹝ ﹞2;若以 和 为直角三角形的两直角边长,则斜边长为。同理以 和 为直角三角形的两直角边长,则斜边长为探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?分析:(1)若能画出长为的线段,就能在数轴上画出表示的点. (2)由勾股定理知,直角边为1的等腰Rt△,斜边为.因此在数轴上能表示的点.那么长为的线段能否是直角边为正整数的直角三角形的斜边呢?在数轴上画出表示的点?(尺规作图)2、如图:螺旋状图形是由若干个直角三角形所组成的,其中①是直角边长为1的等腰直角三角形。那么OA1= ,OA2= ,OA3= ,OA4= ,OA5= ,OA6= ,OA7= ,…,OA14 = , …,OAn= .思考:怎样在数轴上画出表示(n为正整数)的点?三.*巩固提升*1、已知正三角形ABC的边长为a,求△ABC的面积?2、在数轴上找出表示的点。3.小明拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖着来拿,结果竹竿比城门高1米,当他把竹竿斜着时,竹竿的两端刚好顶着城门的对角,问竹竿长多少米?四.*检测反馈*1、一圆柱底面周长为6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,求爬行的最短距离。 2、将一个长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度是hcm,求h的范围。3、有一根70cm长的木棒,要放在长、宽、高分别是50cm,40cm,30cm的木箱中,能否放进去? 先独立思考,再合作讨论即学即练一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
O
B
D
CC
A
C
A
O
B
O
D
5
●
●
●
●
●
●
O
1
2
3
4
5
●
●
●
●
●
●
O
1
2
3
4
5
●
●
●
●
●
●
O
1
2
3
4
*学习目标*:1.通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。2、利用勾股定理,能在数轴上表示无理数的点*学习重点*:勾股定理的应用,会在数轴上表示(n为正整数)*学习难点*:实际问题向数学问题的转化。
学习过程 学法指导
一。*知识回顾*1.勾股定理的内容: 2.几组常用的勾股数为:二.*能力生成*活动一 1、一个门框的尺寸如图所示: (1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?分析:(3) 木板的宽2.2米大于1米,所以横着不能从门框内通过.木板的宽2.2米大于2米,所以竖着不能从门框内通过.因为对角线AC的长度最大,所以只能试试斜着能否通过.所以将实际问题转化为数学问题.
小结:此题是将实际为题转化为数学问题,从中抽象出Rt△ABC,并求出斜边AC的。2、如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米.如果梯子的顶端A沿墙下滑 0.5米,那么梯子底端B也外移0.5米吗?(计算结果保留两位小数)分析:要求出梯子的底端B是否也外移0.5米,实际就是求BD的长,而BD=OD-OB活动二 13=9+4,即=+﹝ ﹞2;若以 和 为直角三角形的两直角边长,则斜边长为。同理以 和 为直角三角形的两直角边长,则斜边长为探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?分析:(1)若能画出长为的线段,就能在数轴上画出表示的点. (2)由勾股定理知,直角边为1的等腰Rt△,斜边为.因此在数轴上能表示的点.那么长为的线段能否是直角边为正整数的直角三角形的斜边呢?在数轴上画出表示的点?(尺规作图)2、如图:螺旋状图形是由若干个直角三角形所组成的,其中①是直角边长为1的等腰直角三角形。那么OA1= ,OA2= ,OA3= ,OA4= ,OA5= ,OA6= ,OA7= ,…,OA14 = , …,OAn= .思考:怎样在数轴上画出表示(n为正整数)的点?三.*巩固提升*1、已知正三角形ABC的边长为a,求△ABC的面积?2、在数轴上找出表示的点。3.小明拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖着来拿,结果竹竿比城门高1米,当他把竹竿斜着时,竹竿的两端刚好顶着城门的对角,问竹竿长多少米?四.*检测反馈*1、一圆柱底面周长为6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,求爬行的最短距离。 2、将一个长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度是hcm,求h的范围。3、有一根70cm长的木棒,要放在长、宽、高分别是50cm,40cm,30cm的木箱中,能否放进去? 先独立思考,再合作讨论即学即练一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
O
B
D
CC
A
C
A
O
B
O
D
5
●
●
●
●
●
●
O
1
2
3
4
5
●
●
●
●
●
●
O
1
2
3
4
5
●
●
●
●
●
●
O
1
2
3
4
