18.2 勾股定理的逆定理(2)学案
文档属性
| 名称 | 18.2 勾股定理的逆定理(2)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 122.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-20 22:36:38 | ||
图片预览

文档简介
课题:勾股定理的逆定理(2) 课型:预习+展示主备人: 审核人: 小主人姓名:
*学习目标*:1、进一步掌握勾股定理的逆定理,并能运用勾股定理的逆定理解决有关问题。2、在探究活动过程中,经历知识的发生、发展与形成的过程. 培养敢于实践、勇于发现、大胆探索、合作创新的精神,增强学好数学、用好数学的信心和勇气.*学习重点*:勾股定理的逆定理及其实际应用.*学习难点*:勾股定理逆定理的灵活应用.
学习过程 学法指导
一。*知识回顾*1、勾股定理是直角三角形的 定理;它的逆定理是直角三角形的 定理.2、请写出三组不同的勾股数: 、 、 .3、测得一块三角形麦田三边长分别为9m,12m,15m,则这块麦田的面积为________㎡。二.*能力生成* 借助三角板画出如下方位角所确定的射线:①南偏东30°;②西南方向;③北偏西60°. 1、上北下南左西右东2、南偏东30°即以正南为起始线逆时针旋转30°3、西南方向即南偏西45°。
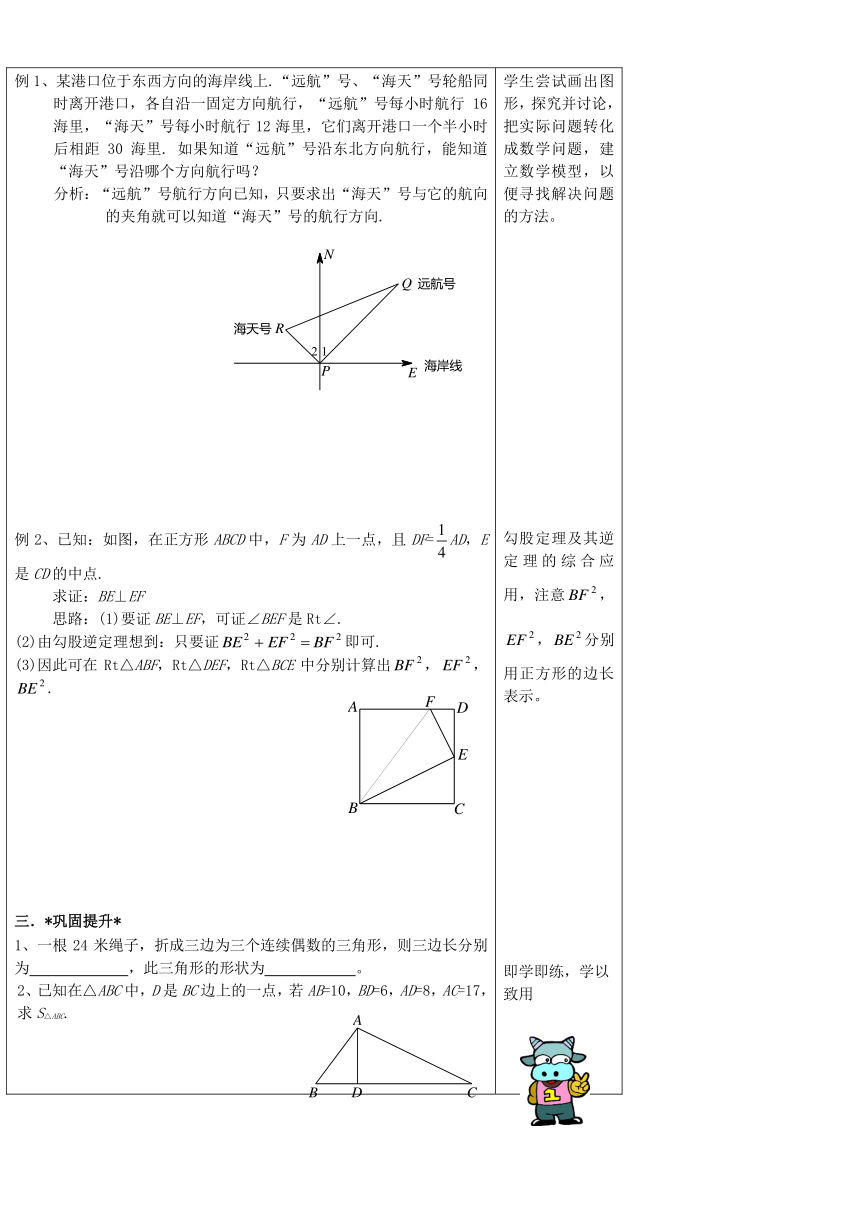
例1、某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里. 如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?分析:“远航”号航行方向已知,只要求出“海天”号与它的航向的夹角就可以知道“海天”号的航行方向.例2、已知:如图,在正方形ABCD中,F为AD上一点,且DF=AD,E是CD的中点.求证:BE⊥EF思路:(1)要证BE⊥EF,可证∠BEF是Rt∠.(2)由勾股逆定理想到:只要证即可.(3)因此可在Rt△ABF,Rt△DEF,Rt△BCE中分别计算出,,.三.*巩固提升*1、一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 。2、已知在△ABC中,D是BC边上的一点,若AB=10,BD=6,AD=8,AC=17,求S△ABC.3、已知,则以x、y、z为三边的三角形是什么形状的三角形?四.*检测反馈*如图所示,是一个零件的形状,按规定这个零件中的AD与CD必须互相垂直,工人师傅通过测量得到A到C的距离是10cm,AD=8cm,CD=6cm,问这个零件是否合格?五 *扩展迁移*如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。 学生尝试画出图形,探究并讨论,把实际问题转化成数学问题,建立数学模型,以便寻找解决问题的方法。勾股定理及其逆定理的综合应用,注意,,分别用正方形的边长表示。即学即练,学以致用此题要判断三角形的形状,我们要知道x、y、z的长度,然后根据勾股定理的逆定理判断三角形的形状。利用数学知识解决实际问题,体现数学与日常生活的紧密联系,进一步体现学习数学的重要性,激发学生的学习兴趣。勾股定理及其逆定理中的动点问题,分析时应分两种情况讨论,即PA⊥AC和PA⊥AB。一分耕耘一分收获,你的收获有多大!
①
②
③
注意双色笔的使用哦!
*学习目标*:1、进一步掌握勾股定理的逆定理,并能运用勾股定理的逆定理解决有关问题。2、在探究活动过程中,经历知识的发生、发展与形成的过程. 培养敢于实践、勇于发现、大胆探索、合作创新的精神,增强学好数学、用好数学的信心和勇气.*学习重点*:勾股定理的逆定理及其实际应用.*学习难点*:勾股定理逆定理的灵活应用.
学习过程 学法指导
一。*知识回顾*1、勾股定理是直角三角形的 定理;它的逆定理是直角三角形的 定理.2、请写出三组不同的勾股数: 、 、 .3、测得一块三角形麦田三边长分别为9m,12m,15m,则这块麦田的面积为________㎡。二.*能力生成* 借助三角板画出如下方位角所确定的射线:①南偏东30°;②西南方向;③北偏西60°. 1、上北下南左西右东2、南偏东30°即以正南为起始线逆时针旋转30°3、西南方向即南偏西45°。
例1、某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里. 如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?分析:“远航”号航行方向已知,只要求出“海天”号与它的航向的夹角就可以知道“海天”号的航行方向.例2、已知:如图,在正方形ABCD中,F为AD上一点,且DF=AD,E是CD的中点.求证:BE⊥EF思路:(1)要证BE⊥EF,可证∠BEF是Rt∠.(2)由勾股逆定理想到:只要证即可.(3)因此可在Rt△ABF,Rt△DEF,Rt△BCE中分别计算出,,.三.*巩固提升*1、一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 。2、已知在△ABC中,D是BC边上的一点,若AB=10,BD=6,AD=8,AC=17,求S△ABC.3、已知,则以x、y、z为三边的三角形是什么形状的三角形?四.*检测反馈*如图所示,是一个零件的形状,按规定这个零件中的AD与CD必须互相垂直,工人师傅通过测量得到A到C的距离是10cm,AD=8cm,CD=6cm,问这个零件是否合格?五 *扩展迁移*如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。 学生尝试画出图形,探究并讨论,把实际问题转化成数学问题,建立数学模型,以便寻找解决问题的方法。勾股定理及其逆定理的综合应用,注意,,分别用正方形的边长表示。即学即练,学以致用此题要判断三角形的形状,我们要知道x、y、z的长度,然后根据勾股定理的逆定理判断三角形的形状。利用数学知识解决实际问题,体现数学与日常生活的紧密联系,进一步体现学习数学的重要性,激发学生的学习兴趣。勾股定理及其逆定理中的动点问题,分析时应分两种情况讨论,即PA⊥AC和PA⊥AB。一分耕耘一分收获,你的收获有多大!
①
②
③
注意双色笔的使用哦!
