北京版2020-2021学年北京市丰台区五年级下期末数学试卷(word版含答案)
文档属性
| 名称 | 北京版2020-2021学年北京市丰台区五年级下期末数学试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 331.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览



文档简介
2020-2021学年北京市丰台区五年级(下)期末数学试卷
一、选择正确答案,将选项涂在答题纸上(每题只有一个正确答案)。
1.在下面每组数中,有因数和倍数关系的是( )
A.3和24 B.1.8和6 C.2和7 D.12和5
2.在10到40中,7的倍数共有( )个。
A.3 B.4 C.5 D.6
3.两个不同质数的乘积一共有( )个因数。
A.1 B.2 C.3 D.4
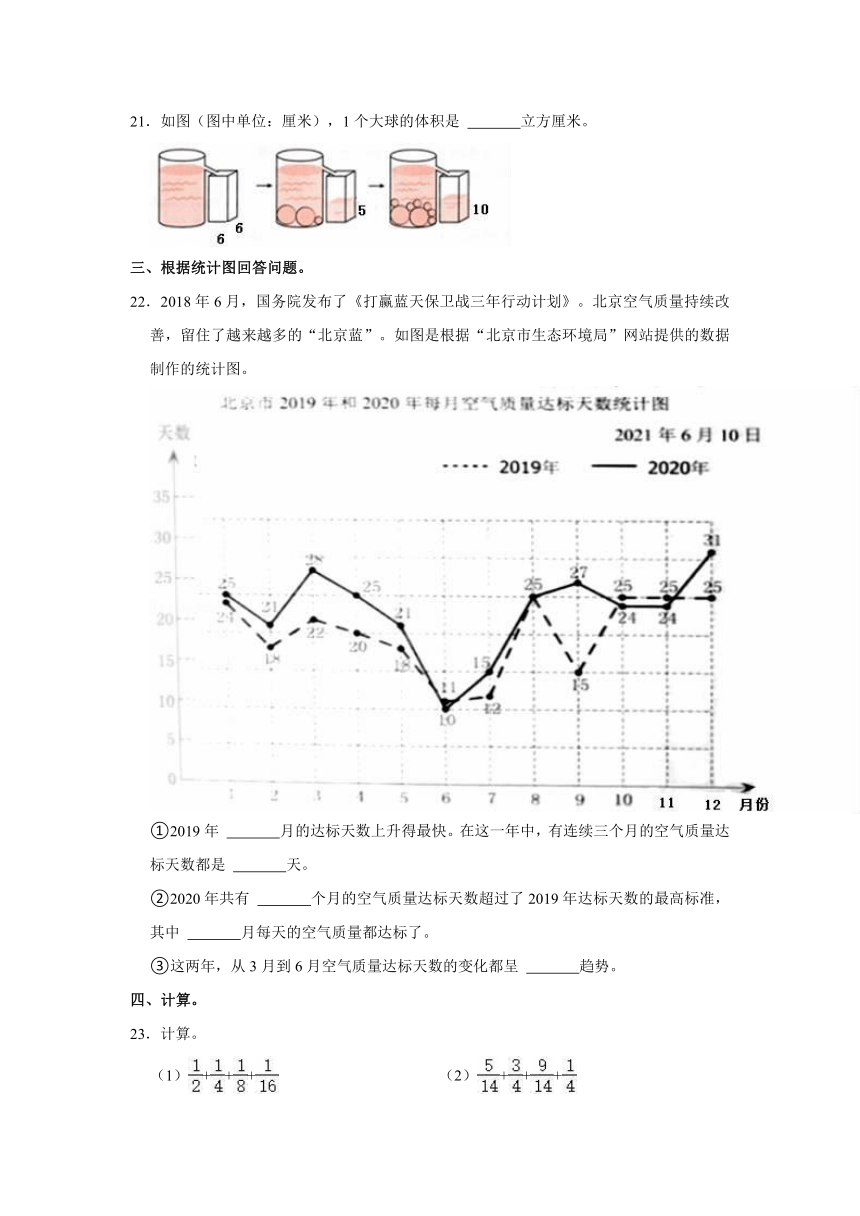
4.在“403□”的方框里填个数,使这个四位数既是5的倍数,又有因数3,方框里应该填( )
A.0 B.2 C.5 D.8
5.a为正整数,则a和a+1的最小公倍数是它们最大公因数的( )倍。
A.1 B.a C.a+1 D.a (a+1)
6.把你的拳头伸进盛满水的盆中,溢出来的水的体积( )
A.小于10毫升 B.小于1升 C.等于1升 D.大于1升
7.如果a+=b+=c+=d+,那么在a、b、c、d中,最大的数是( )
A.a B.b C.c D.d
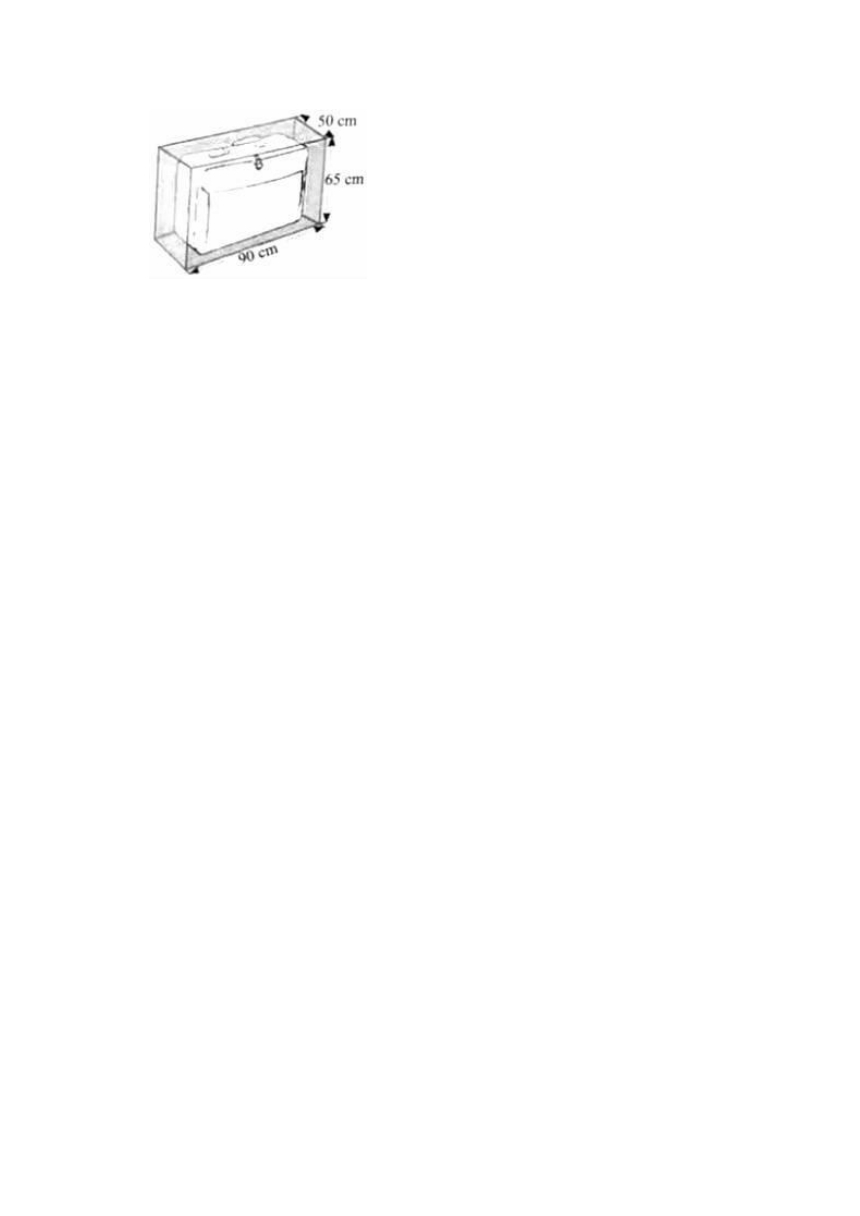
8.是假分数,也是假分数。如果a表示同一个数,那么这两个分数的和一定( )
A.小于2 B.等于2 C.大于2 D.不小于2
9.如图中N点表示的数是( )
A. B. C. D.
10.一块木板截去了平方分米,还剩下这块木板的。下面说法正确的是( )
A.两部分同样大 B.截去的部分大
C.剩下的部分大 D.剩下平方分米
11.下面的折纸材料中,沿着虚线不能折成长方体或正方体的是图( )
A. B.
C. D.
12.在模型A的基础上添加一个小正方体后得到模型B、C、D,模型B、C、D中,( )的表面积最小。
A. B. C. D.
二、填空。
13.750mL= cm3
15分=时
14.0.6= ÷ =
15.把棱长1分米的正方体木块分成棱长是1厘米的小正方体木块后,再把这些小正方体木块摆成一排,成为一个长方体。这个长方体的表面积是 平方厘米。
16.在、中,能化成有限小数的是 ,化成的有限小数是 。
17.把九个完全相同的球,先按照1~9编号,然后放进盒子里。小红和小明玩摸球游戏,规定二人轮流摸球,每次任意摸出一个球再放回,如果摸到的球的编号是质数,小红得1分;如果摸到的球的编号是合数,小明得1分;如果摸到的球的编号既不是质数也不是合数,两人都不得分。你认为这个游戏规则公平吗?
18.有一个棱长1米的正方体木块,它的6个面都涂有红色。把它切成棱长1分米的小正方体木块,没有涂红色的小正方体木块有 个。
19.一个长方体木块,先从左端截去长1.5cm的长方体,再从右端截去长3.5cm的长方体,这时剩下一个体积是64cm3的正方体,长方体木块的表面积减少了 cm2。
20.为庆祝“中国共产党百年华诞”准备节目,学校合唱社团需要舞蹈社团伴舞。舞蹈社团要4天排练一次,合唱社团要6天排练一次,每逢两个社团同时排练的日子需要在一起合练。5月7日两个社团第一次在一起合练,7月1日演出之前的最后一次合练是6月 日。
21.如图(图中单位:厘米),1个大球的体积是 立方厘米。
三、根据统计图回答问题。
22.2018年6月,国务院发布了《打赢蓝天保卫战三年行动计划》。北京空气质量持续改善,留住了越来越多的“北京蓝”。如图是根据“北京市生态环境局”网站提供的数据制作的统计图。
①2019年 月的达标天数上升得最快。在这一年中,有连续三个月的空气质量达标天数都是 天。
②2020年共有 个月的空气质量达标天数超过了2019年达标天数的最高标准,其中 月每天的空气质量都达标了。
③这两年,从3月到6月空气质量达标天数的变化都呈 趋势。
四、计算。
23.计算。
(1)+++ (2)+++
(3)﹣+﹣ (4)+(﹣)
五、解方程。
24.解方程。
+x=
六、解决问题。
25.自2020年5月1日起,《北京市生活垃圾管理条例》正式颁布。某小区一天产生的可回收物中废旧纺织物约占,废纸张约占,废塑料瓶约占。其余的约占几分之几?
26.超市要做一个长2.8米,宽0.4米,高0.8米的玻璃柜台。需要先用角铁做一个长方体框架再安装玻璃。至少需要多少米的角铁?
27.尽管一张纸很薄,但它也是一个长方体。已知一包A4复印纸高5厘米,请你根据图中提供的信息,计算出一张A4复印纸的体积是多少立方厘米?(最后得数保留整数)
28.2020年1月,国家发布了《关于进一步加强塑料污染治理的意见》。对于餐饮打包外卖服务、商超、药店等领域塑料制品禁限提出了要求。不可降解的塑料袋可以用纸袋、无纺布袋等替代。制作一个无纺布袋(如图),需要多少无纺布?(重叠部分和提手需4.8平方分米的无纺布)
29.机场托运的行李一般不超过如图所示的规格。张叔叔的行李是0.27m3的长方体包装箱,底面的长是60cm,宽是45cm。这个包装箱符合机场托运的一般规格吗?
2020-2021学年北京市丰台区五年级(下)期末数学试卷
参考答案与试题解析
一、选择正确答案,将选项涂在答题纸上(每题只有一个正确答案)。
1.【分析】根据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数(为了方便,我们在研究因数和倍数时,所说的数一般指不是零的自然数);由此进行选择即可。
【解答】解:根据因数和倍数的意义可知:
A、24÷3=8,能整除,所以24和3是因数和倍数关系;
B、1.8÷6=0.3,1.8和0.3都是小数,所以1.8和6不是因数和倍数的关系;
C、7÷2=3......1,所以不是因数和倍数关系;
D、12÷5=2......2,所以不是因数和倍数关系。
故选:A。
【点评】此题考查了因数和倍数的意义,要熟练掌握。
2.【分析】找一个数的倍数,直接把这个数分别乘以1、2、3、4、5、6.......,从而选择与题意相符的数即可。
【解答】解:7×2=14
7×3=21
7×4=28
7×5=35
因此符合题意的7的倍数有14,21,28和35这4个数。
故选:B。
【点评】本题考查了找7的倍数的方法。
3.【分析】假设这两个质数分别是a和b,它们的乘积是ab,ab的因数有1,a,b,ab,共4个因数。
【解答】解:假设这两个质数分别是a和b,
它们的乘积是ab,
ab的因数有1,a,b,ab,共4个因数;
所以,两个不同质数的乘积一共有4个因数。
故选:D。
【点评】本题考查质数和因数知识点,运用质数和因数的知识解决问题。
4.【分析】个位上是0或5的数是5的倍数;如果一个数的各个数位上的数的和是3的倍数,那么这个数就是3的倍数。
【解答】解:方框里应该填的数不是0就是5
4+0+3+0=7,7不是3的倍数,不合题意;
4+0+3+5=12,12是3的倍数,符合题意。
所以方框里应该填5。
故选:C。
【点评】熟练掌握3、5的倍数的特征是解题的关键。
5.【分析】求两数的最小公倍数,就看两个数之间的关系,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积。
【解答】解:因为a是正整数,所以a和a+1是相邻的正整数,它们是互质数,所以a和a+1的最小公倍数是a(a+1),最大公因数是1。
a(a+1)÷1=a(a+1)
所以a和a+1的最小公倍数是它们最大公因数的a(a+1)倍。
故选:D。
【点评】明确互质数的两个数的最大公因数是1,最小公倍数是这两个数的乘积是解题的关键。
6.【分析】根据实际情况,小朋友的拳头的体积应该小于1立方分米,据此解答即可。
【解答】解:由分析可知,拳头伸进盛满水的盆中,溢出来的水的体积小于1立方分米,即小于1升。
故选:B。
【点评】溢出来的水的体积就等于拳头的体积,据此解答即可。
7.【分析】令a+=b+=c+=d+=1,分别求出a、b、c、d的值,再比较a、b、c、d的大小即可。
【解答】解:令a+=b+=c+=d+=1
所以a=,b=,c=,d=
所以a>b>c>d
故选:A。
【点评】解决此题也可以比较的大小,哪个数最小,相应的另一个加数就越大。
8.【分析】分子大于或等于分母的分数是假分数,假分数的值大于或等于1,据此解答即可。
【解答】解:是假分数,所以≥1,a≥6
也是假分数,所以≥1,a≥9
因为a表示同一个数,所以a最小是9
所以
故选:C。
【点评】熟练掌握假分数的概念及特征是解题的关键。
9.【分析】N点在和之间,所以与每个选项逐一比较即可。
【解答】解:,,故C和D项排除;
,故A项排除;
,故B项符合要求。
故选:B。
【点评】此题重点考查用数轴上的点表示数的方法。
10.【分析】一块木板截去了分米,还剩下这块木板的,所以用单位“1”减去剩下的就是截去的这块木板的几分之几,再和比较即可。
【解答】解:1﹣=
所以剩下的部分大。
故选:C。
【点评】求出截去了这块木板的几分之几是解题的关键。
11.【分析】根据正方体展开图的11种特征,图A属于正方体展开图的“1﹣4﹣1”型,能折成正方体;图B不属于正方体展开图,不能折成正方体;图C属于正方体展开图的“2﹣2﹣2”型,能折成正方体;图D属于长方体展开图的“1﹣4﹣1”形,能折成长方体。
【解答】解:沿着虚线不能折成长方体或正方体的是图。
故选:B。
【点评】正方体、长方体展开图,都分“1﹣4﹣1”型、“1﹣3﹣2”型、“2﹣2﹣2”型和“3﹣3”型。正方体展开图有11种情况,长、宽、高不相等的长方体比较复杂,有54种情况。
12.【分析】通过观察图形可知,图B的表面积比图A增加了小正方体的4个面的面积;图C的表面积比图A增加了小正方体的2个面的面积;图D的表面积比图A增加了小正方体的4个面的面积;然后进行比较即可。
【解答】解:图B的表面积比图A增加了小正方体的4个面的面积;图C的表面积比图A增加了小正方体的2个面的面积;图D的表面积比图A增加了小正方体的4个面的面积。
2<4
所以图C的表面积最小。
故选:C。
【点评】此题考查的目的是理解掌握立体图形的拼组方法及应用,表面积的意义及应用。
二、填空。
13.【分析】立方厘米与毫升是同一级单位二者互化数值不变;
低级单位分化高级单位时除以进率60。
【解答】解:750mL=750cm3
15分=时
故答案为:750,。
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。结果用分数表示时,通常化成最简分数。
14.【分析】把0.6化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据分数与除法的关系=3÷5(此步答案不唯一).
【解答】解:0.6=3÷5=.
故答案为:3,5,12
【点评】此题主要是考查除法、小数、分数之间的关系及转化.利用它们之间的关系和性质进行转化即可.
15.【分析】根据正方体的体积公式:V=a3,把数据代入公式分别求出棱长1分米、棱长1厘米的正方体的体积,再根据“包含”除法的意义,用除法求出可以分成的块数,把这些小正方体木块摆成一排,成为一个长方体,这个长方体的长是1000厘米,宽和高都是1厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:1×1×1=1(立方分米)
1立方分米=1000立方厘米
1×1×1=1(立方厘米)
1000÷1=1000(块)
1000×1×4+1×1×2
=4000+2
=4002(平方厘米)
答:这个长方体的表面积是4002平方厘米。
故答案为:4002。
【点评】此题主要考查正方体的体积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
16.【分析】先把每个分数化成最简分数,一个最简分数,如果分母中除了2或5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数;根据分数化成小数的方法,用分数的分子除以分母;据此解答即可。
【解答】解:的分母中有质因数3,不能化成有限小数;
的分母中只含有质因数5,能化成有限小数;=11÷25=0.44。
故答案为:、0.44。
【点评】此题主要考查了小数与分数互化的方法,要熟练掌握,解答此题的关键是要明确:一个最简分数,如果分母中除了2或5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。
17.【分析】1~9中质数有2、3、5、7,合数有4、6、8、9,1既不是质数也不是合数,所以小红和小明得分的可能性相同,游戏规则公平。
【解答】解:质数有2、3、5、7;
合数有4、6、8、9;
所以小红和小明得分的可能性相同,游戏规则公平。
故答案为:公平。
【点评】解答此题的关键是要熟练掌握10以内的质数和合数,可能性相同,游戏就公平。
18.【分析】1米=10分米,因为10÷1=10(个),所以大正方体每条棱长上面都有10个小正方体;根据立体图形的切拼知识可知:三个面均为红色的是各顶点处的小正方体,在各棱上,除去顶点处的正方体的有两面红色,在每个面上,除去棱上的正方体都是一面红色,没有涂色的小正方体处在内部;根据上面的结论,据此即可解答问题。
【解答】解:1米=10分米
10÷1=10(个)
(10﹣2)×(10﹣2)×(10﹣2)
=8×8×8
=512(个)
答:没有涂红色的小正方体木块有512个。
故答案为:512。
【点评】抓住表面涂色的正方体切割小正方体的特点:1面涂色的在面上,2面涂色的在棱长上(除去顶点处的),3面涂色的在顶点处,没有涂色的在内部,由此即可解决此类问题。
19.【分析】根据剩下一个体积是64cm3的正方体,可以求出正方体的棱长是4cm,用正方体的棱长加上1.5cm,再加上3.5cm,求原长方体的长,再根据长方体的表面积公式S=(ab+ah+bh)×2、正方体的表面积公式S=6a2;进行解答即可。
【解答】解:体积是64cm3的正方体的棱长是4cm
4+1.5+3.5=9(cm)
(9×4+9×4+4×4)×2﹣4×4×6
=(36+36+16)×2﹣96
=88×2﹣96
=176﹣96
=80(cm2)
答:长方体木块的表面积减少了80cm2。
【点评】解答此题的关键是先求出原来长方体的长,进而利用长方体、正方体的表面积公式求解。
20.【分析】根据题意求出4和6的最小公倍数,先求得最小公倍数是12,然后把时间按照往后加12天方法进行时间的推理即可。注意5、6月份的是大月还是小月。
【解答】解:4和6的最小公倍数是12。
7+12=19,第二次排练时间是5月19日;
19+12=31。第三次排练时间是5月31日
5月31日+12=6月12日,第四次排练时间是6月12日;
6月12日+12=6月24日,第五次排练时间是6月24日,因为6月只有30天,因此往后比赛前就没有共同排练时间了,这是最后一次的排练时间。
故答案为:24。
【点评】解答本题的关键是:理解他们从5月7日到每次排练的时间是4和6的最小公倍数,再根据年月日的知识,找出5、6月里的天数。
21.【分析】比较图二和图三可得5个小球的体积是长方体中(10﹣5)厘米高的水的体积,据此计算出1个小球的体积;比图一和图二可得2个大球和一个小球的体积是长方体中5厘米高水的体积;据此进一步解答即可。
【解答】解:6×6×(10﹣5)÷5
=36×5÷5
=36(立方厘米)
6×6×5
=36×5
=180(立方厘米)
(180﹣36)÷2
=144÷2
=72(立方厘米)
答:1个大球的体积是72立方厘米。
故答案为:72。
【点评】本题主要考查排水法测量物体体积知识点,浸没入水中的物体体积=排开的水的体积。
三、根据统计图回答问题。
22.【分析】复式折线统计图中,横轴表示月份,纵轴表示空气质量达标天数,虚线表示2019年空气质量达标天数的情况,实线表示2020年空气质量达标天数的情况;
①2019年向右上延伸的线段中,7~8月的坡度最大,说明8月达标天数上升得最快;2019年10、11、12月连续三个月空气质量达标天数都是25天;
②2019天达标天数的最高标准是25天,2020年月达标天数超过25天的有3月、9月、12月这3个月,其中12月共31天,达标天数也是31天,每天的空气质量都达标了;
③这两年的3~6月,线段都向右下延伸,说明空气质量达标天数呈下降趋势。
【解答】解:①2019年8月的达标天数上升得最快。在这一年中,有连续三个月的空气质量达标天数都是25天。
②2020年共有3个月的空气质量达标天数超过了2019年达标天数的最高标准,其中12月每天的空气质量都达标了。
③这两年,从3月到6月空气质量达标天数的变化都呈下降趋势。
故答案为:8,25;3,12;下降。
【点评】此题重点考查从复式折线统计图中获取信息进行分析的能力。
四、计算。
23.【分析】(1),,,;据此运用简便方法计算;
(2)运用加法交换律和结合律进行简便运算;
(3)运用加法交换律和减法的性质进行简便运算;
(4)按运算顺序计算。
【解答】解:(1)+++
=(1﹣)+(﹣)+(﹣)+(﹣)
=1﹣+﹣+﹣+﹣
=1﹣
=
(2)+++
=++(+)
=1+1
=2
(3)﹣+﹣
=+﹣(+)
=1﹣
=
(4)+(﹣)
=
=1
【点评】本题考查分数的四则混合运算和运算定律,注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五、解方程。
24.【分析】根据等式的基本性质,方程两边同时减去即可。
【解答】解: +x=
+x﹣=﹣
x=
【点评】熟练掌握等式的基本性质是解题的关键。
六、解决问题。
25.【分析】把该小区一天回收的垃圾总量看作单位“1”,根据求剩余问题的方法,用减法解答。
【解答】解:1
=1﹣
=
答:其余的约占。
【点评】此题考查的目的是理解分数减法的意义,掌握分数减法的计算法则及应用。
26.【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答。
【解答】解:(2.8+0.4+0.8)×4
=4×4
=16(米)
答:至少需要16米的角铁。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和公式的灵活运用,关键是熟记公式。
27.【分析】根据长方体的体积公式:V=abh,把数据代入公式求出一包(500张)纸的体积,然后除以500就是一张纸的体积。
【解答】解:210毫米=21厘米
297毫米=29.7厘米
21×29.7×5÷500
=623.7×5÷500
=3118.5÷500
≈6(立方厘米)
答:一张A4复印纸的体积是6立方厘米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
28.【分析】根据长方体的表面积公式,求出5个面的面积,再加上重叠部分和提手的面积即可解答。
【解答】解:3×1+3×4×2+1×4×2+4.8
=3+24+8+4.8
=39.8(平方分米)
答:需要39.8平方分米的无纺布。
【点评】此题主要考查长方体的表面积公式的灵活运用。
29.【分析】根据长方体的体积公式:V=abh,那么h=V÷a÷b,据此求出张叔叔的行李的高,然后与90厘米进行比较,如果行李的高小于或等于90厘米,说明符合机场托运的一般规格,否则就不符合。
【解答】解:0.27立方米=270000立方厘米
270000÷60÷45
=4500÷45
=100(厘米)
100>90
答:这个包装箱不符合机场托运的一般规格。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
一、选择正确答案,将选项涂在答题纸上(每题只有一个正确答案)。
1.在下面每组数中,有因数和倍数关系的是( )
A.3和24 B.1.8和6 C.2和7 D.12和5
2.在10到40中,7的倍数共有( )个。
A.3 B.4 C.5 D.6
3.两个不同质数的乘积一共有( )个因数。
A.1 B.2 C.3 D.4
4.在“403□”的方框里填个数,使这个四位数既是5的倍数,又有因数3,方框里应该填( )
A.0 B.2 C.5 D.8
5.a为正整数,则a和a+1的最小公倍数是它们最大公因数的( )倍。
A.1 B.a C.a+1 D.a (a+1)
6.把你的拳头伸进盛满水的盆中,溢出来的水的体积( )
A.小于10毫升 B.小于1升 C.等于1升 D.大于1升
7.如果a+=b+=c+=d+,那么在a、b、c、d中,最大的数是( )
A.a B.b C.c D.d
8.是假分数,也是假分数。如果a表示同一个数,那么这两个分数的和一定( )
A.小于2 B.等于2 C.大于2 D.不小于2
9.如图中N点表示的数是( )
A. B. C. D.
10.一块木板截去了平方分米,还剩下这块木板的。下面说法正确的是( )
A.两部分同样大 B.截去的部分大
C.剩下的部分大 D.剩下平方分米
11.下面的折纸材料中,沿着虚线不能折成长方体或正方体的是图( )
A. B.
C. D.
12.在模型A的基础上添加一个小正方体后得到模型B、C、D,模型B、C、D中,( )的表面积最小。
A. B. C. D.
二、填空。
13.750mL= cm3
15分=时
14.0.6= ÷ =
15.把棱长1分米的正方体木块分成棱长是1厘米的小正方体木块后,再把这些小正方体木块摆成一排,成为一个长方体。这个长方体的表面积是 平方厘米。
16.在、中,能化成有限小数的是 ,化成的有限小数是 。
17.把九个完全相同的球,先按照1~9编号,然后放进盒子里。小红和小明玩摸球游戏,规定二人轮流摸球,每次任意摸出一个球再放回,如果摸到的球的编号是质数,小红得1分;如果摸到的球的编号是合数,小明得1分;如果摸到的球的编号既不是质数也不是合数,两人都不得分。你认为这个游戏规则公平吗?
18.有一个棱长1米的正方体木块,它的6个面都涂有红色。把它切成棱长1分米的小正方体木块,没有涂红色的小正方体木块有 个。
19.一个长方体木块,先从左端截去长1.5cm的长方体,再从右端截去长3.5cm的长方体,这时剩下一个体积是64cm3的正方体,长方体木块的表面积减少了 cm2。
20.为庆祝“中国共产党百年华诞”准备节目,学校合唱社团需要舞蹈社团伴舞。舞蹈社团要4天排练一次,合唱社团要6天排练一次,每逢两个社团同时排练的日子需要在一起合练。5月7日两个社团第一次在一起合练,7月1日演出之前的最后一次合练是6月 日。
21.如图(图中单位:厘米),1个大球的体积是 立方厘米。
三、根据统计图回答问题。
22.2018年6月,国务院发布了《打赢蓝天保卫战三年行动计划》。北京空气质量持续改善,留住了越来越多的“北京蓝”。如图是根据“北京市生态环境局”网站提供的数据制作的统计图。
①2019年 月的达标天数上升得最快。在这一年中,有连续三个月的空气质量达标天数都是 天。
②2020年共有 个月的空气质量达标天数超过了2019年达标天数的最高标准,其中 月每天的空气质量都达标了。
③这两年,从3月到6月空气质量达标天数的变化都呈 趋势。
四、计算。
23.计算。
(1)+++ (2)+++
(3)﹣+﹣ (4)+(﹣)
五、解方程。
24.解方程。
+x=
六、解决问题。
25.自2020年5月1日起,《北京市生活垃圾管理条例》正式颁布。某小区一天产生的可回收物中废旧纺织物约占,废纸张约占,废塑料瓶约占。其余的约占几分之几?
26.超市要做一个长2.8米,宽0.4米,高0.8米的玻璃柜台。需要先用角铁做一个长方体框架再安装玻璃。至少需要多少米的角铁?
27.尽管一张纸很薄,但它也是一个长方体。已知一包A4复印纸高5厘米,请你根据图中提供的信息,计算出一张A4复印纸的体积是多少立方厘米?(最后得数保留整数)
28.2020年1月,国家发布了《关于进一步加强塑料污染治理的意见》。对于餐饮打包外卖服务、商超、药店等领域塑料制品禁限提出了要求。不可降解的塑料袋可以用纸袋、无纺布袋等替代。制作一个无纺布袋(如图),需要多少无纺布?(重叠部分和提手需4.8平方分米的无纺布)
29.机场托运的行李一般不超过如图所示的规格。张叔叔的行李是0.27m3的长方体包装箱,底面的长是60cm,宽是45cm。这个包装箱符合机场托运的一般规格吗?
2020-2021学年北京市丰台区五年级(下)期末数学试卷
参考答案与试题解析
一、选择正确答案,将选项涂在答题纸上(每题只有一个正确答案)。
1.【分析】根据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数(为了方便,我们在研究因数和倍数时,所说的数一般指不是零的自然数);由此进行选择即可。
【解答】解:根据因数和倍数的意义可知:
A、24÷3=8,能整除,所以24和3是因数和倍数关系;
B、1.8÷6=0.3,1.8和0.3都是小数,所以1.8和6不是因数和倍数的关系;
C、7÷2=3......1,所以不是因数和倍数关系;
D、12÷5=2......2,所以不是因数和倍数关系。
故选:A。
【点评】此题考查了因数和倍数的意义,要熟练掌握。
2.【分析】找一个数的倍数,直接把这个数分别乘以1、2、3、4、5、6.......,从而选择与题意相符的数即可。
【解答】解:7×2=14
7×3=21
7×4=28
7×5=35
因此符合题意的7的倍数有14,21,28和35这4个数。
故选:B。
【点评】本题考查了找7的倍数的方法。
3.【分析】假设这两个质数分别是a和b,它们的乘积是ab,ab的因数有1,a,b,ab,共4个因数。
【解答】解:假设这两个质数分别是a和b,
它们的乘积是ab,
ab的因数有1,a,b,ab,共4个因数;
所以,两个不同质数的乘积一共有4个因数。
故选:D。
【点评】本题考查质数和因数知识点,运用质数和因数的知识解决问题。
4.【分析】个位上是0或5的数是5的倍数;如果一个数的各个数位上的数的和是3的倍数,那么这个数就是3的倍数。
【解答】解:方框里应该填的数不是0就是5
4+0+3+0=7,7不是3的倍数,不合题意;
4+0+3+5=12,12是3的倍数,符合题意。
所以方框里应该填5。
故选:C。
【点评】熟练掌握3、5的倍数的特征是解题的关键。
5.【分析】求两数的最小公倍数,就看两个数之间的关系,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积。
【解答】解:因为a是正整数,所以a和a+1是相邻的正整数,它们是互质数,所以a和a+1的最小公倍数是a(a+1),最大公因数是1。
a(a+1)÷1=a(a+1)
所以a和a+1的最小公倍数是它们最大公因数的a(a+1)倍。
故选:D。
【点评】明确互质数的两个数的最大公因数是1,最小公倍数是这两个数的乘积是解题的关键。
6.【分析】根据实际情况,小朋友的拳头的体积应该小于1立方分米,据此解答即可。
【解答】解:由分析可知,拳头伸进盛满水的盆中,溢出来的水的体积小于1立方分米,即小于1升。
故选:B。
【点评】溢出来的水的体积就等于拳头的体积,据此解答即可。
7.【分析】令a+=b+=c+=d+=1,分别求出a、b、c、d的值,再比较a、b、c、d的大小即可。
【解答】解:令a+=b+=c+=d+=1
所以a=,b=,c=,d=
所以a>b>c>d
故选:A。
【点评】解决此题也可以比较的大小,哪个数最小,相应的另一个加数就越大。
8.【分析】分子大于或等于分母的分数是假分数,假分数的值大于或等于1,据此解答即可。
【解答】解:是假分数,所以≥1,a≥6
也是假分数,所以≥1,a≥9
因为a表示同一个数,所以a最小是9
所以
故选:C。
【点评】熟练掌握假分数的概念及特征是解题的关键。
9.【分析】N点在和之间,所以与每个选项逐一比较即可。
【解答】解:,,故C和D项排除;
,故A项排除;
,故B项符合要求。
故选:B。
【点评】此题重点考查用数轴上的点表示数的方法。
10.【分析】一块木板截去了分米,还剩下这块木板的,所以用单位“1”减去剩下的就是截去的这块木板的几分之几,再和比较即可。
【解答】解:1﹣=
所以剩下的部分大。
故选:C。
【点评】求出截去了这块木板的几分之几是解题的关键。
11.【分析】根据正方体展开图的11种特征,图A属于正方体展开图的“1﹣4﹣1”型,能折成正方体;图B不属于正方体展开图,不能折成正方体;图C属于正方体展开图的“2﹣2﹣2”型,能折成正方体;图D属于长方体展开图的“1﹣4﹣1”形,能折成长方体。
【解答】解:沿着虚线不能折成长方体或正方体的是图。
故选:B。
【点评】正方体、长方体展开图,都分“1﹣4﹣1”型、“1﹣3﹣2”型、“2﹣2﹣2”型和“3﹣3”型。正方体展开图有11种情况,长、宽、高不相等的长方体比较复杂,有54种情况。
12.【分析】通过观察图形可知,图B的表面积比图A增加了小正方体的4个面的面积;图C的表面积比图A增加了小正方体的2个面的面积;图D的表面积比图A增加了小正方体的4个面的面积;然后进行比较即可。
【解答】解:图B的表面积比图A增加了小正方体的4个面的面积;图C的表面积比图A增加了小正方体的2个面的面积;图D的表面积比图A增加了小正方体的4个面的面积。
2<4
所以图C的表面积最小。
故选:C。
【点评】此题考查的目的是理解掌握立体图形的拼组方法及应用,表面积的意义及应用。
二、填空。
13.【分析】立方厘米与毫升是同一级单位二者互化数值不变;
低级单位分化高级单位时除以进率60。
【解答】解:750mL=750cm3
15分=时
故答案为:750,。
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。结果用分数表示时,通常化成最简分数。
14.【分析】把0.6化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据分数与除法的关系=3÷5(此步答案不唯一).
【解答】解:0.6=3÷5=.
故答案为:3,5,12
【点评】此题主要是考查除法、小数、分数之间的关系及转化.利用它们之间的关系和性质进行转化即可.
15.【分析】根据正方体的体积公式:V=a3,把数据代入公式分别求出棱长1分米、棱长1厘米的正方体的体积,再根据“包含”除法的意义,用除法求出可以分成的块数,把这些小正方体木块摆成一排,成为一个长方体,这个长方体的长是1000厘米,宽和高都是1厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:1×1×1=1(立方分米)
1立方分米=1000立方厘米
1×1×1=1(立方厘米)
1000÷1=1000(块)
1000×1×4+1×1×2
=4000+2
=4002(平方厘米)
答:这个长方体的表面积是4002平方厘米。
故答案为:4002。
【点评】此题主要考查正方体的体积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
16.【分析】先把每个分数化成最简分数,一个最简分数,如果分母中除了2或5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数;根据分数化成小数的方法,用分数的分子除以分母;据此解答即可。
【解答】解:的分母中有质因数3,不能化成有限小数;
的分母中只含有质因数5,能化成有限小数;=11÷25=0.44。
故答案为:、0.44。
【点评】此题主要考查了小数与分数互化的方法,要熟练掌握,解答此题的关键是要明确:一个最简分数,如果分母中除了2或5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。
17.【分析】1~9中质数有2、3、5、7,合数有4、6、8、9,1既不是质数也不是合数,所以小红和小明得分的可能性相同,游戏规则公平。
【解答】解:质数有2、3、5、7;
合数有4、6、8、9;
所以小红和小明得分的可能性相同,游戏规则公平。
故答案为:公平。
【点评】解答此题的关键是要熟练掌握10以内的质数和合数,可能性相同,游戏就公平。
18.【分析】1米=10分米,因为10÷1=10(个),所以大正方体每条棱长上面都有10个小正方体;根据立体图形的切拼知识可知:三个面均为红色的是各顶点处的小正方体,在各棱上,除去顶点处的正方体的有两面红色,在每个面上,除去棱上的正方体都是一面红色,没有涂色的小正方体处在内部;根据上面的结论,据此即可解答问题。
【解答】解:1米=10分米
10÷1=10(个)
(10﹣2)×(10﹣2)×(10﹣2)
=8×8×8
=512(个)
答:没有涂红色的小正方体木块有512个。
故答案为:512。
【点评】抓住表面涂色的正方体切割小正方体的特点:1面涂色的在面上,2面涂色的在棱长上(除去顶点处的),3面涂色的在顶点处,没有涂色的在内部,由此即可解决此类问题。
19.【分析】根据剩下一个体积是64cm3的正方体,可以求出正方体的棱长是4cm,用正方体的棱长加上1.5cm,再加上3.5cm,求原长方体的长,再根据长方体的表面积公式S=(ab+ah+bh)×2、正方体的表面积公式S=6a2;进行解答即可。
【解答】解:体积是64cm3的正方体的棱长是4cm
4+1.5+3.5=9(cm)
(9×4+9×4+4×4)×2﹣4×4×6
=(36+36+16)×2﹣96
=88×2﹣96
=176﹣96
=80(cm2)
答:长方体木块的表面积减少了80cm2。
【点评】解答此题的关键是先求出原来长方体的长,进而利用长方体、正方体的表面积公式求解。
20.【分析】根据题意求出4和6的最小公倍数,先求得最小公倍数是12,然后把时间按照往后加12天方法进行时间的推理即可。注意5、6月份的是大月还是小月。
【解答】解:4和6的最小公倍数是12。
7+12=19,第二次排练时间是5月19日;
19+12=31。第三次排练时间是5月31日
5月31日+12=6月12日,第四次排练时间是6月12日;
6月12日+12=6月24日,第五次排练时间是6月24日,因为6月只有30天,因此往后比赛前就没有共同排练时间了,这是最后一次的排练时间。
故答案为:24。
【点评】解答本题的关键是:理解他们从5月7日到每次排练的时间是4和6的最小公倍数,再根据年月日的知识,找出5、6月里的天数。
21.【分析】比较图二和图三可得5个小球的体积是长方体中(10﹣5)厘米高的水的体积,据此计算出1个小球的体积;比图一和图二可得2个大球和一个小球的体积是长方体中5厘米高水的体积;据此进一步解答即可。
【解答】解:6×6×(10﹣5)÷5
=36×5÷5
=36(立方厘米)
6×6×5
=36×5
=180(立方厘米)
(180﹣36)÷2
=144÷2
=72(立方厘米)
答:1个大球的体积是72立方厘米。
故答案为:72。
【点评】本题主要考查排水法测量物体体积知识点,浸没入水中的物体体积=排开的水的体积。
三、根据统计图回答问题。
22.【分析】复式折线统计图中,横轴表示月份,纵轴表示空气质量达标天数,虚线表示2019年空气质量达标天数的情况,实线表示2020年空气质量达标天数的情况;
①2019年向右上延伸的线段中,7~8月的坡度最大,说明8月达标天数上升得最快;2019年10、11、12月连续三个月空气质量达标天数都是25天;
②2019天达标天数的最高标准是25天,2020年月达标天数超过25天的有3月、9月、12月这3个月,其中12月共31天,达标天数也是31天,每天的空气质量都达标了;
③这两年的3~6月,线段都向右下延伸,说明空气质量达标天数呈下降趋势。
【解答】解:①2019年8月的达标天数上升得最快。在这一年中,有连续三个月的空气质量达标天数都是25天。
②2020年共有3个月的空气质量达标天数超过了2019年达标天数的最高标准,其中12月每天的空气质量都达标了。
③这两年,从3月到6月空气质量达标天数的变化都呈下降趋势。
故答案为:8,25;3,12;下降。
【点评】此题重点考查从复式折线统计图中获取信息进行分析的能力。
四、计算。
23.【分析】(1),,,;据此运用简便方法计算;
(2)运用加法交换律和结合律进行简便运算;
(3)运用加法交换律和减法的性质进行简便运算;
(4)按运算顺序计算。
【解答】解:(1)+++
=(1﹣)+(﹣)+(﹣)+(﹣)
=1﹣+﹣+﹣+﹣
=1﹣
=
(2)+++
=++(+)
=1+1
=2
(3)﹣+﹣
=+﹣(+)
=1﹣
=
(4)+(﹣)
=
=1
【点评】本题考查分数的四则混合运算和运算定律,注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五、解方程。
24.【分析】根据等式的基本性质,方程两边同时减去即可。
【解答】解: +x=
+x﹣=﹣
x=
【点评】熟练掌握等式的基本性质是解题的关键。
六、解决问题。
25.【分析】把该小区一天回收的垃圾总量看作单位“1”,根据求剩余问题的方法,用减法解答。
【解答】解:1
=1﹣
=
答:其余的约占。
【点评】此题考查的目的是理解分数减法的意义,掌握分数减法的计算法则及应用。
26.【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答。
【解答】解:(2.8+0.4+0.8)×4
=4×4
=16(米)
答:至少需要16米的角铁。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和公式的灵活运用,关键是熟记公式。
27.【分析】根据长方体的体积公式:V=abh,把数据代入公式求出一包(500张)纸的体积,然后除以500就是一张纸的体积。
【解答】解:210毫米=21厘米
297毫米=29.7厘米
21×29.7×5÷500
=623.7×5÷500
=3118.5÷500
≈6(立方厘米)
答:一张A4复印纸的体积是6立方厘米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
28.【分析】根据长方体的表面积公式,求出5个面的面积,再加上重叠部分和提手的面积即可解答。
【解答】解:3×1+3×4×2+1×4×2+4.8
=3+24+8+4.8
=39.8(平方分米)
答:需要39.8平方分米的无纺布。
【点评】此题主要考查长方体的表面积公式的灵活运用。
29.【分析】根据长方体的体积公式:V=abh,那么h=V÷a÷b,据此求出张叔叔的行李的高,然后与90厘米进行比较,如果行李的高小于或等于90厘米,说明符合机场托运的一般规格,否则就不符合。
【解答】解:0.27立方米=270000立方厘米
270000÷60÷45
=4500÷45
=100(厘米)
100>90
答:这个包装箱不符合机场托运的一般规格。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
同课章节目录
