沪科版数学八年级上册 12.1函数 第3课时 同步课件(共20张)
文档属性
| 名称 | 沪科版数学八年级上册 12.1函数 第3课时 同步课件(共20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 875.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 13:38:58 | ||
图片预览






文档简介
(共20张PPT)
第十二章 一次函数
12.1 函数(第3课时)
知识回顾
1.表示函数关系的方法:列表法、解析法、图象法;
2.确定自变量的取值范围的方法:
(1)整式和奇次根式中,自变量的取值范围是全体实数;
(2)偶次根式中,被开方式大于或等于0;
(3)分式中,分母不能为0;
(4)零指数幂、负整数指数幂中,底数不为0;
(5)实际问题中,自变量除了满足解析式有意义外,还要考虑使实际问题有意义.
3.自变量的值与函数值.
获取新知
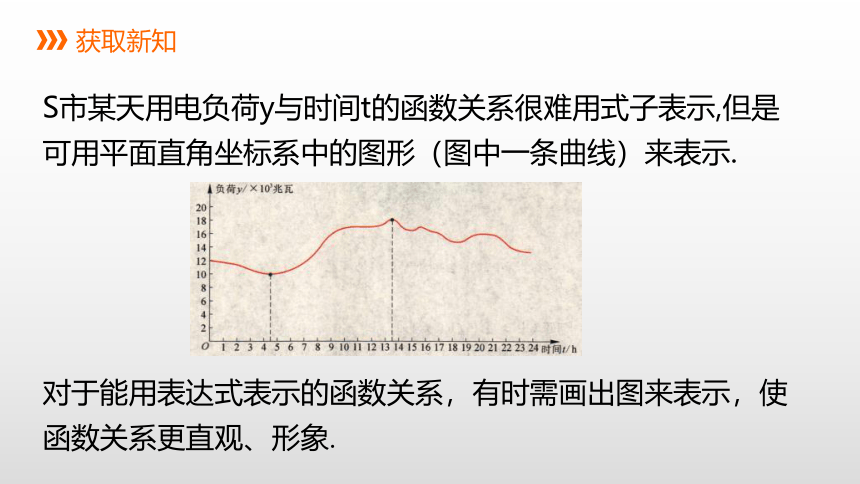
S市某天用电负荷y与时间t的函数关系很难用式子表示,但是可用平面直角坐标系中的图形(图中一条曲线)来表示.
对于能用表达式表示的函数关系,有时需画出图来表示,使函数关系更直观、形象.
如何作函数的图呢?
下面以作函数y=2x的图为例来说明.
画函数y=2x的图:
①列表:
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
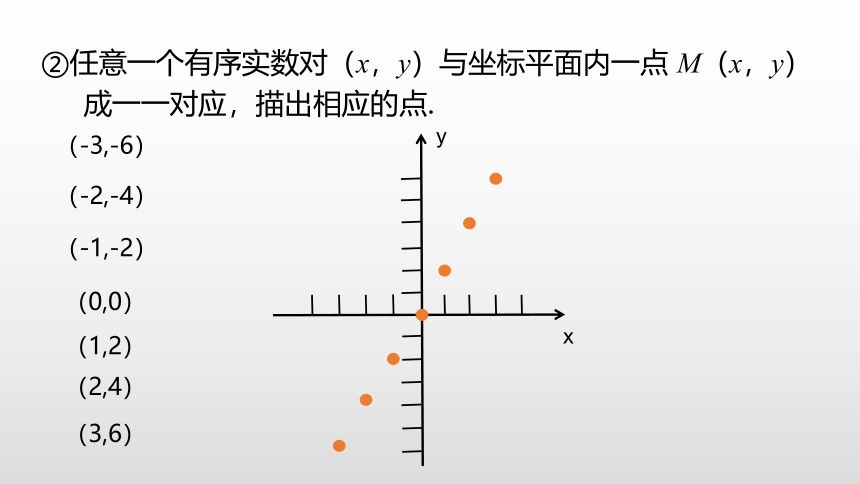
②任意一个有序实数对(x,y)与坐标平面内一点 M(x,y)
成一一对应,描出相应的点.
x
y
(-3,-6)
(-2,-4)
(-1,-2)
(0,0)
(1,2)
(2,4)
(3,6)
x
y
8
6
4
2
-2
-4
-6
-8
③无数个点组成了坐标系中的图形.
由函数表达式画图象,一般按下列步骤进行:
1. 列表:列表给出自变量与函数的一些对应值.
描点:以表中各组对应值为坐标,在坐标平面内描出
相应的点.
连线:按照自变量由小到大的顺序,把所描各点用平
滑曲线依次连接起来.
例题精讲
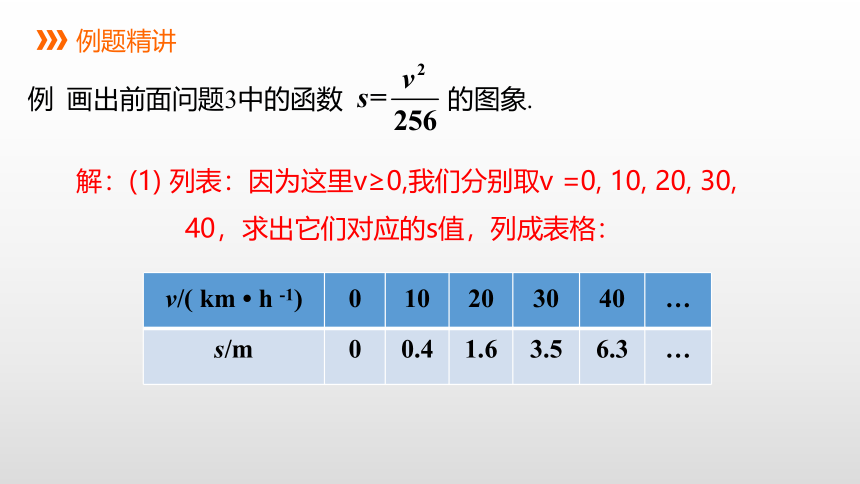
例 画出前面问题3中的函数 的图象.
解:(1) 列表:因为这里v≥0,我们分别取v =0, 10, 20, 30,
40,求出它们对应的s值,列成表格:
v/( km h -1) 0 10 20 30 40 …
s/m 0 0.4 1.6 3.5 6.3 …
描点:在坐标平面内描出(0, 0),(10, 0.4), (20, 1.6),
(30, 3.5),(40, 6.3)等点.
x
y
10
20
30
40
1
2
3
4
5
6
x
y
10
20
30
40
1
2
3
4
5
6
连线:将以上各点按照自变量由小到大的顺序用平
滑曲线连接,就得到了
例 已知函数y=2x-1.
(1)试判断点A(-1,3)和点B 是否在此函数的图
象上;
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
分析:(1)将点A,B的坐标分别代入y=2x-1,看点的坐标能否
满足这个表达式即可;(2)将点C的坐标代入y=2x-1,
可得到一个关于a的一元一次方程,求出a的值即可.
解:(1)因为当x=-1时,y=2×(-1)-1=-3≠3,
所以点A不在函数y=2x-1的图象上.
所以点B在函数y=2x-1的图象上.
(2)因为点C(a,a+1)在函数y=2x-1的图象上,
所以把x=a,y=a+1代入y=2x-1,得a+1=2a-1.
解得a=2.
(1)判断点P(x,y)是否在函数图象上的方法是:将点P(x,y)
的x,y值代入函数表达式,若能满足函数的表达式,则
这个点就在函数的图象上;若不满足函数的表达式,则
这个点不在函数的图象上.
(2)坐标含字母的点在函数图象上求字母值的方法:将坐标
代入函数表达式中,得到一个关于该字母的方程,解这
个方程即得字母的值.
课堂小结
图像法
列表
描点
连线
随堂演练
1.下列各点在函数y=3x-4的图象上的是( )
A.(-1,1) B.(2,2)
C.(-2,2) D.(2,-2)
2.已知点A(2,3)在函数y=ax+1的图象上,则a的值为( )
A.1 B.-1 C.2 D.-2
B
A
3.教材练习第3题变式题 下列四个图象分别给出了x与y的对应关系,其中y是x的函数的是( )
D
4.画出函数y=2x-1的图象,并判断点(1,1),(-1,0),(-2,3),(2,3)是否在该函数图象上.
解:列表:
x … -3 -2 -1 0 1 2 3 …
y … -7 -5 -3 -1 1 3 5 …
描点,并用平滑的曲线连接这些点,就得到函数y=2x-1的图象.
点(1,1),(2,3)在函数y=2x-1的图象上,点(-1,0),(-2,3)不在函数y=2x-1的图象上.
第十二章 一次函数
12.1 函数(第3课时)
知识回顾
1.表示函数关系的方法:列表法、解析法、图象法;
2.确定自变量的取值范围的方法:
(1)整式和奇次根式中,自变量的取值范围是全体实数;
(2)偶次根式中,被开方式大于或等于0;
(3)分式中,分母不能为0;
(4)零指数幂、负整数指数幂中,底数不为0;
(5)实际问题中,自变量除了满足解析式有意义外,还要考虑使实际问题有意义.
3.自变量的值与函数值.
获取新知
S市某天用电负荷y与时间t的函数关系很难用式子表示,但是可用平面直角坐标系中的图形(图中一条曲线)来表示.
对于能用表达式表示的函数关系,有时需画出图来表示,使函数关系更直观、形象.
如何作函数的图呢?
下面以作函数y=2x的图为例来说明.
画函数y=2x的图:
①列表:
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
②任意一个有序实数对(x,y)与坐标平面内一点 M(x,y)
成一一对应,描出相应的点.
x
y
(-3,-6)
(-2,-4)
(-1,-2)
(0,0)
(1,2)
(2,4)
(3,6)
x
y
8
6
4
2
-2
-4
-6
-8
③无数个点组成了坐标系中的图形.
由函数表达式画图象,一般按下列步骤进行:
1. 列表:列表给出自变量与函数的一些对应值.
描点:以表中各组对应值为坐标,在坐标平面内描出
相应的点.
连线:按照自变量由小到大的顺序,把所描各点用平
滑曲线依次连接起来.
例题精讲
例 画出前面问题3中的函数 的图象.
解:(1) 列表:因为这里v≥0,我们分别取v =0, 10, 20, 30,
40,求出它们对应的s值,列成表格:
v/( km h -1) 0 10 20 30 40 …
s/m 0 0.4 1.6 3.5 6.3 …
描点:在坐标平面内描出(0, 0),(10, 0.4), (20, 1.6),
(30, 3.5),(40, 6.3)等点.
x
y
10
20
30
40
1
2
3
4
5
6
x
y
10
20
30
40
1
2
3
4
5
6
连线:将以上各点按照自变量由小到大的顺序用平
滑曲线连接,就得到了
例 已知函数y=2x-1.
(1)试判断点A(-1,3)和点B 是否在此函数的图
象上;
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
分析:(1)将点A,B的坐标分别代入y=2x-1,看点的坐标能否
满足这个表达式即可;(2)将点C的坐标代入y=2x-1,
可得到一个关于a的一元一次方程,求出a的值即可.
解:(1)因为当x=-1时,y=2×(-1)-1=-3≠3,
所以点A不在函数y=2x-1的图象上.
所以点B在函数y=2x-1的图象上.
(2)因为点C(a,a+1)在函数y=2x-1的图象上,
所以把x=a,y=a+1代入y=2x-1,得a+1=2a-1.
解得a=2.
(1)判断点P(x,y)是否在函数图象上的方法是:将点P(x,y)
的x,y值代入函数表达式,若能满足函数的表达式,则
这个点就在函数的图象上;若不满足函数的表达式,则
这个点不在函数的图象上.
(2)坐标含字母的点在函数图象上求字母值的方法:将坐标
代入函数表达式中,得到一个关于该字母的方程,解这
个方程即得字母的值.
课堂小结
图像法
列表
描点
连线
随堂演练
1.下列各点在函数y=3x-4的图象上的是( )
A.(-1,1) B.(2,2)
C.(-2,2) D.(2,-2)
2.已知点A(2,3)在函数y=ax+1的图象上,则a的值为( )
A.1 B.-1 C.2 D.-2
B
A
3.教材练习第3题变式题 下列四个图象分别给出了x与y的对应关系,其中y是x的函数的是( )
D
4.画出函数y=2x-1的图象,并判断点(1,1),(-1,0),(-2,3),(2,3)是否在该函数图象上.
解:列表:
x … -3 -2 -1 0 1 2 3 …
y … -7 -5 -3 -1 1 3 5 …
描点,并用平滑的曲线连接这些点,就得到函数y=2x-1的图象.
点(1,1),(2,3)在函数y=2x-1的图象上,点(-1,0),(-2,3)不在函数y=2x-1的图象上.
