沪科版数学八年级上册12.2一次函数(第5课时)同步课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级上册12.2一次函数(第5课时)同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第十二章 一次函数
12.2 一次函数(第5课时)
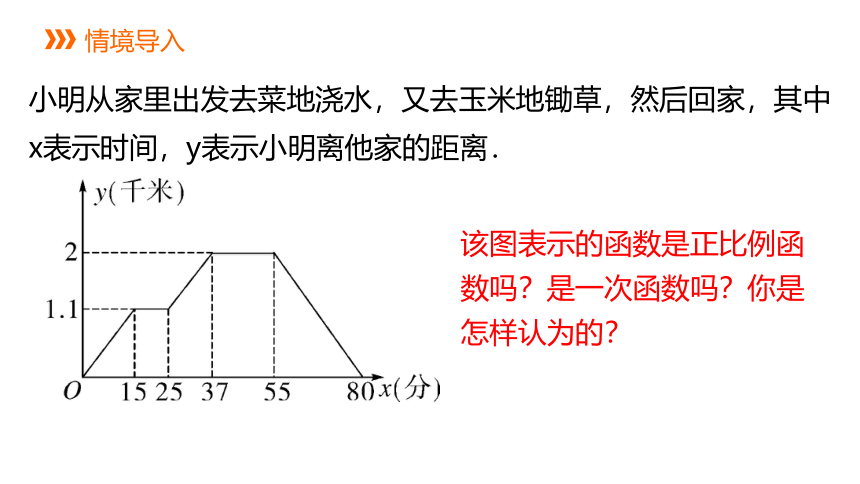
情境导入
小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.
该图表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
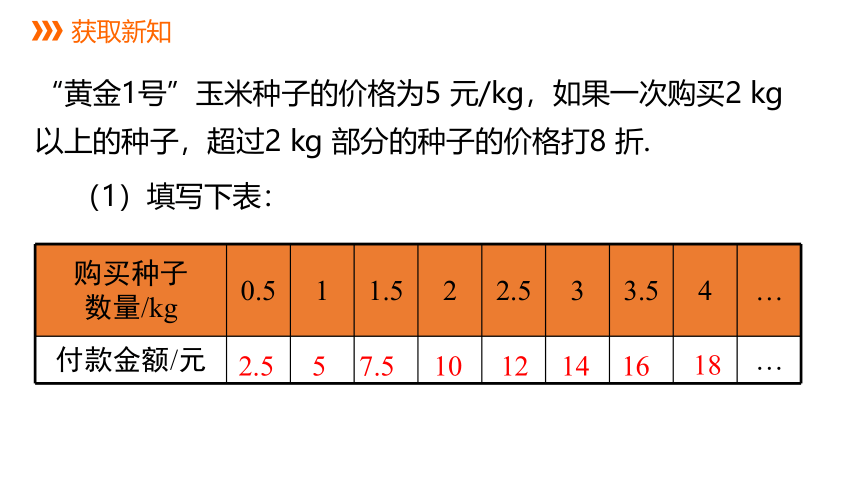
获取新知
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12
14
16
18
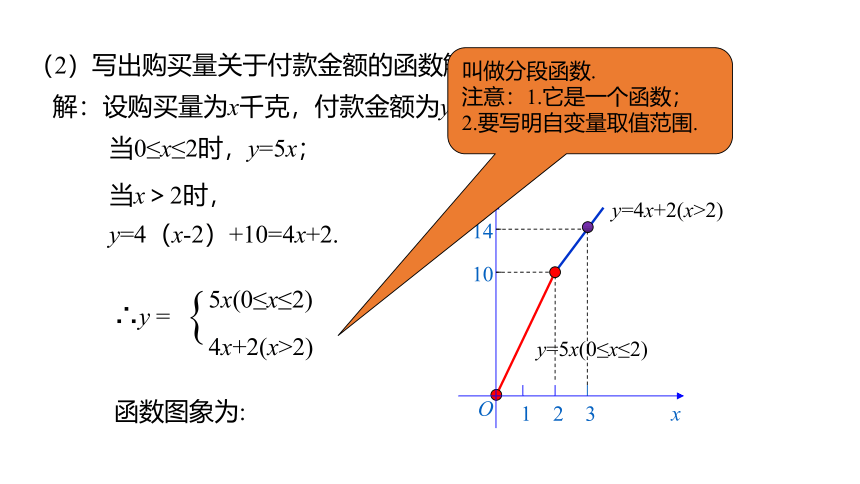
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
解:设购买量为x千克,付款金额为y元.
当x>2时,
y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
∴y =
5x(0≤x≤2)
4x+2(x>2)
函数图象为:
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
例题精讲
例 为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过8立方米时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数关系式;
解:(1)y关于x的函数关系式为
(1+0.3)x =1.3x (0≤x≤8),
(1.5+1.2)(x-8)+1.3 × 8=2.7x-11.2 (x>8);
y=
函数图象如图所示;
30
20
10
8
16
O
.
.
(8,10.4)
(16,32)
y/元
x/m3
(2)画出上述函数图象;
(3)该市某户某月若用水x=5立
方米或x=10立方米时,
求应缴水费;
(3)当x=5 m3时,
y=1.3×5=6.5(元);
当x=10m3时,y=2.7×10-11.2=15.8(元).
即当用水量为5m3时,该户应缴水费6.5元;当用水量为10m3时,该户应缴水费15.8元.
(4)y=26.6>1.3×8,可知该户这月用水超过8m3,
因此,2.7x-11.2=26.6,
解方程,得 x=14.
即该户本月用水量为14m3.
(4)该市某户某月缴水费26.6元,求该户这月用水量.
要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程.
课堂小结
分段函数
对分段函数图像的理解
分段函数的具体应用
随堂演练
1.目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数表达式是( )
A.y=0.05x B.y=5x
C.y=100x D.y=0.05x+100
B
2.2018·和县期末一个有进水管与出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则8 min时容器内的水量为( )
A.20 L B.25 L C.27 L D.30 L
B
5.教材练习第2题变式题 为增加公民的节约用电意识,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(kW·h)之间的函数图象如图所示.
(1)求y与x之间的函数表达式;
(2)若乙用户某月需缴电费132元,求乙用户该月的用电量.
解:(1)当0≤x≤200时,设y=kx,则100=200k,解得k=0.5.
所以当0≤x≤200时,y=0.5x.当x>200时,设y=mx+b.
100=200m+b,
180=300m+b,
m=0.8,
b=-60,
所以当x>200时,y=0.8x-60.
综上可得,y与x之间的函数表达式是y=
0.5x(0≤x≤200),
0.8x-60(x>200),
(2)由图可知乙用户该月用电量超过200 kW·h,
将y=132代入y=0.8x-60,得x=240.
即乙用户该月的用电量是240 kW·h.
第十二章 一次函数
12.2 一次函数(第5课时)
情境导入
小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.
该图表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
获取新知
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12
14
16
18
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
解:设购买量为x千克,付款金额为y元.
当x>2时,
y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
∴y =
5x(0≤x≤2)
4x+2(x>2)
函数图象为:
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
例题精讲
例 为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过8立方米时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数关系式;
解:(1)y关于x的函数关系式为
(1+0.3)x =1.3x (0≤x≤8),
(1.5+1.2)(x-8)+1.3 × 8=2.7x-11.2 (x>8);
y=
函数图象如图所示;
30
20
10
8
16
O
.
.
(8,10.4)
(16,32)
y/元
x/m3
(2)画出上述函数图象;
(3)该市某户某月若用水x=5立
方米或x=10立方米时,
求应缴水费;
(3)当x=5 m3时,
y=1.3×5=6.5(元);
当x=10m3时,y=2.7×10-11.2=15.8(元).
即当用水量为5m3时,该户应缴水费6.5元;当用水量为10m3时,该户应缴水费15.8元.
(4)y=26.6>1.3×8,可知该户这月用水超过8m3,
因此,2.7x-11.2=26.6,
解方程,得 x=14.
即该户本月用水量为14m3.
(4)该市某户某月缴水费26.6元,求该户这月用水量.
要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程.
课堂小结
分段函数
对分段函数图像的理解
分段函数的具体应用
随堂演练
1.目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数表达式是( )
A.y=0.05x B.y=5x
C.y=100x D.y=0.05x+100
B
2.2018·和县期末一个有进水管与出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则8 min时容器内的水量为( )
A.20 L B.25 L C.27 L D.30 L
B
5.教材练习第2题变式题 为增加公民的节约用电意识,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(kW·h)之间的函数图象如图所示.
(1)求y与x之间的函数表达式;
(2)若乙用户某月需缴电费132元,求乙用户该月的用电量.
解:(1)当0≤x≤200时,设y=kx,则100=200k,解得k=0.5.
所以当0≤x≤200时,y=0.5x.当x>200时,设y=mx+b.
100=200m+b,
180=300m+b,
m=0.8,
b=-60,
所以当x>200时,y=0.8x-60.
综上可得,y与x之间的函数表达式是y=
0.5x(0≤x≤200),
0.8x-60(x>200),
(2)由图可知乙用户该月用电量超过200 kW·h,
将y=132代入y=0.8x-60,得x=240.
即乙用户该月的用电量是240 kW·h.
