沪科版数学八年级上册12.2一次函数(第4课时)同步课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级上册12.2一次函数(第4课时)同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 697.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第十二章 一次函数
12.2 一次函数(第4课时)
知识回顾
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
两点法——两点确定一条直线
思考:反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
获取新知
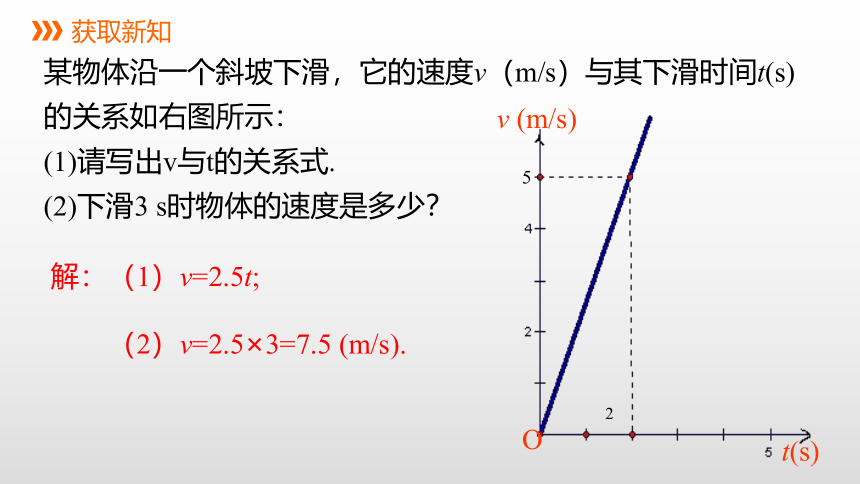
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如右图所示:
(1)请写出v与t的关系式.
(2)下滑3 s时物体的速度是多少?
v (m/s)
t(s)
O
5
2
解:(1)v=2.5t;
(2)v=2.5×3=7.5 (m/s).
想一想:确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
一个
两个
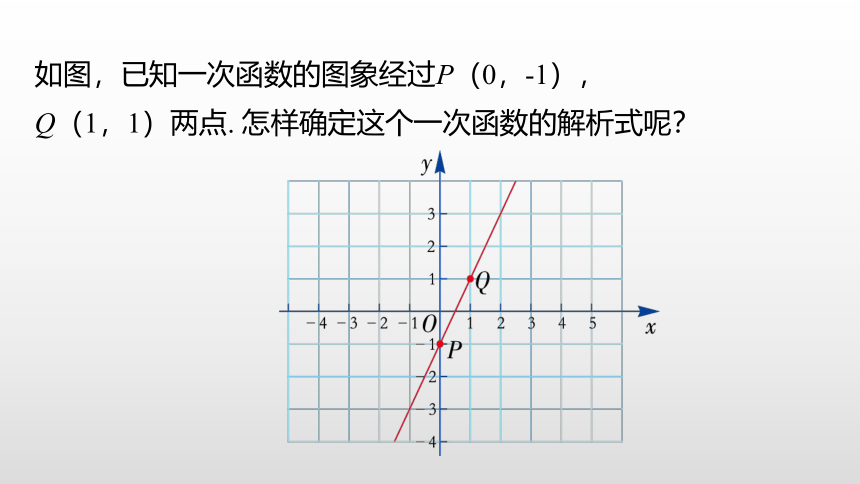
如图,已知一次函数的图象经过P(0,-1),
Q(1,1)两点. 怎样确定这个一次函数的解析式呢?
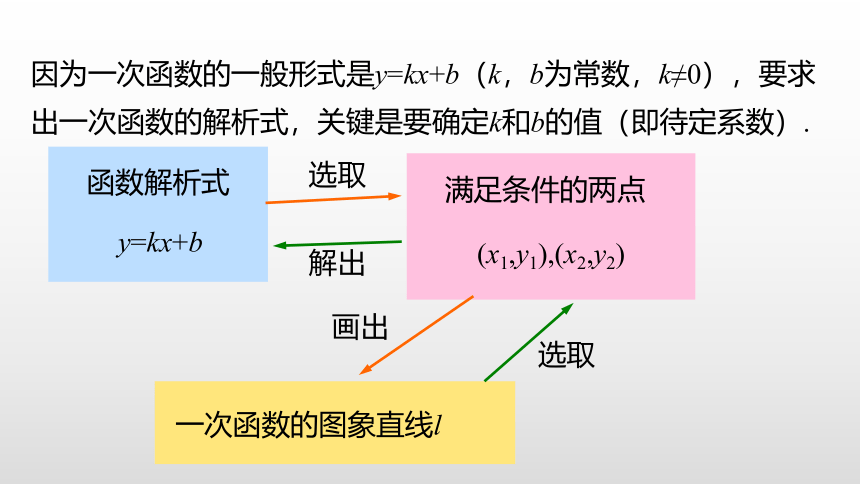
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象直线l
选取
解出
画出
选取
∵P(0,-1) 和Q(1,1)都在该函数图象上,
∴它们的坐标应满足y=kx+b , 将这两点坐标代入该式中,得到一个关于k,b的二元一次方程组:
k·0 + b = -1,
k + b = 1,
{
{
解这个方程组,得
k=2,
b=-1.
∴这个一次函数的解析式为y = 2x- 1.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
例 如果知道一个一次函数,当自变量x=4时,函数值y=5;当x=5时,y=2.你能画出它的图象,并写出函数解析式吗?
解:因为y是x的一次函数,设其表达式为y=kx+b.
由题意得 解得
4k+b=5,
5k+b=2,
所以,函数表达式为 y=-3x+17,
图象如图所示.
k=-3,
b=17,
例题精讲
课堂小结
利用二元一次方程组求一次函数表达式的一般步骤
1.用含字母的系数设出一次函数的表达式:y=kx+b.
2.将已知条件代入上述表达式中得k,b的二元一次方程组.
3.解这个二元一次方程组得k,b.
4.进而求出一次函数的表达式.
随堂演练
1.下表是一次函数的自变量x与函数值y的三组对应值,则一次函数的表达式为( )
x -2 1 2
y 3 0 -1
A. y=-x+1 B.y=-x-1
C.y=x-1 D.y=x+1
A
2.教材例4变式题 已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的表达式.
解:设这个一次函数的表达式为y=kx+b.
将x=3,y=1;x=-2,y=-4分别代入,得
3k+b=1,
-2k+b=-4,
k=1,
b=-2,
则这个一次函数的表达式为y=x-2.
10.2019·淮南谢家集区期末 已知一次函数的图象经过A(1,-2),B(3,2)两点.
(1)求这个一次函数的表达式;
(2)试判断点P(-1,-5)是否在这个一次函数的图象上;
(3)求此函数图象与x轴、y轴围成的三角形的面积.
解:(1)设一次函数的解析式为y=kx+b.
把A(1,-2),B(3,2)代入,得
k+b=-2,
3k+b=2,
k=2,
b=-4,
所以一次函数的解析式为y=2x-4.
(2)当x=-1时,
y=2x-4=-2-4=-6≠-5,
所以点P(-1,-5)不在这个一次函数的图象上.
(3)当x=0时,y=2x-4=-4,则一次函数图象与y轴的交点坐标为(0,-4).
当y=0时,2x-4=0,解得x=2,则一次函数图象与x轴的交点坐标为(2,0).
故此函数图象与x轴、y轴围成的三角形的面积为 ×2×4=4.
1
2
_____
4.如图,一次函数y=kx+k-3的图象经过点M,则一次函数的表达式为______________.
y=-4x-7
第十二章 一次函数
12.2 一次函数(第4课时)
知识回顾
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
两点法——两点确定一条直线
思考:反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
获取新知
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如右图所示:
(1)请写出v与t的关系式.
(2)下滑3 s时物体的速度是多少?
v (m/s)
t(s)
O
5
2
解:(1)v=2.5t;
(2)v=2.5×3=7.5 (m/s).
想一想:确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
一个
两个
如图,已知一次函数的图象经过P(0,-1),
Q(1,1)两点. 怎样确定这个一次函数的解析式呢?
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象直线l
选取
解出
画出
选取
∵P(0,-1) 和Q(1,1)都在该函数图象上,
∴它们的坐标应满足y=kx+b , 将这两点坐标代入该式中,得到一个关于k,b的二元一次方程组:
k·0 + b = -1,
k + b = 1,
{
{
解这个方程组,得
k=2,
b=-1.
∴这个一次函数的解析式为y = 2x- 1.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
例 如果知道一个一次函数,当自变量x=4时,函数值y=5;当x=5时,y=2.你能画出它的图象,并写出函数解析式吗?
解:因为y是x的一次函数,设其表达式为y=kx+b.
由题意得 解得
4k+b=5,
5k+b=2,
所以,函数表达式为 y=-3x+17,
图象如图所示.
k=-3,
b=17,
例题精讲
课堂小结
利用二元一次方程组求一次函数表达式的一般步骤
1.用含字母的系数设出一次函数的表达式:y=kx+b.
2.将已知条件代入上述表达式中得k,b的二元一次方程组.
3.解这个二元一次方程组得k,b.
4.进而求出一次函数的表达式.
随堂演练
1.下表是一次函数的自变量x与函数值y的三组对应值,则一次函数的表达式为( )
x -2 1 2
y 3 0 -1
A. y=-x+1 B.y=-x-1
C.y=x-1 D.y=x+1
A
2.教材例4变式题 已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的表达式.
解:设这个一次函数的表达式为y=kx+b.
将x=3,y=1;x=-2,y=-4分别代入,得
3k+b=1,
-2k+b=-4,
k=1,
b=-2,
则这个一次函数的表达式为y=x-2.
10.2019·淮南谢家集区期末 已知一次函数的图象经过A(1,-2),B(3,2)两点.
(1)求这个一次函数的表达式;
(2)试判断点P(-1,-5)是否在这个一次函数的图象上;
(3)求此函数图象与x轴、y轴围成的三角形的面积.
解:(1)设一次函数的解析式为y=kx+b.
把A(1,-2),B(3,2)代入,得
k+b=-2,
3k+b=2,
k=2,
b=-4,
所以一次函数的解析式为y=2x-4.
(2)当x=-1时,
y=2x-4=-2-4=-6≠-5,
所以点P(-1,-5)不在这个一次函数的图象上.
(3)当x=0时,y=2x-4=-4,则一次函数图象与y轴的交点坐标为(0,-4).
当y=0时,2x-4=0,解得x=2,则一次函数图象与x轴的交点坐标为(2,0).
故此函数图象与x轴、y轴围成的三角形的面积为 ×2×4=4.
1
2
_____
4.如图,一次函数y=kx+k-3的图象经过点M,则一次函数的表达式为______________.
y=-4x-7
