沪科版数学八年级上册13.2命题与证明(第3课时)同步课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级上册13.2命题与证明(第3课时)同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 15:16:23 | ||
图片预览




文档简介
(共16张PPT)
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明(第2课时)
新课导入
在证明命题时,要分清命题的条件和结论,如果问题与图形有关,首先画出图形,再结合图形,写出已知、求证.
命题:三角形的内角和等于180°.
你能证明这个命题吗?
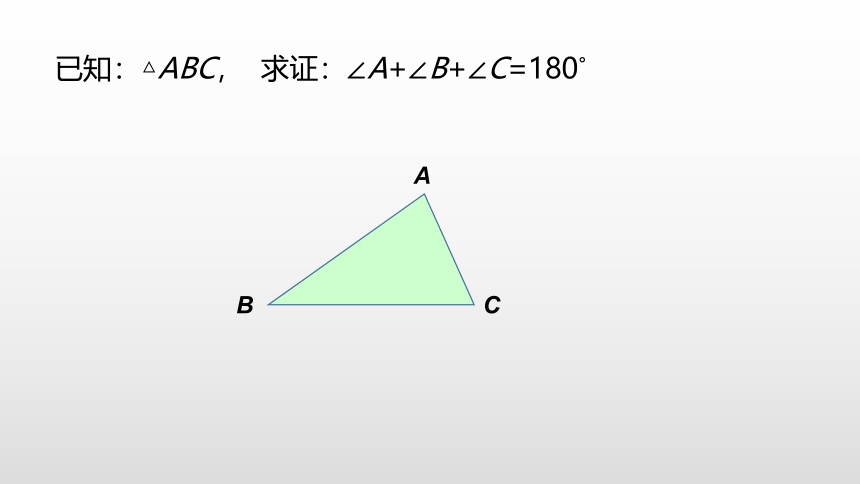
已知:△ABC, 求证:∠A+∠B+∠C=180°
A
B
C
获取新知
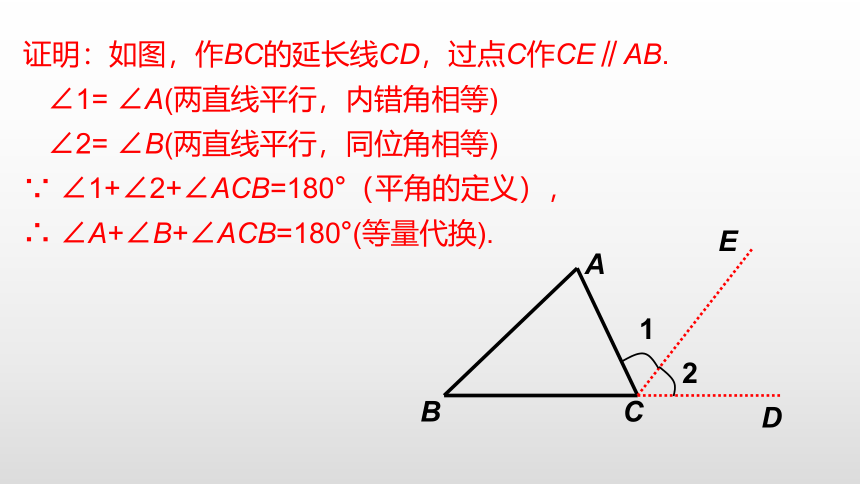
分析:以前我们通过剪拼将三角形的三个内角拼成了一个平角,这不是证明,但它却给我们以启发.现在我们通过作图来实现这种转化,给出证明.
A
B
C
1
2
D
E
证明:如图,作BC的延长线CD,过点C作CE∥AB.
∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B(两直线平行,同位角相等)
∵ ∠1+∠2+∠ACB=180°(平角的定义),
∴ ∠A+∠B+∠ACB=180°(等量代换).
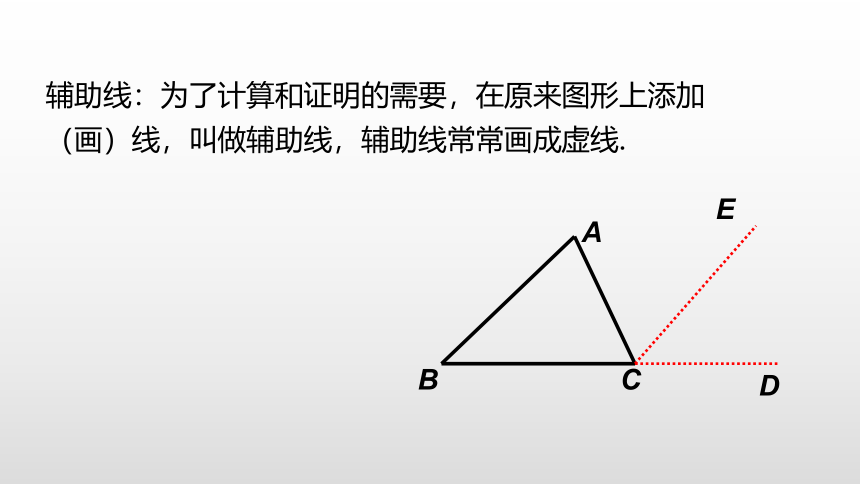
辅助线:为了计算和证明的需要,在原来图形上添加(画)线,叫做辅助线,辅助线常常画成虚线.
A
B
C
D
E
问题1:直角三角形中的两个锐角之间有着怎样的关系?
根据三角形内角和定理,另两个角的和应该为90°,于是得
推论1 直角三角形的两锐角互余.
像这样,由基本事实、定理直接得出的真命题叫做推论.
推论2 有两个角互余的三角形是直角三角形.
例题精讲
[教材补充例题] 如图,在△ABC中,∠ACB=90°,∠ACD=∠B,判断△ADC的形状.
解:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠ACD+∠A=90°.
∴∠ADC=180°-∠ACD-∠A=90°.
∴△ADC是直角三角形.
课堂小结
文字类证明题的一般步骤:
(1)审题.分清命题的条件与结论;
(2)画图.依照题意画出图形,并在图形上标出有关字母与符号.画图时要做到图形正确且具有一般性,切忌将图形特殊化;
(3)写出“已知”“求证”.按照图形,将“条件”与“结论”翻译成“已知”与“求证”;
(4)分析因果关系,找出证明途径;
(5)规范地写出证明过程.
(1)三角形内角和定理:三角形的内角和等于180°;
(2)推论1:直角三角形的两锐角互余;
(3)推论2:有两个角互余的三角形是直角三角形.
随堂演练
1.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,∠A=46°,∠1=52°,则∠2的度数为( )
A.92° B.94° C.96° D.98°
D
2.如图,AB,CD相交于点O,AC⊥CD于点C.若∠BOD=38°,则∠A=________°.
52
3.如图13-2-13,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD和△BCD是直角三角形.
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°.
∴∠ADC=180°-∠A-∠ACD=90°,
即△ACD是直角三角形.
∵∠ADC=90°,
∴∠BDC=90°.
∴△BCD是直角三角形.
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明(第2课时)
新课导入
在证明命题时,要分清命题的条件和结论,如果问题与图形有关,首先画出图形,再结合图形,写出已知、求证.
命题:三角形的内角和等于180°.
你能证明这个命题吗?
已知:△ABC, 求证:∠A+∠B+∠C=180°
A
B
C
获取新知
分析:以前我们通过剪拼将三角形的三个内角拼成了一个平角,这不是证明,但它却给我们以启发.现在我们通过作图来实现这种转化,给出证明.
A
B
C
1
2
D
E
证明:如图,作BC的延长线CD,过点C作CE∥AB.
∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B(两直线平行,同位角相等)
∵ ∠1+∠2+∠ACB=180°(平角的定义),
∴ ∠A+∠B+∠ACB=180°(等量代换).
辅助线:为了计算和证明的需要,在原来图形上添加(画)线,叫做辅助线,辅助线常常画成虚线.
A
B
C
D
E
问题1:直角三角形中的两个锐角之间有着怎样的关系?
根据三角形内角和定理,另两个角的和应该为90°,于是得
推论1 直角三角形的两锐角互余.
像这样,由基本事实、定理直接得出的真命题叫做推论.
推论2 有两个角互余的三角形是直角三角形.
例题精讲
[教材补充例题] 如图,在△ABC中,∠ACB=90°,∠ACD=∠B,判断△ADC的形状.
解:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠ACD+∠A=90°.
∴∠ADC=180°-∠ACD-∠A=90°.
∴△ADC是直角三角形.
课堂小结
文字类证明题的一般步骤:
(1)审题.分清命题的条件与结论;
(2)画图.依照题意画出图形,并在图形上标出有关字母与符号.画图时要做到图形正确且具有一般性,切忌将图形特殊化;
(3)写出“已知”“求证”.按照图形,将“条件”与“结论”翻译成“已知”与“求证”;
(4)分析因果关系,找出证明途径;
(5)规范地写出证明过程.
(1)三角形内角和定理:三角形的内角和等于180°;
(2)推论1:直角三角形的两锐角互余;
(3)推论2:有两个角互余的三角形是直角三角形.
随堂演练
1.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,∠A=46°,∠1=52°,则∠2的度数为( )
A.92° B.94° C.96° D.98°
D
2.如图,AB,CD相交于点O,AC⊥CD于点C.若∠BOD=38°,则∠A=________°.
52
3.如图13-2-13,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD和△BCD是直角三角形.
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°.
∴∠ADC=180°-∠A-∠ACD=90°,
即△ACD是直角三角形.
∵∠ADC=90°,
∴∠BDC=90°.
∴△BCD是直角三角形.
