沪科版数学八年级上册14.2三角形全等的判定(第4课时)同步课件(共11张PPT)
文档属性
| 名称 | 沪科版数学八年级上册14.2三角形全等的判定(第4课时)同步课件(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 15:25:40 | ||
图片预览



文档简介
(共11张PPT)
第十四章 全等三角形
14.2 三角形全等的判定(第4课时)
知识回顾
(2)哪位同学来总结一下证明三角形全等的方法?
方法1:边角边(SAS)
方法2:角边角(ASA)
方法3:边边边(SSS)
(1)三角形中已知三个元素,包括哪几种情况?
三个角、三个边、两边一角、两角一边
获取新知
想一想,分别满足后面三组条件中任一组的两个三角形,即
(1)三个角分别相等;
(2)两边和其中一边的对角分别相等;
(3)两角和其中一角的对边分别相等;
能判定这两个三角形全等吗
(1)(2)不全等,(3)不全等
提示:举个例子进行反驳
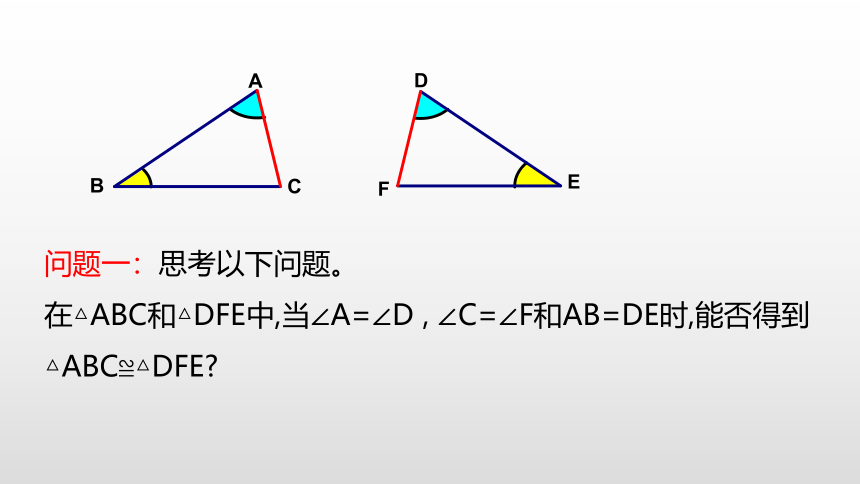
问题一:思考以下问题。
在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE
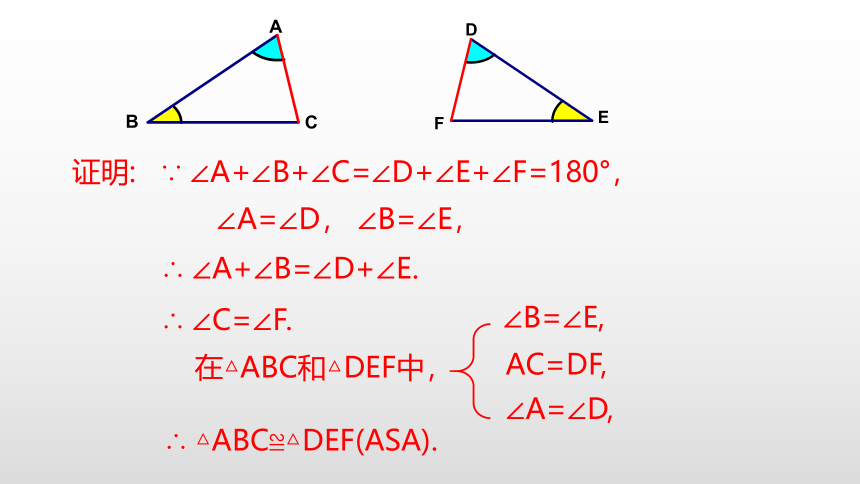
证明: ∵ ∠A+∠B+∠C=∠D+∠E+∠F=180°,
∠A=∠D, ∠B=∠E,
∴ ∠A+∠B=∠D+∠E.
∴ ∠C=∠F.
∴ △ABC≌△DEF(ASA).
在△ABC和△DEF中,
∠B=∠E,
AC=DF,
∠A=∠D,
三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角边角”或“AAS”)。
用符号语言表达为:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(AAS)
∠A=∠D
∠B=∠E
CA=FD
要注意这里的边是其中一角的对边,要注意区分!
例题精讲
例6 如图,点B、F、C、D在一条直线上,AB=ED, AB∥ED, AC∥EF求证:△ABC≌△EDF.
E
D
C
F
B
A
证明:∵ AB∥ED, AC∥EF
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
课堂小结
1全等三角形的判定4--AAS
2由全等证明边相等,角相等
随堂演练
1.如图所示,在△ABC和△ABC′中,AB=AB,AC=AC′,∠ABC=∠ABC′,但显然△ABC与△ABC′不全等,这说明当两个三角形有________________________相等时,这两个三角形不一定全等.
两边和其中一边的对角
2.如图,AD平分∠BAC,∠B=∠C=90°,则判定△ABD和△ACD全等的直接依据是______________.
AAS
3.2019·益阳 如图所示,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
证明:由∠ECB=70°得∠ACB=110°.
又∵∠D=110°,∴∠ACB=∠D.
∵AB∥DE,∴∠CAB=∠E.
在△ABC和△EAD中,
∵
∠ACB=∠D,
∠CAB=∠E,
AB=AE,
∴△ABC≌△EAD.(AAS)
第十四章 全等三角形
14.2 三角形全等的判定(第4课时)
知识回顾
(2)哪位同学来总结一下证明三角形全等的方法?
方法1:边角边(SAS)
方法2:角边角(ASA)
方法3:边边边(SSS)
(1)三角形中已知三个元素,包括哪几种情况?
三个角、三个边、两边一角、两角一边
获取新知
想一想,分别满足后面三组条件中任一组的两个三角形,即
(1)三个角分别相等;
(2)两边和其中一边的对角分别相等;
(3)两角和其中一角的对边分别相等;
能判定这两个三角形全等吗
(1)(2)不全等,(3)不全等
提示:举个例子进行反驳
问题一:思考以下问题。
在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE
证明: ∵ ∠A+∠B+∠C=∠D+∠E+∠F=180°,
∠A=∠D, ∠B=∠E,
∴ ∠A+∠B=∠D+∠E.
∴ ∠C=∠F.
∴ △ABC≌△DEF(ASA).
在△ABC和△DEF中,
∠B=∠E,
AC=DF,
∠A=∠D,
三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角边角”或“AAS”)。
用符号语言表达为:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(AAS)
∠A=∠D
∠B=∠E
CA=FD
要注意这里的边是其中一角的对边,要注意区分!
例题精讲
例6 如图,点B、F、C、D在一条直线上,AB=ED, AB∥ED, AC∥EF求证:△ABC≌△EDF.
E
D
C
F
B
A
证明:∵ AB∥ED, AC∥EF
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
课堂小结
1全等三角形的判定4--AAS
2由全等证明边相等,角相等
随堂演练
1.如图所示,在△ABC和△ABC′中,AB=AB,AC=AC′,∠ABC=∠ABC′,但显然△ABC与△ABC′不全等,这说明当两个三角形有________________________相等时,这两个三角形不一定全等.
两边和其中一边的对角
2.如图,AD平分∠BAC,∠B=∠C=90°,则判定△ABD和△ACD全等的直接依据是______________.
AAS
3.2019·益阳 如图所示,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
证明:由∠ECB=70°得∠ACB=110°.
又∵∠D=110°,∴∠ACB=∠D.
∵AB∥DE,∴∠CAB=∠E.
在△ABC和△EAD中,
∵
∠ACB=∠D,
∠CAB=∠E,
AB=AE,
∴△ABC≌△EAD.(AAS)
