沪科版数学八年级上册14.2三角形全等的判定(第5课时)同步课件(共14张PPT)
文档属性
| 名称 | 沪科版数学八年级上册14.2三角形全等的判定(第5课时)同步课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 272.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第十四章 全等三角形
14.2 三角形全等的判定(第5课时)
知识回顾
哪位同学来总结一下证明三角形全等的方法?
方法1:边角边(SAS)
方法2:角边角(ASA)
方法3:边边边(SSS)
方法4:角角边(AAS)
获取新知
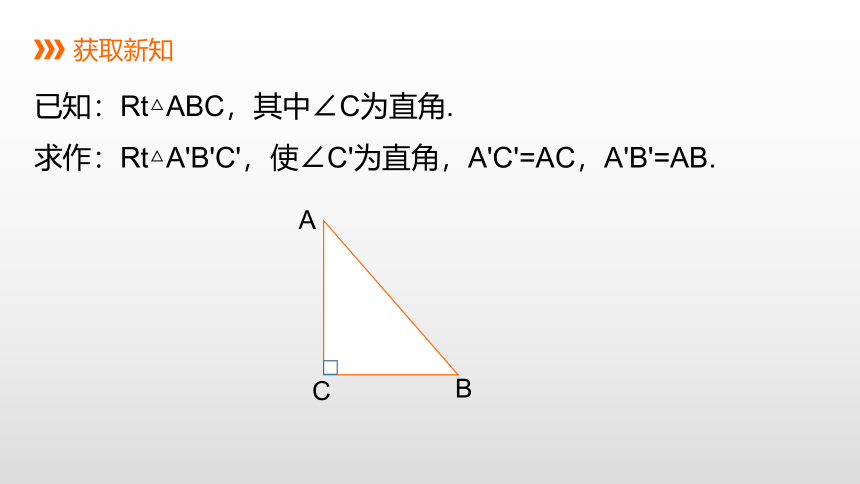
已知:Rt△ABC,其中∠C为直角.
求作:Rt△A'B'C',使∠C'为直角,A'C'=AC,A'B'=AB.
A
B
C
作法:
(1)作∠MC'N=∠C=90°;
(2)在C'M上截取C'A'=CA;
(3)以A'为圆心、AB长为半径画弧,交C'N于点B';
(4)连接A'B'.
则Rt△A'B'C'就是所求作的直角三角形.
A'
B'
C'
M
N
A
B
C
A'
B'
C'
M
N
将画好的Rt△A‘B’C‘与Rt△ABC叠一叠,看看它们能否完全重合?由此你能得到什么结论?
斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL”.
例题精讲
例7 已知:如图∠BAC=∠CDB=90°,AC=DB,求证:AB=DC.
证明 ∵∠BAC=∠CDB=90°(已知)
∴△BAC,△CDB都是直角三角形
又∵AC=DB(已知)
BC=CB(公共边)
∴Rt△ABC≌Rt△DCB(HL)
∴AB=DC(全等三角形的对应边相等)
例8 已知:如图AB=CD,BC=DA,E,F是AC上的两点,
且AE=CF.求证:BF=DE.
分析 :
本题需要两次证明三角形全等,
首先证明△ABC≌△CDA(SSS),
得出∠1=∠2,
再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
证明 在△ABC和△CDA中
AB=CD(已知)
∵ BC=DA(已知)
CA=AC(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA(已知)
∵ ∠1=∠2(已证)
CF=AE(已知)
∴△BCF≌△DAE(SAS)
∴BF=DE(全等三角形的对应边相等)
课堂小结
判定直角三角形全等的“四种思路”:
(1)若有一组直角边和斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等:①直角边是锐角的对边,用“AAS”判定;②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
随堂演练
1.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA C.SSA D.HL
D
2.教材练习第1题变式题 如图,已知CE⊥AB,DF⊥AB,垂足分别为E,F,AC=BD,CE=DF.求证:AC∥BD.
证明:∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
在Rt△ACE和Rt△BDF中,
∵
AC=BD,
CE=DF
∴Rt△ACE≌Rt△BDF.(HL)
∴∠A=∠B. ∴AC∥BD.
3.你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直.当一方着地时,另一方上升到最高点.根据________判定△AA′B≌△BB′A,所以AA′=________.
HL
BB′
第十四章 全等三角形
14.2 三角形全等的判定(第5课时)
知识回顾
哪位同学来总结一下证明三角形全等的方法?
方法1:边角边(SAS)
方法2:角边角(ASA)
方法3:边边边(SSS)
方法4:角角边(AAS)
获取新知
已知:Rt△ABC,其中∠C为直角.
求作:Rt△A'B'C',使∠C'为直角,A'C'=AC,A'B'=AB.
A
B
C
作法:
(1)作∠MC'N=∠C=90°;
(2)在C'M上截取C'A'=CA;
(3)以A'为圆心、AB长为半径画弧,交C'N于点B';
(4)连接A'B'.
则Rt△A'B'C'就是所求作的直角三角形.
A'
B'
C'
M
N
A
B
C
A'
B'
C'
M
N
将画好的Rt△A‘B’C‘与Rt△ABC叠一叠,看看它们能否完全重合?由此你能得到什么结论?
斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL”.
例题精讲
例7 已知:如图∠BAC=∠CDB=90°,AC=DB,求证:AB=DC.
证明 ∵∠BAC=∠CDB=90°(已知)
∴△BAC,△CDB都是直角三角形
又∵AC=DB(已知)
BC=CB(公共边)
∴Rt△ABC≌Rt△DCB(HL)
∴AB=DC(全等三角形的对应边相等)
例8 已知:如图AB=CD,BC=DA,E,F是AC上的两点,
且AE=CF.求证:BF=DE.
分析 :
本题需要两次证明三角形全等,
首先证明△ABC≌△CDA(SSS),
得出∠1=∠2,
再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
证明 在△ABC和△CDA中
AB=CD(已知)
∵ BC=DA(已知)
CA=AC(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA(已知)
∵ ∠1=∠2(已证)
CF=AE(已知)
∴△BCF≌△DAE(SAS)
∴BF=DE(全等三角形的对应边相等)
课堂小结
判定直角三角形全等的“四种思路”:
(1)若有一组直角边和斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等:①直角边是锐角的对边,用“AAS”判定;②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
随堂演练
1.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA C.SSA D.HL
D
2.教材练习第1题变式题 如图,已知CE⊥AB,DF⊥AB,垂足分别为E,F,AC=BD,CE=DF.求证:AC∥BD.
证明:∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
在Rt△ACE和Rt△BDF中,
∵
AC=BD,
CE=DF
∴Rt△ACE≌Rt△BDF.(HL)
∴∠A=∠B. ∴AC∥BD.
3.你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直.当一方着地时,另一方上升到最高点.根据________判定△AA′B≌△BB′A,所以AA′=________.
HL
BB′
