沪科版数学八年级上册15.1轴对称图形(第3课时)同步课件(共11张PPT)
文档属性
| 名称 | 沪科版数学八年级上册15.1轴对称图形(第3课时)同步课件(共11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
第十五章 轴对称图形与等腰三角形
15.1 轴对称图形(第3课时)
知识回顾
1:轴对称图形
2:轴对称
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形.这条直线叫做对称轴.
如果平面内两个图形沿着一条直线对折后,它们能完全重合,那么称这两个图形成轴对称,这条直线就是对称轴.
获取新知
思考:如图,△ABC与△A‘B’C’,关于直线l对称,点A’,B’,C’分别是店A,B,C的对应点.连接AA‘,设AA’与直线l交于点O1.
(1)直线l与线段AA‘有怎样的位置关系?
(2)O1A与O1A’的长度有何关系?
A
A’
l
B
B’
C
C’
O1
O2
O3
A
A’
l
B
B’
C
C’
O1
O2
O3
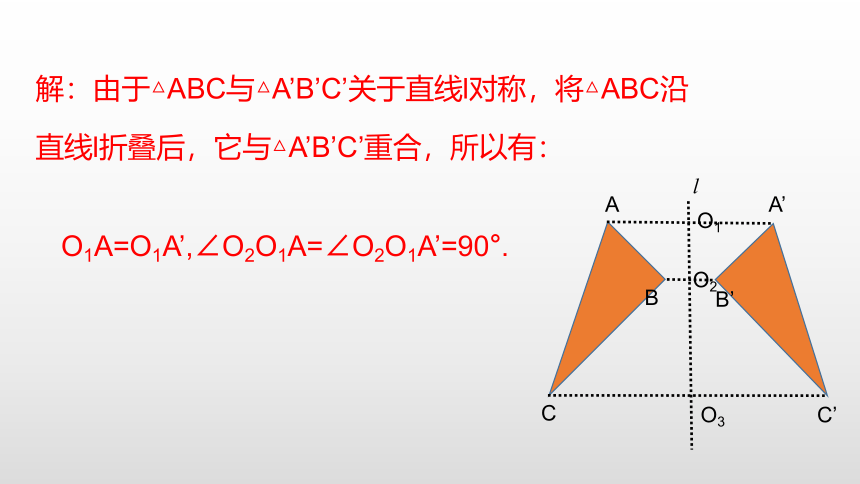
解:由于△ABC与△A’B’C’关于直线l对称,将△ABC沿直线l折叠后,它与△A’B’C’重合,所以有:
O1A=O1A’,∠O2O1A=∠O2O1A’=90°.
经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线,又叫做线段的中垂线.
一般地,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连接线段的垂直平分线;反过来,成轴对称图形的两个图形中,对应点的连线被对称轴垂直平分.
例题精讲
[教材补充例题] 在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是( , ).
[解析] 点A (2,-3) 关于x轴的对称点A'的坐标是(2,3),点A'(2,3) 关于y轴的对称点A″的坐标是(-2,3).
-2
3
[教材补充例题] 如图,分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2,并写出变换后图形各顶点的坐标.
解:如图所示.
△A1B1C1是
△ABC关于x轴对称的图形,其中A1(0,2),B1(2,4),C1(4,1);
△A2B2C2是
△ABC关于y轴对称的图形,
其中A2(0,-2),B2(-2,-4),C2(-4,-1).
随堂演练
1.如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( )
A.(-4,6) B.(4,6)
C.(-2,1) D.(6,2)
B
2.已知点A(2m+n,2),B(1,n-m),当m,n分别为何值时,满足点A,B关于x轴对称
解:由题意,得
2m+n=1
m-n=2
解得
m=1
n=-1
即当m=1,n=-1时,点A,B关于x轴对称.
3.教材练习第2题变式题 △ABC在平面直角坐标系中的位置如图所示.
(1)作出与△ABC关于y轴对称的△A1B1C1;
(2)作出与△ABC关于x轴对称的△A2B2C2.
解:(1)(2)如图所示:
第十五章 轴对称图形与等腰三角形
15.1 轴对称图形(第3课时)
知识回顾
1:轴对称图形
2:轴对称
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形.这条直线叫做对称轴.
如果平面内两个图形沿着一条直线对折后,它们能完全重合,那么称这两个图形成轴对称,这条直线就是对称轴.
获取新知
思考:如图,△ABC与△A‘B’C’,关于直线l对称,点A’,B’,C’分别是店A,B,C的对应点.连接AA‘,设AA’与直线l交于点O1.
(1)直线l与线段AA‘有怎样的位置关系?
(2)O1A与O1A’的长度有何关系?
A
A’
l
B
B’
C
C’
O1
O2
O3
A
A’
l
B
B’
C
C’
O1
O2
O3
解:由于△ABC与△A’B’C’关于直线l对称,将△ABC沿直线l折叠后,它与△A’B’C’重合,所以有:
O1A=O1A’,∠O2O1A=∠O2O1A’=90°.
经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线,又叫做线段的中垂线.
一般地,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连接线段的垂直平分线;反过来,成轴对称图形的两个图形中,对应点的连线被对称轴垂直平分.
例题精讲
[教材补充例题] 在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是( , ).
[解析] 点A (2,-3) 关于x轴的对称点A'的坐标是(2,3),点A'(2,3) 关于y轴的对称点A″的坐标是(-2,3).
-2
3
[教材补充例题] 如图,分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2,并写出变换后图形各顶点的坐标.
解:如图所示.
△A1B1C1是
△ABC关于x轴对称的图形,其中A1(0,2),B1(2,4),C1(4,1);
△A2B2C2是
△ABC关于y轴对称的图形,
其中A2(0,-2),B2(-2,-4),C2(-4,-1).
随堂演练
1.如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( )
A.(-4,6) B.(4,6)
C.(-2,1) D.(6,2)
B
2.已知点A(2m+n,2),B(1,n-m),当m,n分别为何值时,满足点A,B关于x轴对称
解:由题意,得
2m+n=1
m-n=2
解得
m=1
n=-1
即当m=1,n=-1时,点A,B关于x轴对称.
3.教材练习第2题变式题 △ABC在平面直角坐标系中的位置如图所示.
(1)作出与△ABC关于y轴对称的△A1B1C1;
(2)作出与△ABC关于x轴对称的△A2B2C2.
解:(1)(2)如图所示:
