沪科版数学八年级上册15.3等腰三角形(第1课时)同步课件(共13张PPT)
文档属性
| 名称 | 沪科版数学八年级上册15.3等腰三角形(第1课时)同步课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 15:37:54 | ||
图片预览




文档简介
(共13张PPT)
第十五章 轴对称图形与等腰三角形
15.3 等腰三角形(第1课时)
情境导入
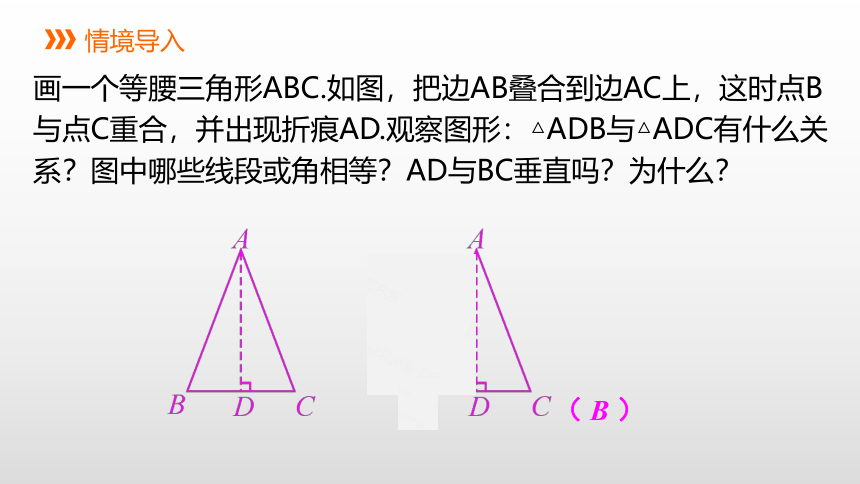
画一个等腰三角形ABC.如图,把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
( B )
获取新知
等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴.
由上面的操作,我们可以得到等腰三角形的如下性质:
定理1:等腰三角形两个底角相等,简称“等边对等角”.
等腰三角形性质定理1的内容如何证明?
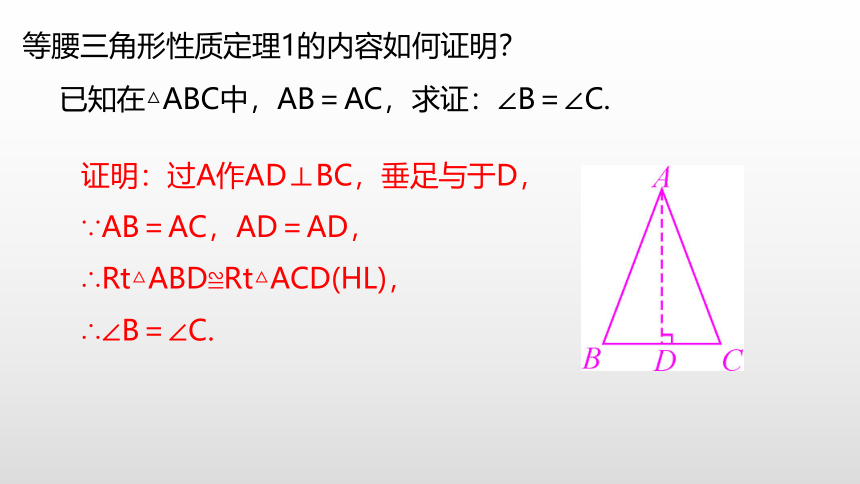
已知在△ABC中,AB=AC,求证:∠B=∠C.
证明:过A作AD⊥BC,垂足与于D,
∵AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴∠B=∠C.
由上面的证明可得,BD=DC,∠BAD=∠CAD,∠ADB=∠ADC=90°
因此有如下的性质:
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角平分线、底边上的中线和底边上的高线“三线合一”.
推论:等边三角形三个内角相等,每一个内角都等于60°.
例题精讲
例1 如图所示,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,
∴∠B=∠C.
∴∠B=∠C= ×(180°-120°)=30°.
又∵BD=AD,
∴∠BAD=∠B=30°.
同理,∠CAE=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°
[教材补充例题] 如图所示,已知点D,E在△ABC的边BC上,
AB=AC,AD=AE.求证:BD=CE.
证明:过点A作AF⊥BC,垂足为F.
因为AB=AC,AD=AE,AF⊥BC,
所以BF=CF,DF=EF.
所以BF-DF=CF-EF,
即BD=CE.
课堂小结
等腰三角形
定理1:等腰三角形两个底角相等,简称“等边对等角”.
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角平分线、底边上的中线和底边上的高线“三线合一”.
推论:等边三角形三个内角相等,每一个内角都等于60°.
随堂演练
1.如图,在等腰三角形ABC中,AB=AC,由于等腰三角形是轴对称图形,若其底角∠B=35°,则∠C=________°.
35
2.如图,在△ABC中,AB=AC,AD⊥BC,以下结论错误的是( )
A.△ABD≌△ACD B.∠B=∠BAD
C.D为BC的中点 D.AD是△ABC的角平分线
B
3.如图,在等边三角形ABC中,BD是△ABC的角平分线,延长BC到点E,使CE=CD,AB=6 cm.
求:(1)∠E的度数;
(2)BE的长.
解:(1)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E= ∠ACB=30°.
(2)∵△ABC是等边三角形,BD是△ABC的角平分线,
∴AB=AC=BC,D是AC的中点.
又∵AB=6 cm,
∴CD=3 cm,
∴BE=BC+CE=6+3=9(cm).
第十五章 轴对称图形与等腰三角形
15.3 等腰三角形(第1课时)
情境导入
画一个等腰三角形ABC.如图,把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
( B )
获取新知
等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴.
由上面的操作,我们可以得到等腰三角形的如下性质:
定理1:等腰三角形两个底角相等,简称“等边对等角”.
等腰三角形性质定理1的内容如何证明?
已知在△ABC中,AB=AC,求证:∠B=∠C.
证明:过A作AD⊥BC,垂足与于D,
∵AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴∠B=∠C.
由上面的证明可得,BD=DC,∠BAD=∠CAD,∠ADB=∠ADC=90°
因此有如下的性质:
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角平分线、底边上的中线和底边上的高线“三线合一”.
推论:等边三角形三个内角相等,每一个内角都等于60°.
例题精讲
例1 如图所示,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,
∴∠B=∠C.
∴∠B=∠C= ×(180°-120°)=30°.
又∵BD=AD,
∴∠BAD=∠B=30°.
同理,∠CAE=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°
[教材补充例题] 如图所示,已知点D,E在△ABC的边BC上,
AB=AC,AD=AE.求证:BD=CE.
证明:过点A作AF⊥BC,垂足为F.
因为AB=AC,AD=AE,AF⊥BC,
所以BF=CF,DF=EF.
所以BF-DF=CF-EF,
即BD=CE.
课堂小结
等腰三角形
定理1:等腰三角形两个底角相等,简称“等边对等角”.
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角平分线、底边上的中线和底边上的高线“三线合一”.
推论:等边三角形三个内角相等,每一个内角都等于60°.
随堂演练
1.如图,在等腰三角形ABC中,AB=AC,由于等腰三角形是轴对称图形,若其底角∠B=35°,则∠C=________°.
35
2.如图,在△ABC中,AB=AC,AD⊥BC,以下结论错误的是( )
A.△ABD≌△ACD B.∠B=∠BAD
C.D为BC的中点 D.AD是△ABC的角平分线
B
3.如图,在等边三角形ABC中,BD是△ABC的角平分线,延长BC到点E,使CE=CD,AB=6 cm.
求:(1)∠E的度数;
(2)BE的长.
解:(1)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E= ∠ACB=30°.
(2)∵△ABC是等边三角形,BD是△ABC的角平分线,
∴AB=AC=BC,D是AC的中点.
又∵AB=6 cm,
∴CD=3 cm,
∴BE=BC+CE=6+3=9(cm).
