沪科版数学八年级上册15.3等腰三角形(第2课时)同步课件(共13张PPT)
文档属性
| 名称 | 沪科版数学八年级上册15.3等腰三角形(第2课时)同步课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 15:41:51 | ||
图片预览



文档简介
(共13张PPT)
第十五章 轴对称图形与等腰三角形
15.3 等腰三角形(第2课时)
知识回顾
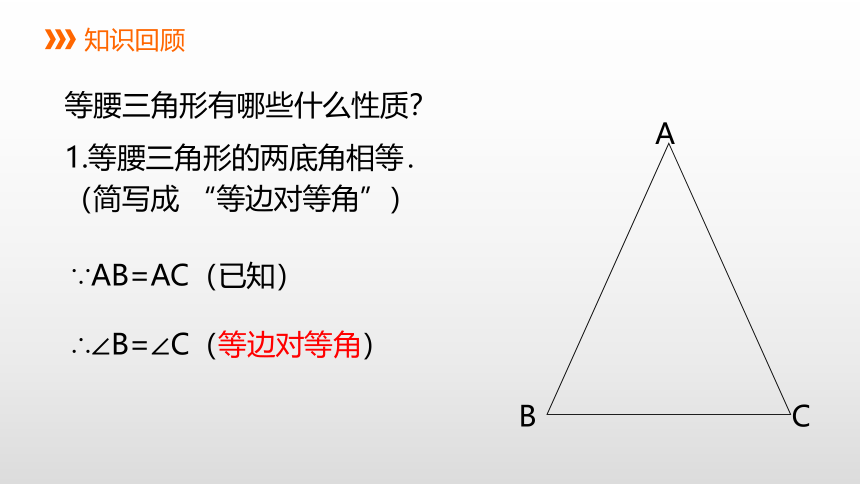
等腰三角形有哪些什么性质?
1.等腰三角形的两底角相等.
(简写成 “等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
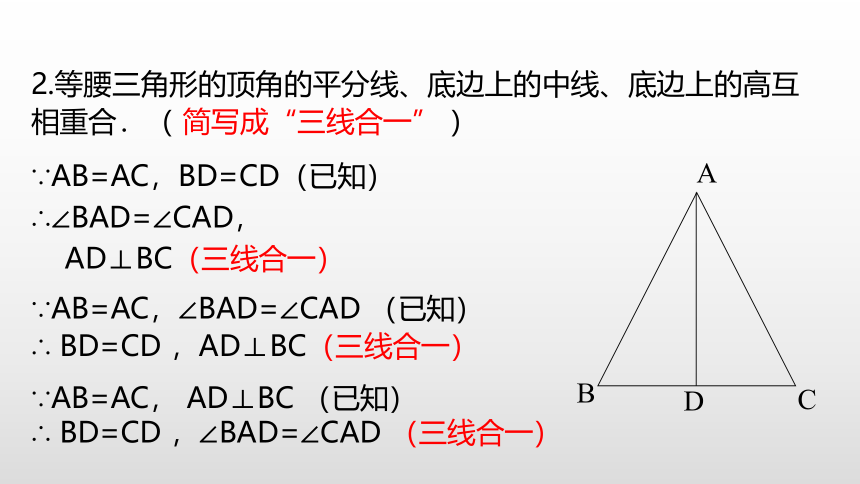
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
新知讲解
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”)
应用: 常用来证明线段相等和角相等,求等腰三角形各角的度数,可以设未知数,借助方程来解。
例题精讲
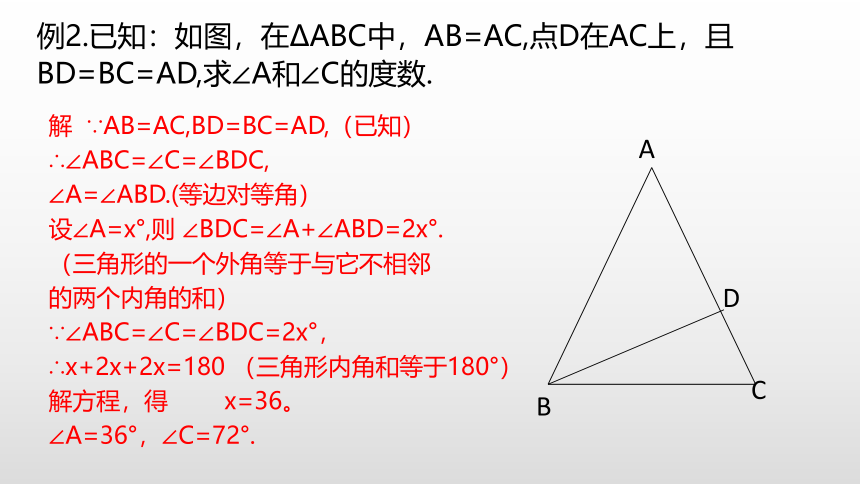
例2.已知:如图,在ΔABC中,AB=AC,点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
C
D
B
A
解 ∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,则 ∠BDC=∠A+∠ABD=2x°.
(三角形的一个外角等于与它不相邻
的两个内角的和)
∵∠ABC=∠C=∠BDC=2x°,
∴x+2x+2x=180 (三角形内角和等于180°)
解方程,得 x=36。
∠A=36°,∠C=72°.
活动探究:同学们,请回忆一下,回答下列问题。
1、咱们学过的判定三角形全等的方法有哪些呢?动手写一写。
(SSS)、(SAS)、(ASA)、(AAS)、( HL )
2、怎样证明两个直角三角形全等的定理“HL”?
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(简写成“三线和一”)
应用: 研究等腰三角形的有关问题时“三线”是常用的辅助线.
例3 求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在RtΔABC和RtΔA‘B’C‘中,∠C=∠C’=90°,AB=A‘B’,AC=A‘C’. 求证:RtΔABC≌RtΔA'B'C'.
C'
A'
C
B
A
(1)
B'
B'
C(C')
A(A')
(2)
B
证明 在平面内移动RtΔABC和RtΔA'B'C',
使点A和点A'、点C和点C'重合,点B和点B'在AC的两侧.
∵∠BCB'=90°+90°=180°,(等式性质)
∴B,C,B'三点在一条直线上.(平角定义)
在ΔABB'中,
∵AB=AB',(已知)
∴∠B=∠B'.(等边对等角)
在RtΔABC和RtΔA'B'C'中,
∠ACB=∠A'C'B',(已知)
∵ ∠B=∠B'(已证)
AB=A'B',(已知)
∴RtΔABC≌RtΔA'B'C'.(AAS)
B'
C(C')
A(A')
(2)
B
课堂小结
等 腰 三 角 形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”)
应用: 常用来证明线段相等和角相等,求等腰三角形各角的度数,可以设未知数,借助方程来解。
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 (简写成“三线和一”)
应用: 研究等腰三角形的有关问题时“三线”是常用的辅助线.
随堂演练
1.2019·衢州 “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A.60° B.65° C.75° D.80°
D
2.2019·重庆 如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠C=42°,
∴∠BAD=∠CAD=90°-42°=48°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AC,∴∠F=∠CAD,
∴∠BAD=∠F,∴AE=FE.
第十五章 轴对称图形与等腰三角形
15.3 等腰三角形(第2课时)
知识回顾
等腰三角形有哪些什么性质?
1.等腰三角形的两底角相等.
(简写成 “等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
新知讲解
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”)
应用: 常用来证明线段相等和角相等,求等腰三角形各角的度数,可以设未知数,借助方程来解。
例题精讲
例2.已知:如图,在ΔABC中,AB=AC,点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
C
D
B
A
解 ∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,则 ∠BDC=∠A+∠ABD=2x°.
(三角形的一个外角等于与它不相邻
的两个内角的和)
∵∠ABC=∠C=∠BDC=2x°,
∴x+2x+2x=180 (三角形内角和等于180°)
解方程,得 x=36。
∠A=36°,∠C=72°.
活动探究:同学们,请回忆一下,回答下列问题。
1、咱们学过的判定三角形全等的方法有哪些呢?动手写一写。
(SSS)、(SAS)、(ASA)、(AAS)、( HL )
2、怎样证明两个直角三角形全等的定理“HL”?
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(简写成“三线和一”)
应用: 研究等腰三角形的有关问题时“三线”是常用的辅助线.
例3 求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在RtΔABC和RtΔA‘B’C‘中,∠C=∠C’=90°,AB=A‘B’,AC=A‘C’. 求证:RtΔABC≌RtΔA'B'C'.
C'
A'
C
B
A
(1)
B'
B'
C(C')
A(A')
(2)
B
证明 在平面内移动RtΔABC和RtΔA'B'C',
使点A和点A'、点C和点C'重合,点B和点B'在AC的两侧.
∵∠BCB'=90°+90°=180°,(等式性质)
∴B,C,B'三点在一条直线上.(平角定义)
在ΔABB'中,
∵AB=AB',(已知)
∴∠B=∠B'.(等边对等角)
在RtΔABC和RtΔA'B'C'中,
∠ACB=∠A'C'B',(已知)
∵ ∠B=∠B'(已证)
AB=A'B',(已知)
∴RtΔABC≌RtΔA'B'C'.(AAS)
B'
C(C')
A(A')
(2)
B
课堂小结
等 腰 三 角 形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”)
应用: 常用来证明线段相等和角相等,求等腰三角形各角的度数,可以设未知数,借助方程来解。
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 (简写成“三线和一”)
应用: 研究等腰三角形的有关问题时“三线”是常用的辅助线.
随堂演练
1.2019·衢州 “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A.60° B.65° C.75° D.80°
D
2.2019·重庆 如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠C=42°,
∴∠BAD=∠CAD=90°-42°=48°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AC,∴∠F=∠CAD,
∴∠BAD=∠F,∴AE=FE.
