沪科版数学八年级上册15.4角的平分线(第1课时)同步课件(共13张PPT)
文档属性
| 名称 | 沪科版数学八年级上册15.4角的平分线(第1课时)同步课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 246.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
第十五章 轴对称图形与等腰三角形
15.4 角的平分线(第1课时)
知识导入
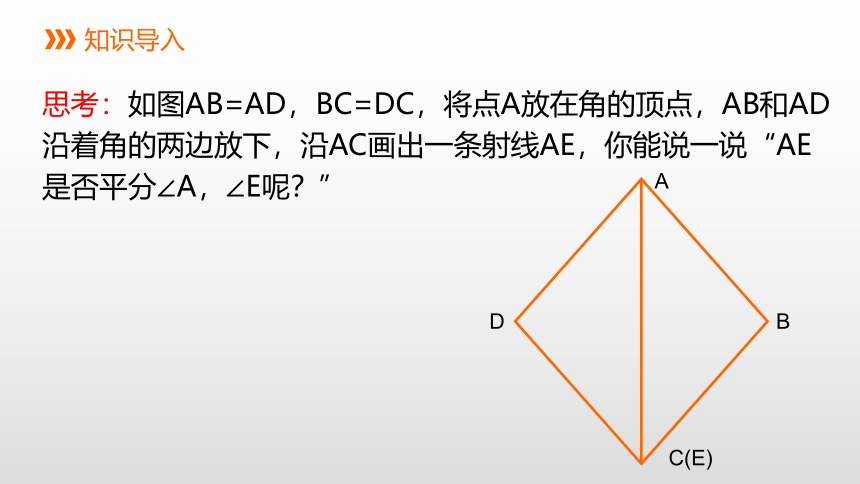
思考:如图AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画出一条射线AE,你能说一说“AE是否平分∠A,∠E呢?”
A
B
D
C(E)
新知讲解
怎样作出角的平分线?
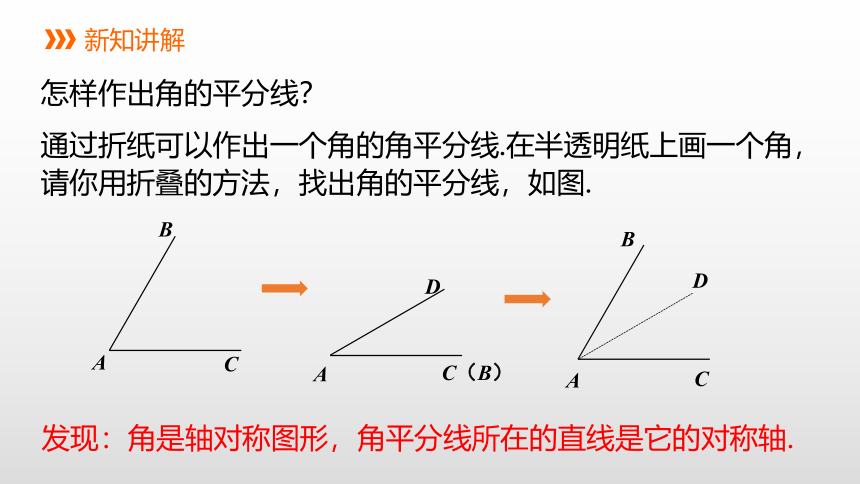
通过折纸可以作出一个角的角平分线.在半透明纸上画一个角,请你用折叠的方法,找出角的平分线,如图.
B
A
C
A
D
C(B)
A
D
C
B
发现:角是轴对称图形,角平分线所在的直线是它的对称轴.
尺规作图
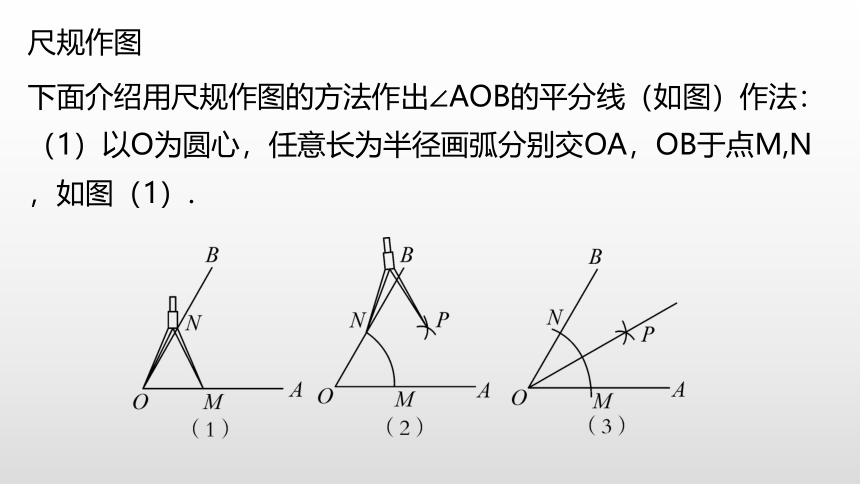
下面介绍用尺规作图的方法作出∠AOB的平分线(如图)作法:
(1)以O为圆心,任意长为半径画弧分别交OA,OB于点M,N,如图(1).
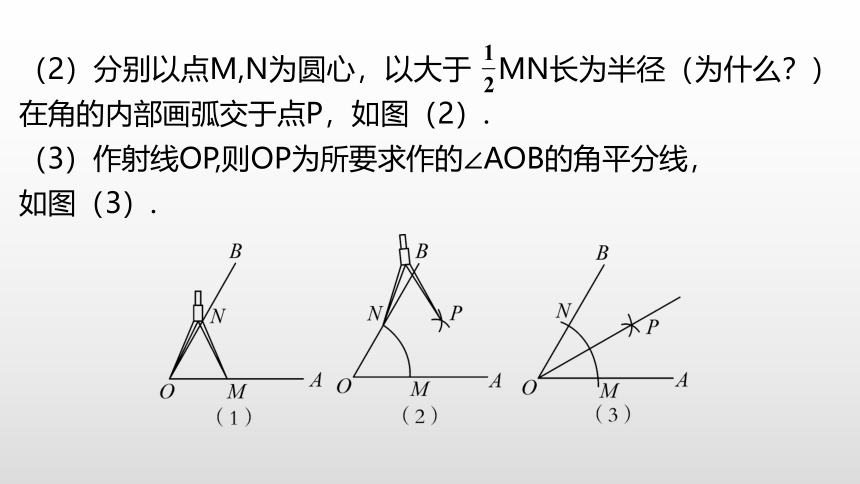
(2)分别以点M,N为圆心,以大于 MN长为半径(为什么?)在角的内部画弧交于点P,如图(2).
(3)作射线OP,则OP为所要求作的∠AOB的角平分线,
如图(3).
已知:直线AB和AB上一点C(如图).
求作:AB的垂线,使它经过点C.
作法:作平角∠ACB的平分线CF.
直线CF就是所求作的垂线.
1.经过已知直线上的一点作这条直线的垂线
已知:直线AB和AB外一点C
求作:AB的垂线,使它经过点C.
作法:(1)任意取一点K,使K和C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧交于点F;
(4)作直线CF.
直线CF就是所求作的垂线.
2.经过已知直线外一点作这条直线的垂线
[教材补充例题] 已知:∠MON,如图.
(1)求作:∠MON的平分线OC;(不写作图步骤,但保留作图痕迹)
例题精讲
解:(1)如图,射线OC即为∠MON的平分线.
(2)证明:如图,连接BC,AC.根据作法可得BC=AC,OA=OB.
在△OAC和△OBC中,
∵
∴△OAC≌△OBC.(SSS)
∴∠AOC=∠BOC,
即射线OC是∠MON的平分线.
(2)根据作法,请证明所作的射线OC就是∠MON的平分线.
[教材补充例题] 如图,已知△ABC,只用直尺和圆规作出△ABC的高AD.(尺规作图,保留作图痕迹,不写作法)
解:如图,线段AD就是所要作的高.
课堂小结
作角平分线的方法:(1)折纸法;(2)度量法;(3)尺规作图法.
[说明] 利用折纸法,我们发现角是轴对称图形,其对称轴是它的平分线所在的直线.
1.过直线上一点作已知直线的垂线就是作以已知点为顶点的平角的平分线.
2.过直线外一点作已知直线的垂线就是作已知直线上一条线段的垂直平分线.
随堂演练
1.用直尺和圆规作一个角的平分线的示意图如图,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角平分线上的点到角两边的距离相等
A
2.如图,请你在下列各图中,过点P画出射线AB或线段AB的垂线.
解:如图:
第十五章 轴对称图形与等腰三角形
15.4 角的平分线(第1课时)
知识导入
思考:如图AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画出一条射线AE,你能说一说“AE是否平分∠A,∠E呢?”
A
B
D
C(E)
新知讲解
怎样作出角的平分线?
通过折纸可以作出一个角的角平分线.在半透明纸上画一个角,请你用折叠的方法,找出角的平分线,如图.
B
A
C
A
D
C(B)
A
D
C
B
发现:角是轴对称图形,角平分线所在的直线是它的对称轴.
尺规作图
下面介绍用尺规作图的方法作出∠AOB的平分线(如图)作法:
(1)以O为圆心,任意长为半径画弧分别交OA,OB于点M,N,如图(1).
(2)分别以点M,N为圆心,以大于 MN长为半径(为什么?)在角的内部画弧交于点P,如图(2).
(3)作射线OP,则OP为所要求作的∠AOB的角平分线,
如图(3).
已知:直线AB和AB上一点C(如图).
求作:AB的垂线,使它经过点C.
作法:作平角∠ACB的平分线CF.
直线CF就是所求作的垂线.
1.经过已知直线上的一点作这条直线的垂线
已知:直线AB和AB外一点C
求作:AB的垂线,使它经过点C.
作法:(1)任意取一点K,使K和C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧交于点F;
(4)作直线CF.
直线CF就是所求作的垂线.
2.经过已知直线外一点作这条直线的垂线
[教材补充例题] 已知:∠MON,如图.
(1)求作:∠MON的平分线OC;(不写作图步骤,但保留作图痕迹)
例题精讲
解:(1)如图,射线OC即为∠MON的平分线.
(2)证明:如图,连接BC,AC.根据作法可得BC=AC,OA=OB.
在△OAC和△OBC中,
∵
∴△OAC≌△OBC.(SSS)
∴∠AOC=∠BOC,
即射线OC是∠MON的平分线.
(2)根据作法,请证明所作的射线OC就是∠MON的平分线.
[教材补充例题] 如图,已知△ABC,只用直尺和圆规作出△ABC的高AD.(尺规作图,保留作图痕迹,不写作法)
解:如图,线段AD就是所要作的高.
课堂小结
作角平分线的方法:(1)折纸法;(2)度量法;(3)尺规作图法.
[说明] 利用折纸法,我们发现角是轴对称图形,其对称轴是它的平分线所在的直线.
1.过直线上一点作已知直线的垂线就是作以已知点为顶点的平角的平分线.
2.过直线外一点作已知直线的垂线就是作已知直线上一条线段的垂直平分线.
随堂演练
1.用直尺和圆规作一个角的平分线的示意图如图,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角平分线上的点到角两边的距离相等
A
2.如图,请你在下列各图中,过点P画出射线AB或线段AB的垂线.
解:如图:
