沪科版数学八年级上册同步课时练习:15.3 第1课时 等腰三角形的性质 (word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步课时练习:15.3 第1课时 等腰三角形的性质 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 217.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
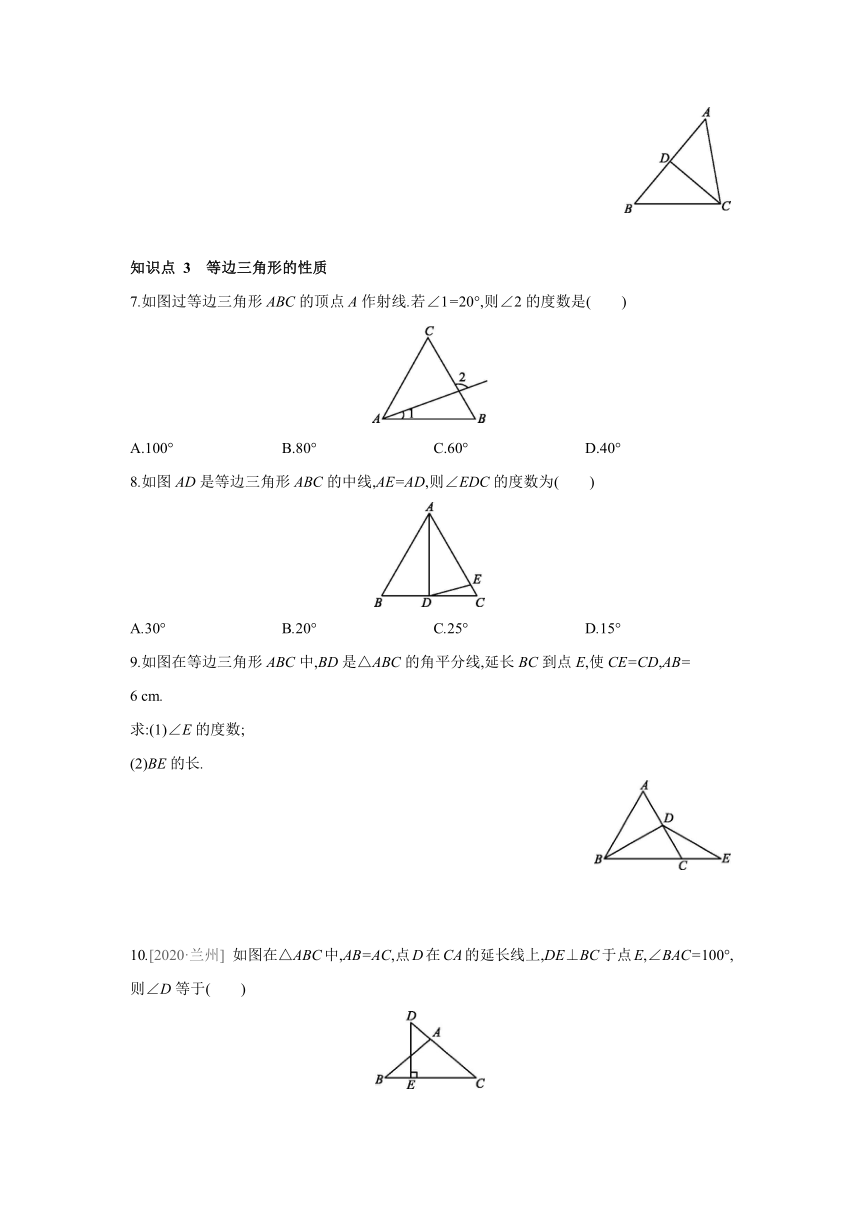
15.3 第1课时 等腰三角形的性质
知识点 1 等腰三角形的性质(等边对等角)
1.如图在等腰三角形ABC中,AB=AC,由于等腰三角形是轴对称形,若其底角∠B=35°,则∠C= °.
2.[2020·滨州] 在等腰三角形ABC中,AB=AC,若∠B=50°,则∠A的度数为 .
3.如图示,已知AB=AC,AD是△ABC的外角∠EAC的平分线.求证:AD∥BC.
知识点 2 等腰三角形的性质(“三线合一”)
4.如图在△ABC中,AB=AC,AD平分∠BAC,那么下列结论不一定成立的是( )
A.△ABD≌△ACD B.AD⊥BC
C.BD=CD D.AD=BD
5.[2020·福建] 如图AD是等腰三角形ABC的顶角的平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
6.[2020·合肥蜀山区期末] 如图在△ABC中,CA=CB,D是AB的中点,∠B=50°,求∠ACD的度数.
知识点 3 等边三角形的性质
7.如图过等边三角形ABC的顶点A作射线.若∠1=20°,则∠2的度数是( )
A.100° B.80° C.60° D.40°
8.如图AD是等边三角形ABC的中线,AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
9.如图在等边三角形ABC中,BD是△ABC的角平分线,延长BC到点E,使CE=CD,AB=
6 cm.
求:(1)∠E的度数;
(2)BE的长.
10.[2020·兰州] 如图在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D等于( )
A.40° B.50° C.60° D.80°
11.如图,AB∥CD,BE垂直平分AD,DC=BC,连接BD.若∠A=70°,则∠C的度数为( )
A.100° B.110° C.115° D.120°
12.如图,点B,C,E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
13.[2020·合肥蜀山区期末] 在△ABC中,D,E是边BC上的两点,DC=DA,EA=EB,∠DAE=40°,则∠BAC的度数是 .
14.[教材例1变式题] 已知:如图,在△ABC中,D,E是边BC上的两点,且BD=AD,CE=AE.
(1)若∠BAC=100°,求∠DAE的度数;
(2)若△ADE是等边三角形,求∠BAC的度数.
15.(1)如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=88°,求∠A的度数.
(2)如图②,∠MAN=11°,点B在AM上,且AB=1.按下列要求画:以点B为圆心,1为半径向右画弧交AN于点B1,得第1条线段BB1;再以点B1为圆心,1为半径向右画弧交AM于点B2,得第2条线段B1B2……这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段,则n为多少
答案
1.35
2.80° 解: ∵AB=AC,∠B=50°,∴∠C=∠B=50°,∴∠A=180°-2×50°=80°.
3.证明:∵AB=AC,∴∠B=∠C.
又∵∠EAC=∠B+∠C,
∴∠EAC=2∠B.
∵AD平分∠EAC,
∴∠EAC=2∠EAD.
∴∠EAD=∠B.∴AD∥BC.
4.D 解: 在△ABD和△ACD中,AB=AC,∠BAD=∠CAD,AD=AD,所以△ABD≌△ACD,所以A项正确;根据三角形全等可以得到AD⊥BC,BD=CD.故选D.
5.B
6.解:∵CA=CB,∴△ABC是等腰三角形.
∵∠B=50°,∴∠A=∠B=50°,
∴∠ACB=80°.
又∵D是AB的中点,
即CD是底边AB上的中线,
∴CD平分∠ACB,
∴∠ACD=∠ACB=40°.
7.A 解: 如图,∵△ABC是等边三角形,
∴∠B=60°.
又∵∠1=20°,
∴∠3=100°,
∴∠2=100°.故选A.
8.D 解: ∵AD是等边三角形ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,∴∠ADC=90°.
∵AD=AE,
∴∠ADE=∠AED=×(180°-∠CAD)=75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
9.解:(1)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E=∠ACB=30°.
(2)∵△ABC是等边三角形,BD是△ABC的角平分线,
∴AB=AC=BC,D是AC的中点.
又∵AB=6 cm,∴CD=3 cm,∴CE=3 cm,
∴BE=BC+CE=6+3=9(cm).
10.B 解: ∵AB=AC,∠BAC=100°,
∴∠C=∠B=40°.
∵DE⊥BC于点E,∴∠D=90°-∠C=90°-40°=50°.
11.A 解: ∵BE垂直平分AD,∴AB=DB.∴∠ABE=∠DBE.又∵∠A=70°,∴∠ABE=20°.
∴∠ABD=40°.又∵AB∥CD,∴∠CDB=∠ABD=40°.又∵DC=BC,∴∠C=180°-2×40°=100°.故选A.
12.D
13.110°或70° 解: 如图①,∵DC=DA,EA=EB,∴∠EAB=∠B,∠DAC=∠C.
∴∠AED=∠B+∠EAB=2∠B,∠ADE=∠C+∠DAC=2∠C.
又∵∠AED+∠ADE+∠DAE=180°,
∴2∠B+2∠C+∠DAE=180°,
∴2(∠B+∠C)=140°,
则∠B+∠C=70°,
∴∠BAC=110°.
如图②,∵DC=DA,EA=EB,
∴∠EAB=∠B,∠DAC=∠C.
∴∠AEC=∠B+∠EAB=2∠B,∠ADB=∠C+∠DAC=2∠C.
∵∠AEC+∠ADB=∠DAE+∠ADE+∠DAE+∠AED=180°+∠DAE=180°+40°=220°,
∴2∠B+2∠C=220°,
∴∠B+∠C=110°,∴∠BAC=70°.
14.解:(1)∵BD=AD,∴∠B=∠DAB.
∴∠ADE=2∠B.同理,∠AED=2∠C.
∵∠BAC=100°,∴∠B+∠C=80°.
∴∠DAE=180°-(∠ADE+∠AED)=180°-2(∠B+∠C)=20°.
(2)∵△ADE是等边三角形,
∴∠ADE=∠AED=60°.
∴∠B=30°,∠C=30°.
∴∠BAC=180°-(∠B+∠C)=180°-(30°+30°)=120°.
15.解:(1)∵AB=BC=CD=DE,
∴∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠CED.
根据三角形的外角性质,可得∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=
∠EDM.
设∠A=x°,则∠CBD=∠CDB=2x°,∠ECD=∠CED=3x°,∠EDM=4x°.
又∵∠EDM=88°,∴4x=88,
解得x=22.即∠A=22°.
(2)由题意可知,△ABB1,△BB1B2,△B1B2B3都是等腰三角形,第一个等腰三角形ABB1的底角为11°.
由三角形的外角性质可以得到,第二个等腰三角形BB1B2的底角为22°,第三个等腰三角形B1B2B3的底角为33°,
于是可得,第n个等腰三角形的底角为(11n)°,而等腰三角形的底角小于90°,
即11n<90,
∴n<=8,
∴n=8以后就不能再画出符合要求的线段了,
故n=8.
知识点 1 等腰三角形的性质(等边对等角)
1.如图在等腰三角形ABC中,AB=AC,由于等腰三角形是轴对称形,若其底角∠B=35°,则∠C= °.
2.[2020·滨州] 在等腰三角形ABC中,AB=AC,若∠B=50°,则∠A的度数为 .
3.如图示,已知AB=AC,AD是△ABC的外角∠EAC的平分线.求证:AD∥BC.
知识点 2 等腰三角形的性质(“三线合一”)
4.如图在△ABC中,AB=AC,AD平分∠BAC,那么下列结论不一定成立的是( )
A.△ABD≌△ACD B.AD⊥BC
C.BD=CD D.AD=BD
5.[2020·福建] 如图AD是等腰三角形ABC的顶角的平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
6.[2020·合肥蜀山区期末] 如图在△ABC中,CA=CB,D是AB的中点,∠B=50°,求∠ACD的度数.
知识点 3 等边三角形的性质
7.如图过等边三角形ABC的顶点A作射线.若∠1=20°,则∠2的度数是( )
A.100° B.80° C.60° D.40°
8.如图AD是等边三角形ABC的中线,AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
9.如图在等边三角形ABC中,BD是△ABC的角平分线,延长BC到点E,使CE=CD,AB=
6 cm.
求:(1)∠E的度数;
(2)BE的长.
10.[2020·兰州] 如图在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D等于( )
A.40° B.50° C.60° D.80°
11.如图,AB∥CD,BE垂直平分AD,DC=BC,连接BD.若∠A=70°,则∠C的度数为( )
A.100° B.110° C.115° D.120°
12.如图,点B,C,E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
13.[2020·合肥蜀山区期末] 在△ABC中,D,E是边BC上的两点,DC=DA,EA=EB,∠DAE=40°,则∠BAC的度数是 .
14.[教材例1变式题] 已知:如图,在△ABC中,D,E是边BC上的两点,且BD=AD,CE=AE.
(1)若∠BAC=100°,求∠DAE的度数;
(2)若△ADE是等边三角形,求∠BAC的度数.
15.(1)如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=88°,求∠A的度数.
(2)如图②,∠MAN=11°,点B在AM上,且AB=1.按下列要求画:以点B为圆心,1为半径向右画弧交AN于点B1,得第1条线段BB1;再以点B1为圆心,1为半径向右画弧交AM于点B2,得第2条线段B1B2……这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段,则n为多少
答案
1.35
2.80° 解: ∵AB=AC,∠B=50°,∴∠C=∠B=50°,∴∠A=180°-2×50°=80°.
3.证明:∵AB=AC,∴∠B=∠C.
又∵∠EAC=∠B+∠C,
∴∠EAC=2∠B.
∵AD平分∠EAC,
∴∠EAC=2∠EAD.
∴∠EAD=∠B.∴AD∥BC.
4.D 解: 在△ABD和△ACD中,AB=AC,∠BAD=∠CAD,AD=AD,所以△ABD≌△ACD,所以A项正确;根据三角形全等可以得到AD⊥BC,BD=CD.故选D.
5.B
6.解:∵CA=CB,∴△ABC是等腰三角形.
∵∠B=50°,∴∠A=∠B=50°,
∴∠ACB=80°.
又∵D是AB的中点,
即CD是底边AB上的中线,
∴CD平分∠ACB,
∴∠ACD=∠ACB=40°.
7.A 解: 如图,∵△ABC是等边三角形,
∴∠B=60°.
又∵∠1=20°,
∴∠3=100°,
∴∠2=100°.故选A.
8.D 解: ∵AD是等边三角形ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,∴∠ADC=90°.
∵AD=AE,
∴∠ADE=∠AED=×(180°-∠CAD)=75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
9.解:(1)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E=∠ACB=30°.
(2)∵△ABC是等边三角形,BD是△ABC的角平分线,
∴AB=AC=BC,D是AC的中点.
又∵AB=6 cm,∴CD=3 cm,∴CE=3 cm,
∴BE=BC+CE=6+3=9(cm).
10.B 解: ∵AB=AC,∠BAC=100°,
∴∠C=∠B=40°.
∵DE⊥BC于点E,∴∠D=90°-∠C=90°-40°=50°.
11.A 解: ∵BE垂直平分AD,∴AB=DB.∴∠ABE=∠DBE.又∵∠A=70°,∴∠ABE=20°.
∴∠ABD=40°.又∵AB∥CD,∴∠CDB=∠ABD=40°.又∵DC=BC,∴∠C=180°-2×40°=100°.故选A.
12.D
13.110°或70° 解: 如图①,∵DC=DA,EA=EB,∴∠EAB=∠B,∠DAC=∠C.
∴∠AED=∠B+∠EAB=2∠B,∠ADE=∠C+∠DAC=2∠C.
又∵∠AED+∠ADE+∠DAE=180°,
∴2∠B+2∠C+∠DAE=180°,
∴2(∠B+∠C)=140°,
则∠B+∠C=70°,
∴∠BAC=110°.
如图②,∵DC=DA,EA=EB,
∴∠EAB=∠B,∠DAC=∠C.
∴∠AEC=∠B+∠EAB=2∠B,∠ADB=∠C+∠DAC=2∠C.
∵∠AEC+∠ADB=∠DAE+∠ADE+∠DAE+∠AED=180°+∠DAE=180°+40°=220°,
∴2∠B+2∠C=220°,
∴∠B+∠C=110°,∴∠BAC=70°.
14.解:(1)∵BD=AD,∴∠B=∠DAB.
∴∠ADE=2∠B.同理,∠AED=2∠C.
∵∠BAC=100°,∴∠B+∠C=80°.
∴∠DAE=180°-(∠ADE+∠AED)=180°-2(∠B+∠C)=20°.
(2)∵△ADE是等边三角形,
∴∠ADE=∠AED=60°.
∴∠B=30°,∠C=30°.
∴∠BAC=180°-(∠B+∠C)=180°-(30°+30°)=120°.
15.解:(1)∵AB=BC=CD=DE,
∴∠A=∠BCA,∠CBD=∠CDB,∠DCE=∠CED.
根据三角形的外角性质,可得∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=
∠EDM.
设∠A=x°,则∠CBD=∠CDB=2x°,∠ECD=∠CED=3x°,∠EDM=4x°.
又∵∠EDM=88°,∴4x=88,
解得x=22.即∠A=22°.
(2)由题意可知,△ABB1,△BB1B2,△B1B2B3都是等腰三角形,第一个等腰三角形ABB1的底角为11°.
由三角形的外角性质可以得到,第二个等腰三角形BB1B2的底角为22°,第三个等腰三角形B1B2B3的底角为33°,
于是可得,第n个等腰三角形的底角为(11n)°,而等腰三角形的底角小于90°,
即11n<90,
∴n<=8,
∴n=8以后就不能再画出符合要求的线段了,
故n=8.
