沪科版数学八年级上册同步课时练习:15.3 第2课时 等腰三角形性质的应用 (word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步课时练习:15.3 第2课时 等腰三角形性质的应用 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 14:48:46 | ||
图片预览

文档简介
第2课时 等腰三角形性质的应用
知识点 等腰三角形性质的应用
1.[2020·临沂] 如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD等于 ( )
A.40° B.50° C.60° D.70°
2.[2019·衢州] “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”(②为①的示意)能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 ( )
A.60° B.65° C.75° D.80°
3.[2020·安庆期末] 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E.若∠CBD∶∠DBA=2∶1,则∠A的度数为( )
A.20° B.25° C.22.5° D.30°
4.[2019·重庆] 如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
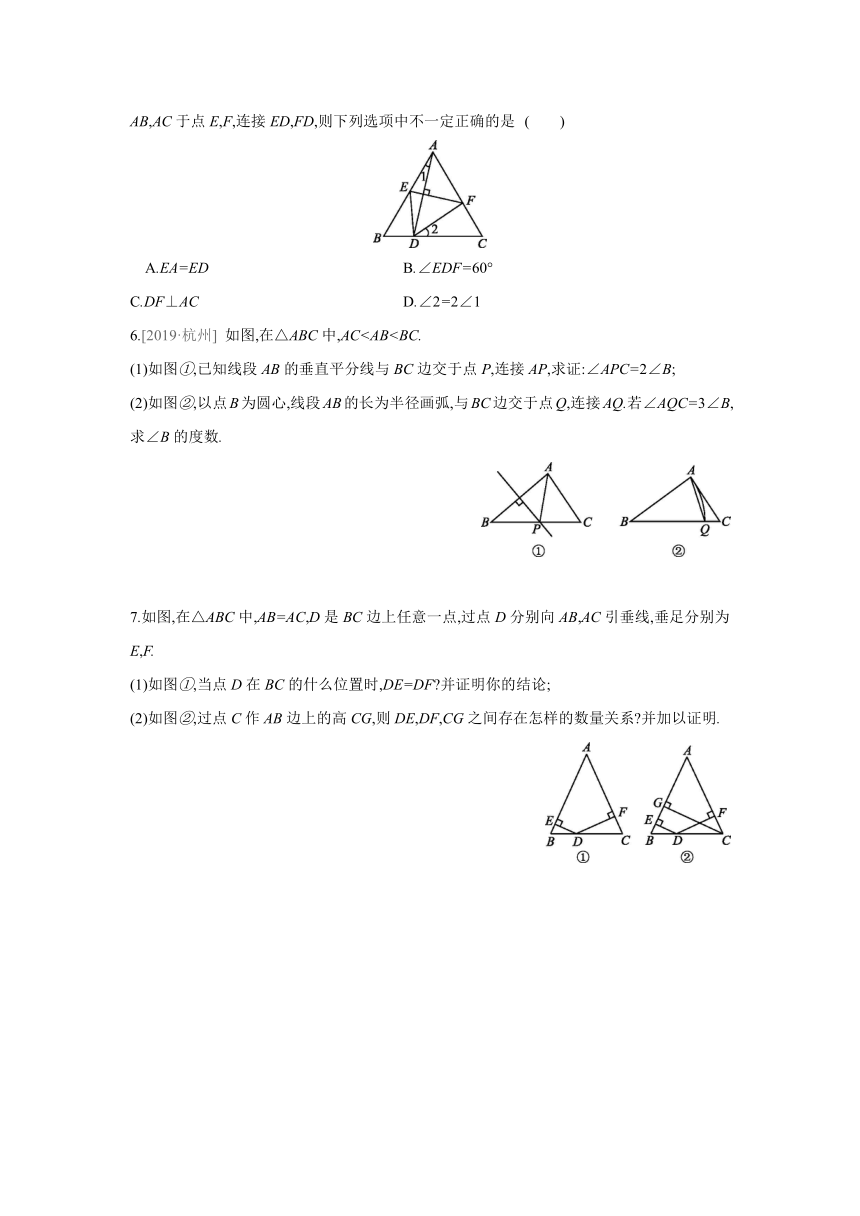
5.如图,等边三角形ABC中,D是边BC上不与两端点重合的点,线段AD的垂直平分线分别交AB,AC于点E,F,连接ED,FD,则下列选项中不一定正确的是 ( )
A.EA=ED B.∠EDF=60°
C.DF⊥AC D.∠2=2∠1
6.[2019·杭州] 如图,在△ABC中,AC(1)如图①,已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B;
(2)如图②,以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
7.如图,在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图①,当点D在BC的什么位置时,DE=DF 并证明你的结论;
(2)如图②,过点C作AB边上的高CG,则DE,DF,CG之间存在怎样的数量关系 并加以证明.
答案
1.D 解: ∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=70°.
∵CD∥AB,
∴∠BCD=∠ABC=70°.
2.D 解: ∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DEC=∠DCE=∠O+∠ODC=2∠ODC.
∴∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°.
∵∠CDE+∠ODC=180°-∠BDE=180°-75°=105°,
∴∠CDE=105°-∠ODC=105°-25°=80°.
故选D.
3.C 解: ∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠DBA.
∵∠CBD∶∠DBA=2∶1,
∴在△ABC中,∠A+∠ABC=∠A+∠A+2∠A=90°,
解得∠A=22.5°.
4.解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠C=42°,
∴∠BAD=∠CAD=90°-42°=48°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AC,∴∠F=∠CAD,
∴∠BAD=∠F,∴AE=FE.
5.C 解: ∵EF是AD的垂直平分线,
∴EA=ED,FA=FD,选项A正确;
∵△ABC是等边三角形,
∴∠BAC=∠B=60°.
∵EA=ED,FA=FD,
∴∠EDA=∠1,∠FAD=∠FDA,
∴∠EDF=∠EDA+∠FDA=∠BAC=60°,
选项B正确;
∵∠BED=∠1+∠EDA=2∠1,∠EDC=∠EDF+∠2=∠B+∠BED,
∴60°+∠2=60°+2∠1,
∴∠2=2∠1,
选项D正确;
不一定正确的是选项C.
故选C.
6.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,
∴PA=PB,
∴∠B=∠BAP.
∵∠APC=∠B+∠BAP,
∴∠APC=2∠B.
(2)根据题意可知BA=BQ,
∴∠BAQ=∠BQA.
∵∠AQC=3∠B,且∠AQC=∠B+∠BAQ,
∴∠BAQ=2∠B.
∵∠BAQ+∠BQA+∠B=180°,
∴5∠B=180°,
∴∠B=36°.
7.解:(1)当D是BC的中点时,DE=DF.
证明:∵AB=AC,∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC.
∵D是BC的中点,∴BD=CD.
在△DEB和△DFC中,
∵
∴△DEB≌△DFC.
∴DE=DF.
(2)DE+DF=CG.
证明:如图,连接AD.
由题意,知
S△ABD=AB·DE,S△ACD=AC·DF,S△ABC=AB·CG.
∵S△ABD+S△ACD=S△ABC,
∴AB·DE+AC·DF=AB·CG.
又∵AB=AC,
∴DE+DF=CG.
知识点 等腰三角形性质的应用
1.[2020·临沂] 如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD等于 ( )
A.40° B.50° C.60° D.70°
2.[2019·衢州] “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”(②为①的示意)能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 ( )
A.60° B.65° C.75° D.80°
3.[2020·安庆期末] 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E.若∠CBD∶∠DBA=2∶1,则∠A的度数为( )
A.20° B.25° C.22.5° D.30°
4.[2019·重庆] 如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
5.如图,等边三角形ABC中,D是边BC上不与两端点重合的点,线段AD的垂直平分线分别交AB,AC于点E,F,连接ED,FD,则下列选项中不一定正确的是 ( )
A.EA=ED B.∠EDF=60°
C.DF⊥AC D.∠2=2∠1
6.[2019·杭州] 如图,在△ABC中,AC
(2)如图②,以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
7.如图,在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图①,当点D在BC的什么位置时,DE=DF 并证明你的结论;
(2)如图②,过点C作AB边上的高CG,则DE,DF,CG之间存在怎样的数量关系 并加以证明.
答案
1.D 解: ∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=70°.
∵CD∥AB,
∴∠BCD=∠ABC=70°.
2.D 解: ∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DEC=∠DCE=∠O+∠ODC=2∠ODC.
∴∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°.
∵∠CDE+∠ODC=180°-∠BDE=180°-75°=105°,
∴∠CDE=105°-∠ODC=105°-25°=80°.
故选D.
3.C 解: ∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠DBA.
∵∠CBD∶∠DBA=2∶1,
∴在△ABC中,∠A+∠ABC=∠A+∠A+2∠A=90°,
解得∠A=22.5°.
4.解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠C=42°,
∴∠BAD=∠CAD=90°-42°=48°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AC,∴∠F=∠CAD,
∴∠BAD=∠F,∴AE=FE.
5.C 解: ∵EF是AD的垂直平分线,
∴EA=ED,FA=FD,选项A正确;
∵△ABC是等边三角形,
∴∠BAC=∠B=60°.
∵EA=ED,FA=FD,
∴∠EDA=∠1,∠FAD=∠FDA,
∴∠EDF=∠EDA+∠FDA=∠BAC=60°,
选项B正确;
∵∠BED=∠1+∠EDA=2∠1,∠EDC=∠EDF+∠2=∠B+∠BED,
∴60°+∠2=60°+2∠1,
∴∠2=2∠1,
选项D正确;
不一定正确的是选项C.
故选C.
6.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,
∴PA=PB,
∴∠B=∠BAP.
∵∠APC=∠B+∠BAP,
∴∠APC=2∠B.
(2)根据题意可知BA=BQ,
∴∠BAQ=∠BQA.
∵∠AQC=3∠B,且∠AQC=∠B+∠BAQ,
∴∠BAQ=2∠B.
∵∠BAQ+∠BQA+∠B=180°,
∴5∠B=180°,
∴∠B=36°.
7.解:(1)当D是BC的中点时,DE=DF.
证明:∵AB=AC,∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC.
∵D是BC的中点,∴BD=CD.
在△DEB和△DFC中,
∵
∴△DEB≌△DFC.
∴DE=DF.
(2)DE+DF=CG.
证明:如图,连接AD.
由题意,知
S△ABD=AB·DE,S△ACD=AC·DF,S△ABC=AB·CG.
∵S△ABD+S△ACD=S△ABC,
∴AB·DE+AC·DF=AB·CG.
又∵AB=AC,
∴DE+DF=CG.
