沪科版数学八年级上册15.3 第3课时 等腰三角形的判定 同步课时练习(word版 含解析)
文档属性
| 名称 | 沪科版数学八年级上册15.3 第3课时 等腰三角形的判定 同步课时练习(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 201.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

文档简介
第3课时 等腰三角形的判定
知识点 1 等腰三角形的判定
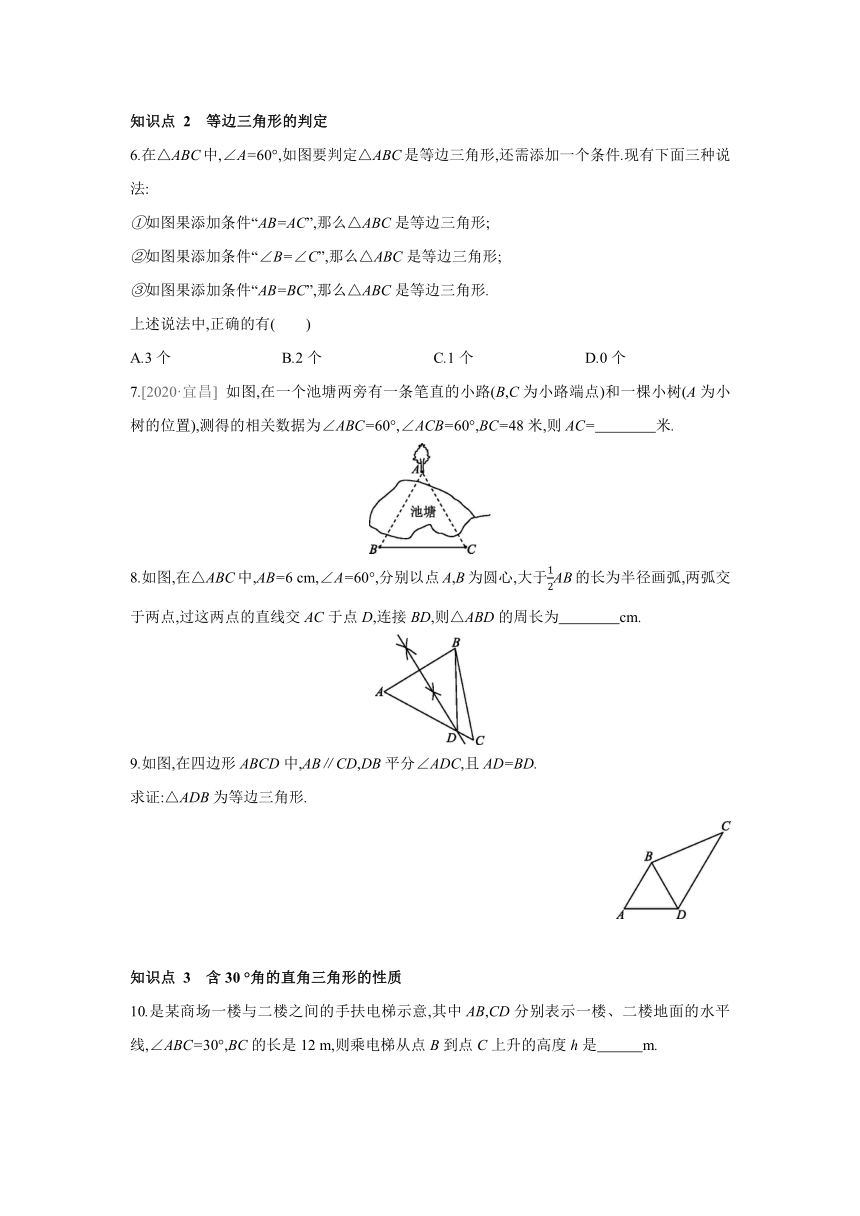
1.如图,在△ABC中,已知∠B=∠C,则( )
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.下列选项中,能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
3.如图,上午8时,一艘船从海岛A出发,以15 n mile/h的速度向正北方向航行,10时到达海岛B处,分别从A,B处观测灯塔C,测得∠NAC=42°,∠NBC=84°,则从海岛B到灯塔C的距离为( )
A.45 n mile B.30 n mile C.20 n mile D.15 n mile
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则中的等腰三角形有( )
A.3个 B.4个 C.5个 D.6个
5.如图,在△ABC中,D是BA延长线上的一点,AE∥BC,AE平分∠DAC.求证:△ABC是等腰三角形.
知识点 2 等边三角形的判定
6.在△ABC中,∠A=60°,如图要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如图果添加条件“AB=AC”,那么△ABC是等边三角形;
②如图果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如图果添加条件“AB=BC”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A.3个 B.2个 C.1个 D.0个
7.[2020·宜昌] 如图,在一个池塘两旁有一条笔直的小路(B,C为小路端点)和一棵小树(A为小树的位置),测得的相关数据为∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
8.如图,在△ABC中,AB=6 cm,∠A=60°,分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于两点,过这两点的直线交AC于点D,连接BD,则△ABD的周长为 cm.
9.如图,在四边形ABCD中,AB∥CD,DB平分∠ADC,且AD=BD.
求证:△ADB为等边三角形.
知识点 3 含30 °角的直角三角形的性质
10.是某商场一楼与二楼之间的手扶电梯示意,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=30°,BC的长是12 m,则乘电梯从点B到点C上升的高度h是 m.
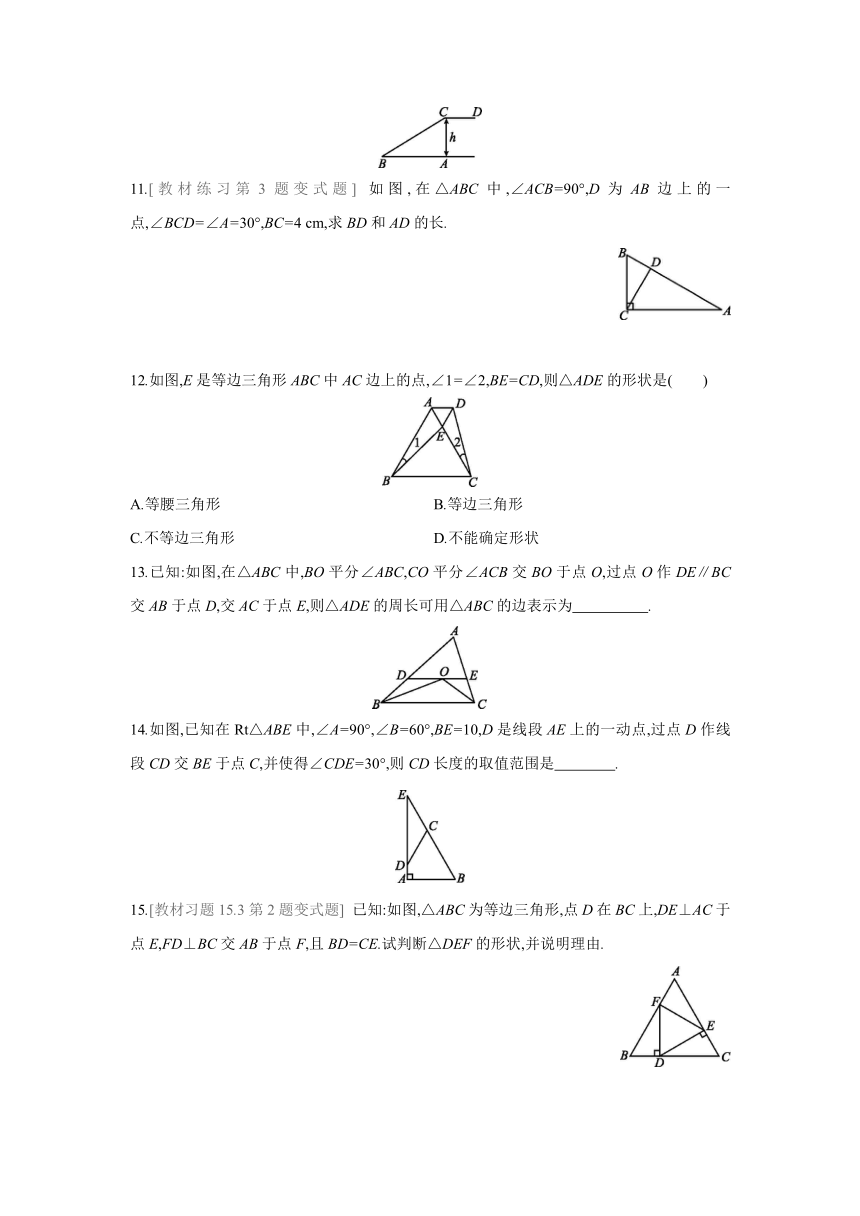
11.[教材练习第3题变式题] 如图,在△ABC中,∠ACB=90°,D为AB边上的一点,∠BCD=∠A=30°,BC=4 cm,求BD和AD的长.
12.如图,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
13.已知:如图,在△ABC中,BO平分∠ABC,CO平分∠ACB交BO于点O,过点O作DE∥BC交AB于点D,交AC于点E,则△ADE的周长可用△ABC的边表示为 .
14.如图,已知在Rt△ABE中,∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过点D作线段CD交BE于点C,并使得∠CDE=30°,则CD长度的取值范围是 .
15.[教材习题15.3第2题变式题] 已知:如图,△ABC为等边三角形,点D在BC上,DE⊥AC于点E,FD⊥BC交AB于点F,且BD=CE.试判断△DEF的形状,并说明理由.
16.[2020·阜阳颍州区期末] 如图,点E在△ABC的AC边的延长线上,点D在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.
答案
1.B 解: 根据等角对等边即可得到相等的边.
2.C 解: 选项A中,求出∠C=90°,三角形中没有两个相等的角,不是等腰三角形;
B选项中,求出∠C=80°,三角形中没有两个相等的角,不是等腰三角形;
C选项中,求出∠C=80°,所以∠B=∠C,根据“等角对等边”,△ABC是等腰三角形;
D选项中,求出∠C=60°,三角形中没有两个相等的角,不是等腰三角形.
3.B 4.D
5.证明:∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C.
∵AE平分∠DAC,
∴∠DAE=∠EAC.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
6.A 解: ①若添加的条件为AB=AC,由∠A=60°,则利用有一个角为60°的等腰三角形为等边三角形,可得出△ABC为等边三角形;
②若添加条件为∠B=∠C,
又∵∠A=60°,∴∠B=∠C=60°,
∴∠A=∠B=∠C,则△ABC为等边三角形;
③若添加的条件为AB=BC,由∠A=60°,则利用有一个角为60°的等腰三角形为等边三角形,可得出△ABC为等边三角形.
7.48 解: ∵∠ABC=60°,∠ACB=60°,∴∠BAC=60°,∴△ABC是等边三角形.∵BC=48米,∴AC=48米.
8.18 解: 由作可知,AD=BD,则可判定△ABD是等边三角形.
9.证明:∵DB平分∠ADC,
∴∠ADB=∠CDB.
∵AB∥CD,∴∠ABD=∠CDB,
∴∠ABD=∠ADB,
∴AB=AD.又∵AD=BD,∴AB=AD=BD.
∴△ADB为等边三角形.
10.6 解: 根据直角三角形中30°角所对的直角边等于斜边的一半,即可求解.
11.解:∵在△ABC中,∠ACB=90°,∠A=30°,BC=4 cm,
∴AB=2BC=8 cm,∠B=60°.
∵∠BCD=∠A=30°,
∴∠B+∠BCD=60°+30°=90°,
∴∠CDB=90°,
∴BD=BC=2 cm,
∴AD=AB-BD=8-2=6(cm).
12.B 解: ∵△ABC为等边三角形,∴∠BAC=60°,AB=AC.又∵∠1=∠2,BE=CD,
∴△ABE≌△ACD.∴AE=AD,∠BAE=∠CAD=60°.∴△ADE是等边三角形.故选B.
13.AB+AC 解: ∵BO平分∠ABC,CO平分∠ACB,
∴∠DBO=∠OBC,∠ECO=∠BCO.
∵DE∥BC,
∴∠DOB=∠OBC,∠COE=∠BCO,
∴∠DOB=∠DBO,∠COE=∠ECO,
∴BD=DO,OE=CE,
∴△ADE的周长=AD+DO+OE+AE=AD+BD+CE+AE=AB+AC.
14.0∵∠BAE=90°,∠B=60°,∴∠E=30°.
∴∠CDE=∠E,∠CDB=∠B.
∴CE=CD,CD=CB.
∴CD=BE=5.∴015.解:△DEF为等边三角形.理由如图下:
∵△ABC是等边三角形,∴∠B=∠C=60°.
∵DE⊥AC,FD⊥BC,
∴∠BDF=∠CED=90°.
在△BDF和△CED中,∵
∴△BDF≌△CED.∴DF=DE.
∵∠CDE=90°-60°=30°,
∴∠EDF=180°-90°-30°=60°.
又∵DF=DE,∴△DEF为等边三角形.
16.证明:过点D作DG∥AC交BC于点G,如图所示.
∵DG∥AC,
∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
∵
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,∴BD=GD,
∴∠B=∠DGB,∴∠B=∠ACB,
则AB=AC,
∴△ABC是等腰三角形.
知识点 1 等腰三角形的判定
1.如图,在△ABC中,已知∠B=∠C,则( )
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.下列选项中,能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
3.如图,上午8时,一艘船从海岛A出发,以15 n mile/h的速度向正北方向航行,10时到达海岛B处,分别从A,B处观测灯塔C,测得∠NAC=42°,∠NBC=84°,则从海岛B到灯塔C的距离为( )
A.45 n mile B.30 n mile C.20 n mile D.15 n mile
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则中的等腰三角形有( )
A.3个 B.4个 C.5个 D.6个
5.如图,在△ABC中,D是BA延长线上的一点,AE∥BC,AE平分∠DAC.求证:△ABC是等腰三角形.
知识点 2 等边三角形的判定
6.在△ABC中,∠A=60°,如图要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如图果添加条件“AB=AC”,那么△ABC是等边三角形;
②如图果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如图果添加条件“AB=BC”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A.3个 B.2个 C.1个 D.0个
7.[2020·宜昌] 如图,在一个池塘两旁有一条笔直的小路(B,C为小路端点)和一棵小树(A为小树的位置),测得的相关数据为∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
8.如图,在△ABC中,AB=6 cm,∠A=60°,分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于两点,过这两点的直线交AC于点D,连接BD,则△ABD的周长为 cm.
9.如图,在四边形ABCD中,AB∥CD,DB平分∠ADC,且AD=BD.
求证:△ADB为等边三角形.
知识点 3 含30 °角的直角三角形的性质
10.是某商场一楼与二楼之间的手扶电梯示意,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=30°,BC的长是12 m,则乘电梯从点B到点C上升的高度h是 m.
11.[教材练习第3题变式题] 如图,在△ABC中,∠ACB=90°,D为AB边上的一点,∠BCD=∠A=30°,BC=4 cm,求BD和AD的长.
12.如图,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
13.已知:如图,在△ABC中,BO平分∠ABC,CO平分∠ACB交BO于点O,过点O作DE∥BC交AB于点D,交AC于点E,则△ADE的周长可用△ABC的边表示为 .
14.如图,已知在Rt△ABE中,∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过点D作线段CD交BE于点C,并使得∠CDE=30°,则CD长度的取值范围是 .
15.[教材习题15.3第2题变式题] 已知:如图,△ABC为等边三角形,点D在BC上,DE⊥AC于点E,FD⊥BC交AB于点F,且BD=CE.试判断△DEF的形状,并说明理由.
16.[2020·阜阳颍州区期末] 如图,点E在△ABC的AC边的延长线上,点D在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.
答案
1.B 解: 根据等角对等边即可得到相等的边.
2.C 解: 选项A中,求出∠C=90°,三角形中没有两个相等的角,不是等腰三角形;
B选项中,求出∠C=80°,三角形中没有两个相等的角,不是等腰三角形;
C选项中,求出∠C=80°,所以∠B=∠C,根据“等角对等边”,△ABC是等腰三角形;
D选项中,求出∠C=60°,三角形中没有两个相等的角,不是等腰三角形.
3.B 4.D
5.证明:∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C.
∵AE平分∠DAC,
∴∠DAE=∠EAC.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
6.A 解: ①若添加的条件为AB=AC,由∠A=60°,则利用有一个角为60°的等腰三角形为等边三角形,可得出△ABC为等边三角形;
②若添加条件为∠B=∠C,
又∵∠A=60°,∴∠B=∠C=60°,
∴∠A=∠B=∠C,则△ABC为等边三角形;
③若添加的条件为AB=BC,由∠A=60°,则利用有一个角为60°的等腰三角形为等边三角形,可得出△ABC为等边三角形.
7.48 解: ∵∠ABC=60°,∠ACB=60°,∴∠BAC=60°,∴△ABC是等边三角形.∵BC=48米,∴AC=48米.
8.18 解: 由作可知,AD=BD,则可判定△ABD是等边三角形.
9.证明:∵DB平分∠ADC,
∴∠ADB=∠CDB.
∵AB∥CD,∴∠ABD=∠CDB,
∴∠ABD=∠ADB,
∴AB=AD.又∵AD=BD,∴AB=AD=BD.
∴△ADB为等边三角形.
10.6 解: 根据直角三角形中30°角所对的直角边等于斜边的一半,即可求解.
11.解:∵在△ABC中,∠ACB=90°,∠A=30°,BC=4 cm,
∴AB=2BC=8 cm,∠B=60°.
∵∠BCD=∠A=30°,
∴∠B+∠BCD=60°+30°=90°,
∴∠CDB=90°,
∴BD=BC=2 cm,
∴AD=AB-BD=8-2=6(cm).
12.B 解: ∵△ABC为等边三角形,∴∠BAC=60°,AB=AC.又∵∠1=∠2,BE=CD,
∴△ABE≌△ACD.∴AE=AD,∠BAE=∠CAD=60°.∴△ADE是等边三角形.故选B.
13.AB+AC 解: ∵BO平分∠ABC,CO平分∠ACB,
∴∠DBO=∠OBC,∠ECO=∠BCO.
∵DE∥BC,
∴∠DOB=∠OBC,∠COE=∠BCO,
∴∠DOB=∠DBO,∠COE=∠ECO,
∴BD=DO,OE=CE,
∴△ADE的周长=AD+DO+OE+AE=AD+BD+CE+AE=AB+AC.
14.0
∴∠CDE=∠E,∠CDB=∠B.
∴CE=CD,CD=CB.
∴CD=BE=5.∴0
∵△ABC是等边三角形,∴∠B=∠C=60°.
∵DE⊥AC,FD⊥BC,
∴∠BDF=∠CED=90°.
在△BDF和△CED中,∵
∴△BDF≌△CED.∴DF=DE.
∵∠CDE=90°-60°=30°,
∴∠EDF=180°-90°-30°=60°.
又∵DF=DE,∴△DEF为等边三角形.
16.证明:过点D作DG∥AC交BC于点G,如图所示.
∵DG∥AC,
∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
∵
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,∴BD=GD,
∴∠B=∠DGB,∴∠B=∠ACB,
则AB=AC,
∴△ABC是等腰三角形.
