沪科版数学八年级上册 15.4 第2课时 角的平分线的性质与判定 同步课时练习(word版 含解析)
文档属性
| 名称 | 沪科版数学八年级上册 15.4 第2课时 角的平分线的性质与判定 同步课时练习(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
第2课时 角的平分线的性质与判定
知识点 1 角的平分线的性质
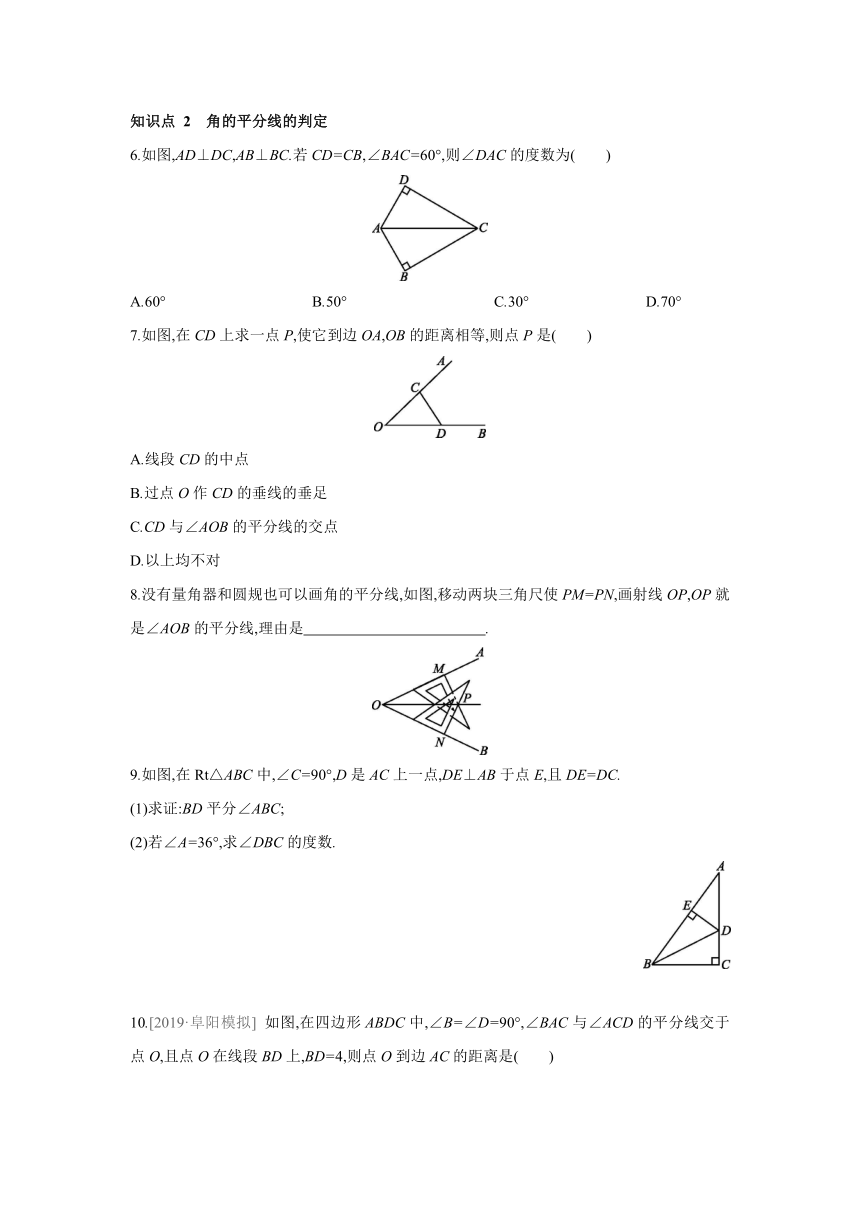
1.[2020·怀化] 如图在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E,若BD=3,则DE的长为( )
A.3 B. C.2 D.6
2.[2020·合肥瑶海区期末] 如图在Rt△ABC中,∠C=90°,用尺规作法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3
C.4 D.无法确定
3.[2020·潜山期末] 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E,∠AFD=90°,DE=2,则DF= .
4.[2020·宣城期末] 如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30 cm,BD∶CD=
3∶2,则点D到AB的距离为 cm.
5.[教材习题15.4第2题变式题] 已知:如图,BD平分∠ABC,∠A=∠C,点P在BD上,PM⊥AD,PN⊥CD,M,N为垂足.
求证:PM=PN.
知识点 2 角的平分线的判定
6.如图,AD⊥DC,AB⊥BC.若CD=CB,∠BAC=60°,则∠DAC的度数为( )
A.60° B.50° C.30° D.70°
7.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.过点O作CD的垂线的垂足
C.CD与∠AOB的平分线的交点
D.以上均不对
8.没有量角器和圆规也可以画角的平分线,如图,移动两块三角尺使PM=PN,画射线OP,OP就是∠AOB的平分线,理由是 .
9.如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,且DE=DC.
(1)求证:BD平分∠ABC;
(2)若∠A=36°,求∠DBC的度数.
10.[2019·阜阳模拟] 如图,在四边形ABDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )
A.1 B.1.5 C.2 D.3
11.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=5,BC=7,S△ABC=12,则DE的长为 .
12.如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,连接RS.若AQ=PQ,PR=PS,有下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 .
13.[教材练习第2题变式题] 已知:如图,CD为Rt△ABC斜边AB上的高,AB=8,∠BAC的平分线与CD,CB分别交于点E,F,FG⊥AB,垂足为G.若△ABF的面积为8,求CE的长.
14.如图,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
15.已知△DCE的顶点C在∠AOB的平分线OP上,CD交OA于点F,CE交OB于点G.
(1)如图①,若CD⊥OA,CE⊥OB,则中有哪些相等的线段,请直接写出你的结论: ;
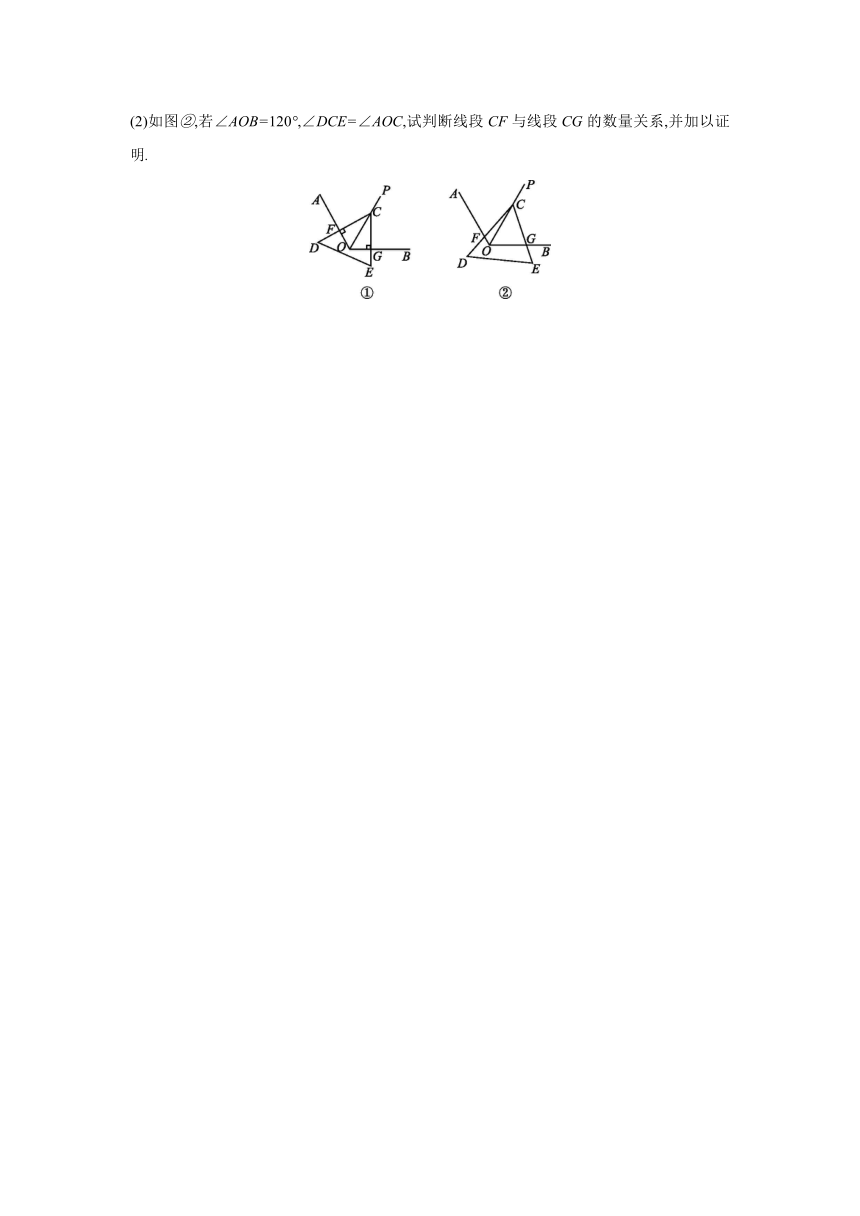
(2)如图②,若∠AOB=120°,∠DCE=∠AOC,试判断线段CF与线段CG的数量关系,并加以证明.
答案
1.A 解: ∵∠B=90°,∴DB⊥AB.又∵AD平分∠BAC,DE⊥AC,∴DE=BD=3.
2.A 解: 当DP⊥AB时,根据垂线段最短可知,此时PD的值最小.
由作可知AE平分∠BAC.
∵DC⊥AC,PD⊥AB,
∴DP=CD=2,
∴PD的最小值为2.
3.2 解: ∵AD是∠BAC的平分线,DE⊥AB,∠AFD=90°,∴DF=DE=2.
4.12 解: ∵BC=30 cm,BD∶CD=3∶2,∴CD=12 cm.∵∠C=90°,AD平分∠BAC,∴点D到边AB的距离=CD=12 cm.
5.证明:∵BD平分∠ABC,∴∠ABD=∠CBD.
又∵∠A=∠C,
∴∠ADB=∠CDB.
即DB平分∠ADC.
∵点P在DB上,PM⊥AD,PN⊥CD,
∴PM=PN.
6.A
7.C 解: ∵点P到边OA,OB的距离相等,
∴点P在∠AOB的平分线上,
∴点P为CD与∠AOB的平分线的交点.
8.角的内部到角两边距离相等的点在角的平分线上
9.解:(1)证明:∵∠C=90°,DE⊥AB,DE=DC,
∴点D在∠ABC的平分线上.
∴BD平分∠ABC.
(2)∵∠C=90°,∠A=36°,
∴∠ABC=54°.
∵BD平分∠ABC,
∴∠DBC=∠ABC=27°.
10.C 解: 如图,过点O作OE⊥AC于点E.
∵∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,
∴OB=OE=OD.
∵BD=4,
∴OB=OE=OD=2,
∴点O到边AC的距离是2.故选C.
11.2 解: 过点D作DF⊥AB于点F.
∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DE=DF.
∵AB·DF+BC·DE=S△ABC,
∴×5×DE+×7×DE=12,
解得DE=2.
12.①②④ 解: ①∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠BAC的平分线上,∠ARP=∠ASP=90°.
∴∠SAP=∠RAP.
又∵AP=AP,
∴△APR≌△APS.(AAS)
∴AR=AS.故①正确.
②∵AQ=PQ,∴∠QAP=∠QPA.
∵∠QAP=∠BAP,
∴∠QPA=∠BAP.
∴QP∥AR.故②正确.
③在Rt△BRP和Rt△QSP中,只有PR=PS,
不满足判定三角形全等的条件,故③错误.
④∵△APR≌△APS,
∴AR=AS,PQ=PS,
∴AP垂直平分RS.故④正确.
13.解:∵CD为Rt△ABC斜边AB上的高,FG⊥AB,
∴CD∥FG.∴∠GFE=∠FEC.
∵AF是∠BAC的平分线,
∴∠CAF=∠BAF.
又∵∠ACB是直角,FG⊥AB,
∴∠GFE=∠CFE.
∴∠CFE=∠FEC.
∴CE=CF.
∵AF是∠BAC的平分线,∠ACB是直角,FG⊥AB,
∴FG=CF.∴CE=FG.
∵△ABF的面积为8,AB=8,
∴FG=2.
∴CE=2.
14.解:(1)证明:∵BD,CE是△ABC的高,
∴∠BDC=∠CEB=90°.
∵OB=OC,∴∠OBC=∠OCB.
又∵BC=CB,∴△BEC≌△CDB.
∴∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:∵△BEC≌△CDB,∴CE=BD.
又∵OB=OC,∴OD=OE.
又∵OD⊥AC,OE⊥AB,
∴点O在∠BAC的平分线上.
15.解:(1)CF=CG,OF=OG
(2)CF=CG.
证明:如图,过点C作CM⊥OA于点M,CN⊥OB于点N,
∴∠CMF=∠CNG=90°.
∵OC平分∠AOB,∠AOB=120°,
∴CM=CN,∠AOC=∠BOC=∠DCE=60°,
∠MCN=360°-∠AOB-∠CMF-∠CNO=60°.
∴∠DCE=∠MCN.
∴∠MCN-∠FCN=∠DCE-∠FCN,
即∠1=∠2.
在△CMF与△CNG中,∵
∴△CMF≌△CNG.∴CF=CG.
知识点 1 角的平分线的性质
1.[2020·怀化] 如图在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E,若BD=3,则DE的长为( )
A.3 B. C.2 D.6
2.[2020·合肥瑶海区期末] 如图在Rt△ABC中,∠C=90°,用尺规作法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3
C.4 D.无法确定
3.[2020·潜山期末] 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E,∠AFD=90°,DE=2,则DF= .
4.[2020·宣城期末] 如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30 cm,BD∶CD=
3∶2,则点D到AB的距离为 cm.
5.[教材习题15.4第2题变式题] 已知:如图,BD平分∠ABC,∠A=∠C,点P在BD上,PM⊥AD,PN⊥CD,M,N为垂足.
求证:PM=PN.
知识点 2 角的平分线的判定
6.如图,AD⊥DC,AB⊥BC.若CD=CB,∠BAC=60°,则∠DAC的度数为( )
A.60° B.50° C.30° D.70°
7.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.过点O作CD的垂线的垂足
C.CD与∠AOB的平分线的交点
D.以上均不对
8.没有量角器和圆规也可以画角的平分线,如图,移动两块三角尺使PM=PN,画射线OP,OP就是∠AOB的平分线,理由是 .
9.如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,且DE=DC.
(1)求证:BD平分∠ABC;
(2)若∠A=36°,求∠DBC的度数.
10.[2019·阜阳模拟] 如图,在四边形ABDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )
A.1 B.1.5 C.2 D.3
11.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=5,BC=7,S△ABC=12,则DE的长为 .
12.如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,连接RS.若AQ=PQ,PR=PS,有下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 .
13.[教材练习第2题变式题] 已知:如图,CD为Rt△ABC斜边AB上的高,AB=8,∠BAC的平分线与CD,CB分别交于点E,F,FG⊥AB,垂足为G.若△ABF的面积为8,求CE的长.
14.如图,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
15.已知△DCE的顶点C在∠AOB的平分线OP上,CD交OA于点F,CE交OB于点G.
(1)如图①,若CD⊥OA,CE⊥OB,则中有哪些相等的线段,请直接写出你的结论: ;
(2)如图②,若∠AOB=120°,∠DCE=∠AOC,试判断线段CF与线段CG的数量关系,并加以证明.
答案
1.A 解: ∵∠B=90°,∴DB⊥AB.又∵AD平分∠BAC,DE⊥AC,∴DE=BD=3.
2.A 解: 当DP⊥AB时,根据垂线段最短可知,此时PD的值最小.
由作可知AE平分∠BAC.
∵DC⊥AC,PD⊥AB,
∴DP=CD=2,
∴PD的最小值为2.
3.2 解: ∵AD是∠BAC的平分线,DE⊥AB,∠AFD=90°,∴DF=DE=2.
4.12 解: ∵BC=30 cm,BD∶CD=3∶2,∴CD=12 cm.∵∠C=90°,AD平分∠BAC,∴点D到边AB的距离=CD=12 cm.
5.证明:∵BD平分∠ABC,∴∠ABD=∠CBD.
又∵∠A=∠C,
∴∠ADB=∠CDB.
即DB平分∠ADC.
∵点P在DB上,PM⊥AD,PN⊥CD,
∴PM=PN.
6.A
7.C 解: ∵点P到边OA,OB的距离相等,
∴点P在∠AOB的平分线上,
∴点P为CD与∠AOB的平分线的交点.
8.角的内部到角两边距离相等的点在角的平分线上
9.解:(1)证明:∵∠C=90°,DE⊥AB,DE=DC,
∴点D在∠ABC的平分线上.
∴BD平分∠ABC.
(2)∵∠C=90°,∠A=36°,
∴∠ABC=54°.
∵BD平分∠ABC,
∴∠DBC=∠ABC=27°.
10.C 解: 如图,过点O作OE⊥AC于点E.
∵∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,
∴OB=OE=OD.
∵BD=4,
∴OB=OE=OD=2,
∴点O到边AC的距离是2.故选C.
11.2 解: 过点D作DF⊥AB于点F.
∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DE=DF.
∵AB·DF+BC·DE=S△ABC,
∴×5×DE+×7×DE=12,
解得DE=2.
12.①②④ 解: ①∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠BAC的平分线上,∠ARP=∠ASP=90°.
∴∠SAP=∠RAP.
又∵AP=AP,
∴△APR≌△APS.(AAS)
∴AR=AS.故①正确.
②∵AQ=PQ,∴∠QAP=∠QPA.
∵∠QAP=∠BAP,
∴∠QPA=∠BAP.
∴QP∥AR.故②正确.
③在Rt△BRP和Rt△QSP中,只有PR=PS,
不满足判定三角形全等的条件,故③错误.
④∵△APR≌△APS,
∴AR=AS,PQ=PS,
∴AP垂直平分RS.故④正确.
13.解:∵CD为Rt△ABC斜边AB上的高,FG⊥AB,
∴CD∥FG.∴∠GFE=∠FEC.
∵AF是∠BAC的平分线,
∴∠CAF=∠BAF.
又∵∠ACB是直角,FG⊥AB,
∴∠GFE=∠CFE.
∴∠CFE=∠FEC.
∴CE=CF.
∵AF是∠BAC的平分线,∠ACB是直角,FG⊥AB,
∴FG=CF.∴CE=FG.
∵△ABF的面积为8,AB=8,
∴FG=2.
∴CE=2.
14.解:(1)证明:∵BD,CE是△ABC的高,
∴∠BDC=∠CEB=90°.
∵OB=OC,∴∠OBC=∠OCB.
又∵BC=CB,∴△BEC≌△CDB.
∴∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:∵△BEC≌△CDB,∴CE=BD.
又∵OB=OC,∴OD=OE.
又∵OD⊥AC,OE⊥AB,
∴点O在∠BAC的平分线上.
15.解:(1)CF=CG,OF=OG
(2)CF=CG.
证明:如图,过点C作CM⊥OA于点M,CN⊥OB于点N,
∴∠CMF=∠CNG=90°.
∵OC平分∠AOB,∠AOB=120°,
∴CM=CN,∠AOC=∠BOC=∠DCE=60°,
∠MCN=360°-∠AOB-∠CMF-∠CNO=60°.
∴∠DCE=∠MCN.
∴∠MCN-∠FCN=∠DCE-∠FCN,
即∠1=∠2.
在△CMF与△CNG中,∵
∴△CMF≌△CNG.∴CF=CG.
