沪科版数学八年级上册12.2 第3课时 一次函数的性质 同步课时练习(word版 含解析)
文档属性
| 名称 | 沪科版数学八年级上册12.2 第3课时 一次函数的性质 同步课时练习(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 244.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

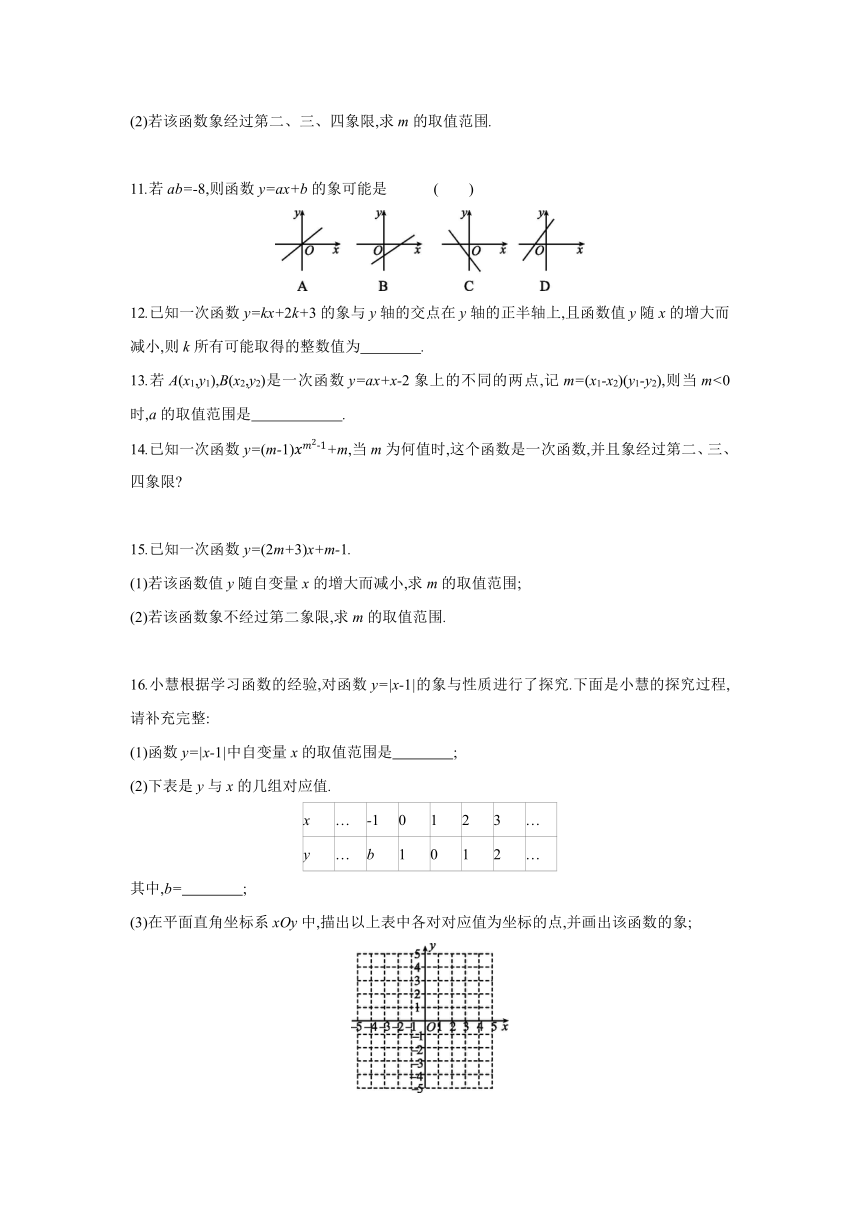
文档简介
第3课时 一次函数的性质
知识点 1 一次函数y随x的变化情况
1.已知正比例函数y=kx,当k>0时,函数象过原点且经过第一、三象限,自左向右是上升的,一次函数y=kx+b的象是由函数y=kx的象沿y轴上下平移得到的.由此可知,一次函数y=3x+1的象自左向右呈 趋势,说明y随x的增大而 .
2.直线y=-3x自左向右呈 趋势,函数的象与函数y=-3x的象是互相平行的,所以函数中,y随x的增大而 .
3.[2020·潜山期末] 下列一次函数中,y的值随着x值的增大而减小的是 ( )
A.y=x-1 B.y=x+2
C.y=-1+2x D.y=1-3x
4.[教材练习第2题变式题] 已知一次函数y=(1-3k)x+2k-1,试回答:
(1)当k为何值时,y随x的增大而减小
(2)当k为何值时,y随x的增大而增大
知识点 2 函数值的大小比较
5.已知M(1,a)和N(2,b)是一次函数y=-2x+1象上的两点,则a与b的大小关系是 (用“>”连接).
6.[教材练习第3题变式题] 在平面直角坐标系中,已知一次函数y=2x+1的象经过P1(x1,y1),P2(x2,y2)两点,若x1”“<”或“=”)
7.已知A(-3,y1),B(1,y2)是函数y=kx+b(k≠0)象上的两点,要使y1>y2,写出一个符合题意的k值: .
知识点 3 一次函数象的位置与系数的关系
8.一次函数y=kx+b的象是由一次函数y=kx的象平移得到的.因为一次函数y=2x的象是经过第一、三象限上升的直线,所以直线y=2x-3经过第 象限,同理,直线y=2x+3经过第 象限.
9.[2019·成都] 已知一次函数y=(k-3)x+1的象经过第一、二、四象限,则k的取值范围是 .
10.[教材练习第5题变式题] 已知关于x的一次函数y=(3-m)x+m-5.
(1)若它的象经过原点,求m的值,此时函数象经过哪些象限
(2)若该函数象经过第二、三、四象限,求m的取值范围.
11.若ab=-8,则函数y=ax+b的象可能是 ( )
12.已知一次函数y=kx+2k+3的象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所有可能取得的整数值为 .
13.若A(x1,y1),B(x2,y2)是一次函数y=ax+x-2象上的不同的两点,记m=(x1-x2)(y1-y2),则当m<0时,a的取值范围是 .
14.已知一次函数y=(m-1)+m,当m为何值时,这个函数是一次函数,并且象经过第二、三、四象限
15.已知一次函数y=(2m+3)x+m-1.
(1)若该函数值y随自变量x的增大而减小,求m的取值范围;
(2)若该函数象不经过第二象限,求m的取值范围.
16.小慧根据学习函数的经验,对函数y=|x-1|的象与性质进行了探究.下面是小慧的探究过程,请补充完整:
(1)函数y=|x-1|中自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x … -1 0 1 2 3 …
y … b 1 0 1 2 …
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的象;
(4)写出该函数的一条性质.
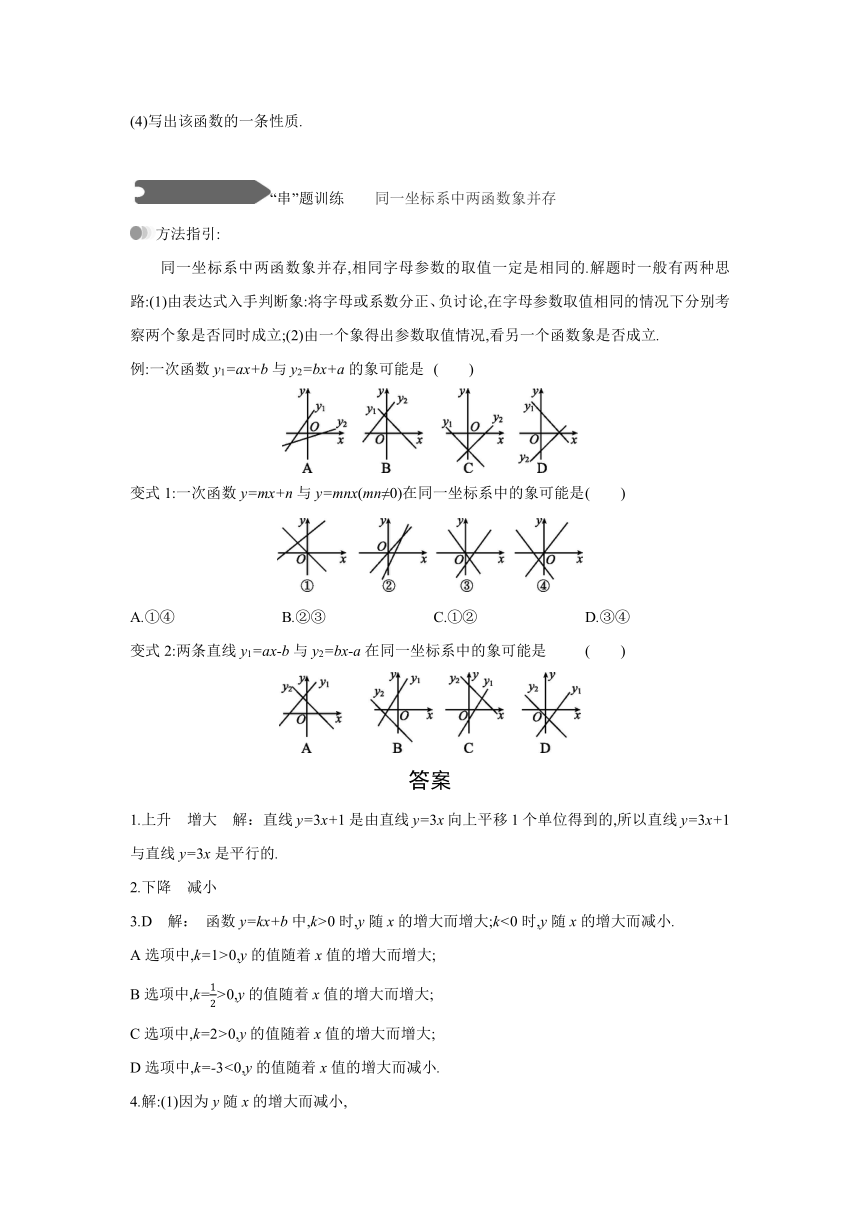
“串”题训练 同一坐标系中两函数象并存
方法指引:
同一坐标系中两函数象并存,相同字母参数的取值一定是相同的.解题时一般有两种思路:(1)由表达式入手判断象:将字母或系数分正、负讨论,在字母参数取值相同的情况下分别考察两个象是否同时成立;(2)由一个象得出参数取值情况,看另一个函数象是否成立.
例:一次函数y1=ax+b与y2=bx+a的象可能是 ( )
变式1:一次函数y=mx+n与y=mnx(mn≠0)在同一坐标系中的象可能是 ( )
A.①④ B.②③ C.①② D.③④
变式2:两条直线y1=ax-b与y2=bx-a在同一坐标系中的象可能是 ( )
答案
1.上升 增大 解: 直线y=3x+1是由直线y=3x向上平移1个单位得到的,所以直线y=3x+1与直线y=3x是平行的.
2.下降 减小
3.D 解: 函数y=kx+b中,k>0时,y随x的增大而增大;k<0时,y随x的增大而减小.
A选项中,k=1>0,y的值随着x值的增大而增大;
B选项中,k=>0,y的值随着x值的增大而增大;
C选项中,k=2>0,y的值随着x值的增大而增大;
D选项中,k=-3<0,y的值随着x值的增大而减小.
4.解:(1)因为y随x的增大而减小,
所以1-3k<0,解得k>.
(2)因为y随x的增大而增大,
所以1-3k>0,解得k<.
5.a>b 解: 方法一:把点M(1,a)和点N(2,b)分别代入函数y=-2x+1,求得a=-1,b=-3,所以a>b;方法二:画出象,根据象,显然得a>b;方法三:根据一次函数的性质,因为k=-2<0,所以函数值y随x的增大而减小,可得a>b.
6.< 解: 因为k=2>0,所以y随x的增大而增大.又因为x17.答案不唯一,如图-2 解: 因为-3<1,而y1>y2,所以y随x的增大而减小,所以k<0.
8.一、三、四 一、二、三
9.k<3 解: 因为一次函数y=(k-3)x+1的象经过第一、二、四象限,所以k-3<0,解得k<3.
10.解:(1)由于此函数的象经过原点,故m-5=0且3-m≠0,解得m=5.
所以此函数的表达式为y=-2x,此时函数象经过第二、四象限.
(2)由该函数象经过第二、三、四象限,可得
解得311.B 解: 根据ab=-8,判断出当a>0时,b<0,或当a<0时,b>0.选项A中,b=0,不符合题意;选项B中,a>0,b<0,符合题意;选项C中,a<0,b<0,不符合题意;选项D中,a>0,b>0,不符合题意.
12.-1 解: 由题意,得
解得-13.a<-1 解: 因为A(x1,y1),B(x2,y2)是一次函数y=ax+x-2=(a+1)x-2象上的不同的两点,m=(x1-x2)(y1-y2)<0,所以函数值y随x的增大而减小.所以a+1<0,解得a<-1.
14.解: 要使函数y=(m-1)+m为一次函数,则要求解得m=±.
当m=时,m-1=-1>0,函数象经过第一、二、三象限;
当m=-时-1<0,函数象经过第二、三、四象限.
综上可知,当m=-时,这个函数是一次函数,并且象经过第二、三、四象限.
15.解:(1)因为函数值y随自变量x的增大而减小,
所以2m+3<0,
解得m<-.
(2)因为该函数象不经过第二象限,
所以
解得-16.解:(1)因为x无论为何值,函数均有意义,
所以x为任意实数.故答案为任意实数.
(2)因为当x=-1时,y=2,
所以b=2.故答案为2.
(3)如图所示.
(4)由函数象可知,函数的最小值为0(答案不唯一).
“串”题训练
例:D 解: 方法一:
(1)当a>0,b>0时,两条直线都经过第一、二、三象限,没有选项相符;
(2)当a<0,b<0时,两条直线都经过第二、三、四象限,没有选项相符;
(3)当a>0,b<0,或a<0,b>0时,一条直线经过第一、三、四象限,另一条直线经过第一、二、四象限,只有D选项符合.
方法二:A选项,由直线y1可知,a>0,b>0;由直线y2可知a<0,矛盾;
B选项,由直线y1可知,a<0,b>0;由直线y2可知a>0,矛盾;
C选项,由直线y1可知,a<0,b<0;由直线y2可知b>0,矛盾;
D选项,由直线y1可知,a<0,b>0,;由直线y2可知a<0,b>0,两者相符.故选D.
变式1:D 解: 当mn>0时,m,n同号.
同正时,直线y=mx+n经过第一、二、三象限;
同负时,直线y=mx+n经过第二、三、四象限.
故④正确.
当mn<0时,m,n异号.
m>0,n<0时,直线y=mx+n经过第一、三、四象限;
m<0,n>0时,直线y=mx+n经过第一、二、四象限.
故③正确.
变式2:B 解: A选项,直线y1经过第一、二、三象限,则a>0,b<0,直线y2经过第一、二、四象限,则b<0,a<0,前后矛盾,故A选项错误;
B选项,直线y1经过第一、二、三象限,则a>0,b<0,直线y2经过第二、三、四象限,则b<0,a>0,故B选项正确;
C选项,直线y1经过第一、三、四象限,则a>0,b>0,直线y2经过第一、二、四象限,则b<0,a<0,前后矛盾,故C选项错误;
D选项,直线y1经过第一、三、四象限,则a>0,b>0,直线y2经过第二、三、四象限,则b<0,a>0,前后矛盾,故D选项错误.
知识点 1 一次函数y随x的变化情况
1.已知正比例函数y=kx,当k>0时,函数象过原点且经过第一、三象限,自左向右是上升的,一次函数y=kx+b的象是由函数y=kx的象沿y轴上下平移得到的.由此可知,一次函数y=3x+1的象自左向右呈 趋势,说明y随x的增大而 .
2.直线y=-3x自左向右呈 趋势,函数的象与函数y=-3x的象是互相平行的,所以函数中,y随x的增大而 .
3.[2020·潜山期末] 下列一次函数中,y的值随着x值的增大而减小的是 ( )
A.y=x-1 B.y=x+2
C.y=-1+2x D.y=1-3x
4.[教材练习第2题变式题] 已知一次函数y=(1-3k)x+2k-1,试回答:
(1)当k为何值时,y随x的增大而减小
(2)当k为何值时,y随x的增大而增大
知识点 2 函数值的大小比较
5.已知M(1,a)和N(2,b)是一次函数y=-2x+1象上的两点,则a与b的大小关系是 (用“>”连接).
6.[教材练习第3题变式题] 在平面直角坐标系中,已知一次函数y=2x+1的象经过P1(x1,y1),P2(x2,y2)两点,若x1
7.已知A(-3,y1),B(1,y2)是函数y=kx+b(k≠0)象上的两点,要使y1>y2,写出一个符合题意的k值: .
知识点 3 一次函数象的位置与系数的关系
8.一次函数y=kx+b的象是由一次函数y=kx的象平移得到的.因为一次函数y=2x的象是经过第一、三象限上升的直线,所以直线y=2x-3经过第 象限,同理,直线y=2x+3经过第 象限.
9.[2019·成都] 已知一次函数y=(k-3)x+1的象经过第一、二、四象限,则k的取值范围是 .
10.[教材练习第5题变式题] 已知关于x的一次函数y=(3-m)x+m-5.
(1)若它的象经过原点,求m的值,此时函数象经过哪些象限
(2)若该函数象经过第二、三、四象限,求m的取值范围.
11.若ab=-8,则函数y=ax+b的象可能是 ( )
12.已知一次函数y=kx+2k+3的象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所有可能取得的整数值为 .
13.若A(x1,y1),B(x2,y2)是一次函数y=ax+x-2象上的不同的两点,记m=(x1-x2)(y1-y2),则当m<0时,a的取值范围是 .
14.已知一次函数y=(m-1)+m,当m为何值时,这个函数是一次函数,并且象经过第二、三、四象限
15.已知一次函数y=(2m+3)x+m-1.
(1)若该函数值y随自变量x的增大而减小,求m的取值范围;
(2)若该函数象不经过第二象限,求m的取值范围.
16.小慧根据学习函数的经验,对函数y=|x-1|的象与性质进行了探究.下面是小慧的探究过程,请补充完整:
(1)函数y=|x-1|中自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x … -1 0 1 2 3 …
y … b 1 0 1 2 …
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的象;
(4)写出该函数的一条性质.
“串”题训练 同一坐标系中两函数象并存
方法指引:
同一坐标系中两函数象并存,相同字母参数的取值一定是相同的.解题时一般有两种思路:(1)由表达式入手判断象:将字母或系数分正、负讨论,在字母参数取值相同的情况下分别考察两个象是否同时成立;(2)由一个象得出参数取值情况,看另一个函数象是否成立.
例:一次函数y1=ax+b与y2=bx+a的象可能是 ( )
变式1:一次函数y=mx+n与y=mnx(mn≠0)在同一坐标系中的象可能是 ( )
A.①④ B.②③ C.①② D.③④
变式2:两条直线y1=ax-b与y2=bx-a在同一坐标系中的象可能是 ( )
答案
1.上升 增大 解: 直线y=3x+1是由直线y=3x向上平移1个单位得到的,所以直线y=3x+1与直线y=3x是平行的.
2.下降 减小
3.D 解: 函数y=kx+b中,k>0时,y随x的增大而增大;k<0时,y随x的增大而减小.
A选项中,k=1>0,y的值随着x值的增大而增大;
B选项中,k=>0,y的值随着x值的增大而增大;
C选项中,k=2>0,y的值随着x值的增大而增大;
D选项中,k=-3<0,y的值随着x值的增大而减小.
4.解:(1)因为y随x的增大而减小,
所以1-3k<0,解得k>.
(2)因为y随x的增大而增大,
所以1-3k>0,解得k<.
5.a>b 解: 方法一:把点M(1,a)和点N(2,b)分别代入函数y=-2x+1,求得a=-1,b=-3,所以a>b;方法二:画出象,根据象,显然得a>b;方法三:根据一次函数的性质,因为k=-2<0,所以函数值y随x的增大而减小,可得a>b.
6.< 解: 因为k=2>0,所以y随x的增大而增大.又因为x1
8.一、三、四 一、二、三
9.k<3 解: 因为一次函数y=(k-3)x+1的象经过第一、二、四象限,所以k-3<0,解得k<3.
10.解:(1)由于此函数的象经过原点,故m-5=0且3-m≠0,解得m=5.
所以此函数的表达式为y=-2x,此时函数象经过第二、四象限.
(2)由该函数象经过第二、三、四象限,可得
解得3
12.-1 解: 由题意,得
解得-
14.解: 要使函数y=(m-1)+m为一次函数,则要求解得m=±.
当m=时,m-1=-1>0,函数象经过第一、二、三象限;
当m=-时-1<0,函数象经过第二、三、四象限.
综上可知,当m=-时,这个函数是一次函数,并且象经过第二、三、四象限.
15.解:(1)因为函数值y随自变量x的增大而减小,
所以2m+3<0,
解得m<-.
(2)因为该函数象不经过第二象限,
所以
解得-
所以x为任意实数.故答案为任意实数.
(2)因为当x=-1时,y=2,
所以b=2.故答案为2.
(3)如图所示.
(4)由函数象可知,函数的最小值为0(答案不唯一).
“串”题训练
例:D 解: 方法一:
(1)当a>0,b>0时,两条直线都经过第一、二、三象限,没有选项相符;
(2)当a<0,b<0时,两条直线都经过第二、三、四象限,没有选项相符;
(3)当a>0,b<0,或a<0,b>0时,一条直线经过第一、三、四象限,另一条直线经过第一、二、四象限,只有D选项符合.
方法二:A选项,由直线y1可知,a>0,b>0;由直线y2可知a<0,矛盾;
B选项,由直线y1可知,a<0,b>0;由直线y2可知a>0,矛盾;
C选项,由直线y1可知,a<0,b<0;由直线y2可知b>0,矛盾;
D选项,由直线y1可知,a<0,b>0,;由直线y2可知a<0,b>0,两者相符.故选D.
变式1:D 解: 当mn>0时,m,n同号.
同正时,直线y=mx+n经过第一、二、三象限;
同负时,直线y=mx+n经过第二、三、四象限.
故④正确.
当mn<0时,m,n异号.
m>0,n<0时,直线y=mx+n经过第一、三、四象限;
m<0,n>0时,直线y=mx+n经过第一、二、四象限.
故③正确.
变式2:B 解: A选项,直线y1经过第一、二、三象限,则a>0,b<0,直线y2经过第一、二、四象限,则b<0,a<0,前后矛盾,故A选项错误;
B选项,直线y1经过第一、二、三象限,则a>0,b<0,直线y2经过第二、三、四象限,则b<0,a>0,故B选项正确;
C选项,直线y1经过第一、三、四象限,则a>0,b>0,直线y2经过第一、二、四象限,则b<0,a<0,前后矛盾,故C选项错误;
D选项,直线y1经过第一、三、四象限,则a>0,b>0,直线y2经过第二、三、四象限,则b<0,a>0,前后矛盾,故D选项错误.
