沪科版数学八年级上册12.2 第6课时 一次函数的简单应用——双一次函数图象问题 同步课时练习(word版 含解析)
文档属性
| 名称 | 沪科版数学八年级上册12.2 第6课时 一次函数的简单应用——双一次函数图象问题 同步课时练习(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 208.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 16:40:09 | ||
图片预览


文档简介
第6课时 一次函数的简单应用—双一次函数象问题
知识点 1 双一次函数的简单应用
1.电信局规定了拨号入网的两种收费方式,一是有月租费:y1=0.02x+60,二是无月租费:y2=0.05x.其中y1(元),y2(元)分别是两种上网方式付费钱数,x(分)是上网时间.当y12000时,选择 合算;当y1>y2,即上网时间 时,选择无月租费的合算.
2.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如图下优惠:
会员年卡类型 办卡费用(元) 每次游泳收费(元)
A类 50 25
B类 400 15
例如图:购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元).若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡
B.购买B类会员年卡
C.购买A类或B类都可以
D.不购买会员年卡
3.[教材例6变式题] 五一快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方案,甲旅行社的优惠方案是买4张全票,其余人按半价优惠;乙旅行社的优惠方案是一律按7折优惠,已知两家旅行社的原价均为每人100元.(旅游人数超过4人)
(1)分别表示出甲旅行社收费y1(元)、乙旅行社收费y2(元)与旅游人数x(人)之间的函数表达式;
(2)就参加旅游的人数讨论哪家旅行社的收费更优惠.
知识点 2 双一次函数象的综合应用
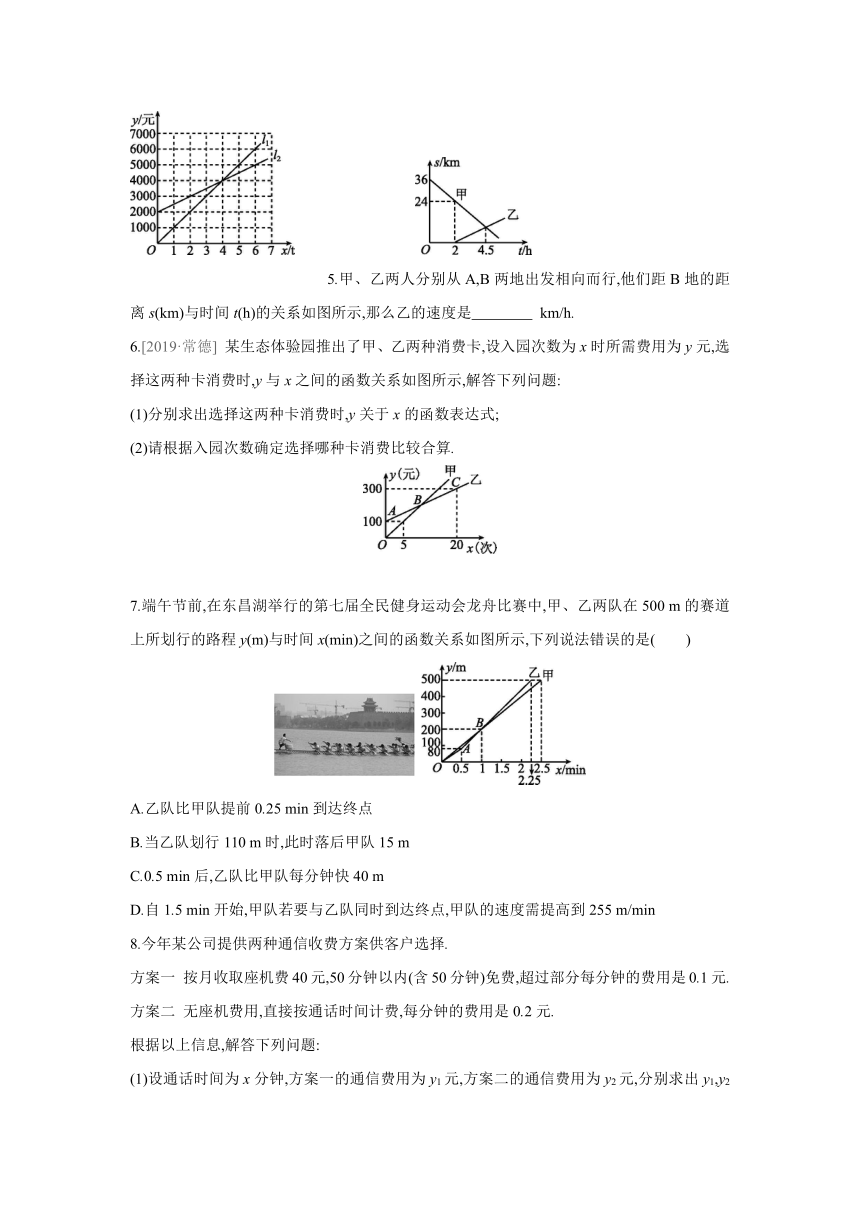
4.如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量 ( )
A.小于3 t B.大于3 t
C.小于4 t D.大于4 t
5.甲、乙两人分别从A,B两地出发相向而行,他们距B地的距离s(km)与时间t(h)的关系如图所示,那么乙的速度是 km/h.
6.[2019·常德] 某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x之间的函数关系如图所示,解答下列问题:
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
7.端午节前,在东昌湖举行的第七届全民健身运动会龙舟比赛中,甲、乙两队在500 m的赛道上所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法错误的是( )
A.乙队比甲队提前0.25 min到达终点
B.当乙队划行110 m时,此时落后甲队15 m
C.0.5 min后,乙队比甲队每分钟快40 m
D.自1.5 min开始,甲队若要与乙队同时到达终点,甲队的速度需提高到255 m/min
8.今年某公司提供两种通信收费方案供客户选择.
方案一 按月收取座机费40元,50分钟以内(含50分钟)免费,超过部分每分钟的费用是0.1元.
方案二 无座机费用,直接按通话时间计费,每分钟的费用是0.2元.
根据以上信息,解答下列问题:
(1)设通话时间为x分钟,方案一的通信费用为y1元,方案二的通信费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你通过计算说明如图何选用通信收费方案更合算;
(3)小明的爸爸每月的通话时间约为500分钟,应选用哪种通信收费方案.
9.[2020·合肥包河区期末] 如图①,A,B两地相距60 km,甲从A地去B地,乙从B地去A地,②中l1,l2分别表示甲、乙两人离B地的距离y(km)与甲出发的时间x(h)之间的函数关系象.
(1)根据象,直接写出乙的行驶速度是 ;
(2)解释交点A的实际意义;
(3)甲出发多长时间,两人之间的距离恰好相距5 km;
(4)若用y3(km)表示甲、乙两人之间的距离,请建立平面直角坐标系画出y3(km)关于时间x(h)的函数关系象,并注明关键点的数据.
答案
1.有月租费的 0≤x<2000
2.B
3.解:(1)根据题意,得y1=100×4+100×(x-4)=50x+200;
y2=100×70%x=70x.
(2)当y110,
所以旅游的人数超过10人时,甲旅行社收费更优惠;
当y1=y2时,即50x+200=70x,解得x=10,
所以旅游的人数为10人时,甲、乙旅行社收费一样;
当y1>y2时,即50x+200>70x,解得x<10,
所以旅游的人数超过4人但少于10人时,乙旅行社收费更优惠.
综上所述,当旅游的人数超过4人但少于10人时,乙旅行社收费更优惠;当旅游的人数为10人时,甲、乙旅行社收费一样;当旅游的人数超过10人时,甲旅行社收费更优惠.
4.D 解: 观察象可知当销售量大于4 t时,销售收入大于销售成本.故选D.
5.3.6
6.解:(1)设y甲=k1x.根据题意,得5k1=100,
解得k1=20,所以y甲=20x.
设y乙=k2x+100.
根据题意,得20k2+100=300,
解得k2=10,所以y乙=10x+100.
(2)令y甲=y乙,即20x=10x+100,
解得x=10,即B点的横坐标是10.
由题可知当x<10时,y甲故当入园次数小于10次时,选择甲消费卡比较合算;
当入园次数等于10次时,选择两种消费卡费用一样多;
当入园次数大于10次时,选择乙消费卡比较合算.
7.D 解: 由象可知甲队到达终点用时2.5 min,乙队到达终点用时2.25 min,所以乙队比甲队提前0.25 min到达终点,A选项正确,不符合题意;由象可求出甲队所划行的路程与时间的函数表达式为y=200x(0≤x≤2.5),乙队所划行的路程与时间的函数表达式为y=
当乙队划行110 m时,可求出乙队所用时间为 min,把x=代入甲队的表达式可得y=125,所以当乙队划行110 m时,此时落后甲队15 m,B选项正确;由象可知0.5 min后,乙队速度为240 m/min,甲队速度为200 m/min,所以C选项正确;由排除法可知选D.
8.解:(1)根据题意知,当0≤x≤50时,y1=40.
当x>50时,y1=40+(x-50)×0.1=35+0.1x.
故y1=
y2=0.2x(x≥0).
(2)当0≤x≤50时,y1=40>y2,
选择方案二合算.
当x>50时,
①若y1>y2,即0.1x+35>0.2x,
解得x<350,选择方案二合算;
②若y1=y2,即0.1x+35=0.2x,
解得x=350,选择两种方案一样合算;
③若y1解得x>350,选择方案一合算.
综上所述,当通话时间小于350分钟时,选择方案二合算;当通话时间为350分钟时,选择两种方案一样合算;当通话时间大于350分钟时,选择方案一合算.
(3)由于500>350,所以小明的爸爸选用通信收费方案一合算.
9.解:(1)20 km/h
(2)设直线l1的函数表达式为y1=k1x+b1.
由题意,得解得
即直线l1的函数表达式为y1=-30x+60.
设直线l2的函数表达式为y2=k2x+b2.
由题意,得解得
即直线l2的函数表达式为y2=20x-10.
联立解得
即点A的坐标为(1.4,18),
所以点A的实际意义是在甲出发1.4 h时,甲、乙两人相遇,此时距离B地18 km.
(3)由题意可得,|(-30x+60)-(20x-10)|=5,
解得x1=1.3,x2=1.5.
答:当甲出发1.3 h或1.5 h时,两人之间的距离恰好相距5 km.
(4)由题意可得,
当0≤x≤0.5时,y3=-30x+60;
当0.5当1.4当2所以y3(km)关于时间x(h)的函数关系象如图所示.
知识点 1 双一次函数的简单应用
1.电信局规定了拨号入网的两种收费方式,一是有月租费:y1=0.02x+60,二是无月租费:y2=0.05x.其中y1(元),y2(元)分别是两种上网方式付费钱数,x(分)是上网时间.当y1
2.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如图下优惠:
会员年卡类型 办卡费用(元) 每次游泳收费(元)
A类 50 25
B类 400 15
例如图:购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元).若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡
B.购买B类会员年卡
C.购买A类或B类都可以
D.不购买会员年卡
3.[教材例6变式题] 五一快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方案,甲旅行社的优惠方案是买4张全票,其余人按半价优惠;乙旅行社的优惠方案是一律按7折优惠,已知两家旅行社的原价均为每人100元.(旅游人数超过4人)
(1)分别表示出甲旅行社收费y1(元)、乙旅行社收费y2(元)与旅游人数x(人)之间的函数表达式;
(2)就参加旅游的人数讨论哪家旅行社的收费更优惠.
知识点 2 双一次函数象的综合应用
4.如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量 ( )
A.小于3 t B.大于3 t
C.小于4 t D.大于4 t
5.甲、乙两人分别从A,B两地出发相向而行,他们距B地的距离s(km)与时间t(h)的关系如图所示,那么乙的速度是 km/h.
6.[2019·常德] 某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x之间的函数关系如图所示,解答下列问题:
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
7.端午节前,在东昌湖举行的第七届全民健身运动会龙舟比赛中,甲、乙两队在500 m的赛道上所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法错误的是( )
A.乙队比甲队提前0.25 min到达终点
B.当乙队划行110 m时,此时落后甲队15 m
C.0.5 min后,乙队比甲队每分钟快40 m
D.自1.5 min开始,甲队若要与乙队同时到达终点,甲队的速度需提高到255 m/min
8.今年某公司提供两种通信收费方案供客户选择.
方案一 按月收取座机费40元,50分钟以内(含50分钟)免费,超过部分每分钟的费用是0.1元.
方案二 无座机费用,直接按通话时间计费,每分钟的费用是0.2元.
根据以上信息,解答下列问题:
(1)设通话时间为x分钟,方案一的通信费用为y1元,方案二的通信费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你通过计算说明如图何选用通信收费方案更合算;
(3)小明的爸爸每月的通话时间约为500分钟,应选用哪种通信收费方案.
9.[2020·合肥包河区期末] 如图①,A,B两地相距60 km,甲从A地去B地,乙从B地去A地,②中l1,l2分别表示甲、乙两人离B地的距离y(km)与甲出发的时间x(h)之间的函数关系象.
(1)根据象,直接写出乙的行驶速度是 ;
(2)解释交点A的实际意义;
(3)甲出发多长时间,两人之间的距离恰好相距5 km;
(4)若用y3(km)表示甲、乙两人之间的距离,请建立平面直角坐标系画出y3(km)关于时间x(h)的函数关系象,并注明关键点的数据.
答案
1.有月租费的 0≤x<2000
2.B
3.解:(1)根据题意,得y1=100×4+100×(x-4)=50x+200;
y2=100×70%x=70x.
(2)当y1
所以旅游的人数超过10人时,甲旅行社收费更优惠;
当y1=y2时,即50x+200=70x,解得x=10,
所以旅游的人数为10人时,甲、乙旅行社收费一样;
当y1>y2时,即50x+200>70x,解得x<10,
所以旅游的人数超过4人但少于10人时,乙旅行社收费更优惠.
综上所述,当旅游的人数超过4人但少于10人时,乙旅行社收费更优惠;当旅游的人数为10人时,甲、乙旅行社收费一样;当旅游的人数超过10人时,甲旅行社收费更优惠.
4.D 解: 观察象可知当销售量大于4 t时,销售收入大于销售成本.故选D.
5.3.6
6.解:(1)设y甲=k1x.根据题意,得5k1=100,
解得k1=20,所以y甲=20x.
设y乙=k2x+100.
根据题意,得20k2+100=300,
解得k2=10,所以y乙=10x+100.
(2)令y甲=y乙,即20x=10x+100,
解得x=10,即B点的横坐标是10.
由题可知当x<10时,y甲
当入园次数等于10次时,选择两种消费卡费用一样多;
当入园次数大于10次时,选择乙消费卡比较合算.
7.D 解: 由象可知甲队到达终点用时2.5 min,乙队到达终点用时2.25 min,所以乙队比甲队提前0.25 min到达终点,A选项正确,不符合题意;由象可求出甲队所划行的路程与时间的函数表达式为y=200x(0≤x≤2.5),乙队所划行的路程与时间的函数表达式为y=
当乙队划行110 m时,可求出乙队所用时间为 min,把x=代入甲队的表达式可得y=125,所以当乙队划行110 m时,此时落后甲队15 m,B选项正确;由象可知0.5 min后,乙队速度为240 m/min,甲队速度为200 m/min,所以C选项正确;由排除法可知选D.
8.解:(1)根据题意知,当0≤x≤50时,y1=40.
当x>50时,y1=40+(x-50)×0.1=35+0.1x.
故y1=
y2=0.2x(x≥0).
(2)当0≤x≤50时,y1=40>y2,
选择方案二合算.
当x>50时,
①若y1>y2,即0.1x+35>0.2x,
解得x<350,选择方案二合算;
②若y1=y2,即0.1x+35=0.2x,
解得x=350,选择两种方案一样合算;
③若y1
综上所述,当通话时间小于350分钟时,选择方案二合算;当通话时间为350分钟时,选择两种方案一样合算;当通话时间大于350分钟时,选择方案一合算.
(3)由于500>350,所以小明的爸爸选用通信收费方案一合算.
9.解:(1)20 km/h
(2)设直线l1的函数表达式为y1=k1x+b1.
由题意,得解得
即直线l1的函数表达式为y1=-30x+60.
设直线l2的函数表达式为y2=k2x+b2.
由题意,得解得
即直线l2的函数表达式为y2=20x-10.
联立解得
即点A的坐标为(1.4,18),
所以点A的实际意义是在甲出发1.4 h时,甲、乙两人相遇,此时距离B地18 km.
(3)由题意可得,|(-30x+60)-(20x-10)|=5,
解得x1=1.3,x2=1.5.
答:当甲出发1.3 h或1.5 h时,两人之间的距离恰好相距5 km.
(4)由题意可得,
当0≤x≤0.5时,y3=-30x+60;
当0.5
