沪科版数学八年级上册同步课时练习:13.1.1 三角形中边的关系(word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步课时练习:13.1.1 三角形中边的关系(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 98.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 16:41:42 | ||
图片预览



文档简介
13.1 第1课时 三角形中边的关系
知识点 1 三角形的概念
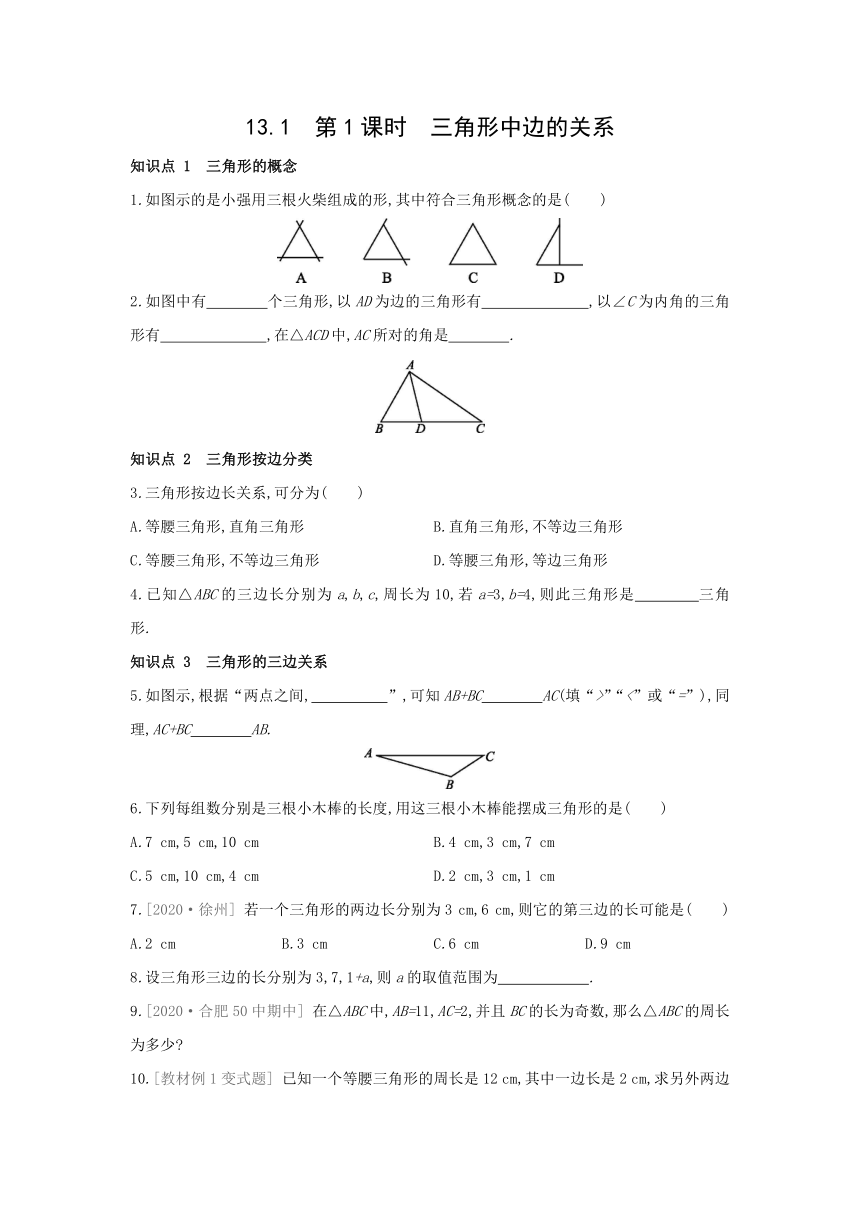
1.如图示的是小强用三根火柴组成的形,其中符合三角形概念的是( )
2.如图中有 个三角形,以AD为边的三角形有 ,以∠C为内角的三角形有 ,在△ACD中,AC所对的角是 .
知识点 2 三角形按边分类
3.三角形按边长关系,可分为( )
A.等腰三角形,直角三角形 B.直角三角形,不等边三角形
C.等腰三角形,不等边三角形 D.等腰三角形,等边三角形
4.已知△ABC的三边长分别为a,b,c,周长为10,若a=3,b=4,则此三角形是 三角形.
知识点 3 三角形的三边关系
5.如图示,根据“两点之间, ”,可知AB+BC AC(填“>”“<”或“=”),同理,AC+BC AB.
6.下列每组数分别是三根小木棒的长度,用这三根小木棒能摆成三角形的是( )
A.7 cm,5 cm,10 cm B.4 cm,3 cm,7 cm
C.5 cm,10 cm,4 cm D.2 cm,3 cm,1 cm
7.[2020·徐州] 若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( )
A.2 cm B.3 cm C.6 cm D.9 cm
8.设三角形三边的长分别为3,7,1+a,则a的取值范围为 .
9.[2020·合肥50中期中] 在△ABC中,AB=11,AC=2,并且BC的长为奇数,那么△ABC的周长为多少
10.[教材例1变式题] 已知一个等腰三角形的周长是12 cm,其中一边长是2 cm,求另外两边的长.
11.已知a,b,c是△ABC的三条边长,化简|a结果为( )
A.2a+2b-2c B.2a+2b C.2c D.0
12.[2020·绍兴] 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4 B.5 C.6 D.7
13.已知一个三角形的三条边长均为正整数,若其中仅有一条边长为5,且它又不是最短边,则满足条件的三角形的个数为( )
A.4 B.6 C.8 D.10
14.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为整数,则c= .
15.有人说:“如图果△ABC的三边长a,b,c满足a2-b2=ac-bc,那么△ABC一定是等腰三角形.”你同意这个说法吗 请给出你的理由.
16.[2020·合肥瑶海区期中] 已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
17.(1)如图所示,D为△ABC的边AC上任意一点,连接BD,E为BD上任意一点,连接CE.
用不等号填空:
AB+AC DB+DC,
DB+DC EB+EC;
(2)如图所示,M,N是△ABC内任意两点,试探索AB+AC与BM+MN+NC之间的大小关系,并写出探究过程.
① ②
“串”题训练 等腰三角形分类讨论时不能忽略三边关系
方法指引:
等腰三角形已知两边长求周长时,腰长与底边长需要分类讨论,每种情况都要验证是否能够构成三角形.
例:已知等腰三角形ABC的两边长a和b满足(a-6)2+=0,求△ABC的周长.
变式1:若一条长为31 cm的细线能围成一边长等于7 cm的等腰三角形,则该等腰三角形的腰长为( )
A.7 cm B.9 cm C.7 cm或12 cm D.12 cm
变式2:已知等腰三角形的一边长是3,另一边长是方程+=1的解,则这个三角形的周长
是( )
A.10 B.11 C.10或11 D.7或8
变式3:在△ABC中,AB=8,且BC=2a+2,AC=22.
(1)求a的取值范围;
(2)若△ABC为等腰三角形,求这个三角形的周长.
答案
1.C
2.3 △ABD,△ACD △ACD,△ACB ∠ADC
3.C
4.等腰 解: 因为a+b+c=10,a=3,b=4,所以c=3,即a=c,所以△ABC为等腰三角形.
[点评] 要判断三角形的形状,可先通过计算得出三角形的三条边长,再比较各边长,判断其形状.
5.线段最短 > >
6.A 解: A项,5+7=12>10,能摆成三角形;
B项,3+4=7,不能摆成三角形;
C项,4+5=9<10,不能摆成三角形;
D项,1+2=3,不能摆成三角形.故选A.
7.C 解: 设第三边长为x cm,根据三角形的三边关系可得6-38.3故答案为39.解:设BC的长为x.根据三角形的三边关系,得
11-2即9因为x为奇数,所以x=11,
所以△ABC的周长为11+11+2=24.
10.解:若该等腰三角形的腰长为2 cm,则另外两边的长分别为2 cm,8 cm,根据三角形三边关系知不能构成三角形;
若等腰三角形的底边长为2 cm,则腰长为×(12-2)=5(cm),即另外两边的长分别为5 cm,5 cm.
综上,该等腰三角形的另外两边的长分别为5 cm,5 cm.
11.D 解: 根据三角形三边满足的条件:两边的和大于第三边,两边的差小于第三边,即可确定a+b-c>00,所以|aa+b-c0.故选D.
12.B 解: ①当长度分别为5,3,4时,能构成三角形,且最长边为5;
②当长度分别为2,6,4时,不能构成三角形;
③当长度分别为2,7,3时,不能构成三角形;
④当长度分别为6,3,3时,不能构成三角形.
综上所述,得到的三角形的最长边长为5.
13.D 解: 因为三条边长均为正整数,并且其中仅有一条边长为5,且它又不是最短边,所以:
①当5是最大的边长时,可能的情况有四种:4,2,5;4,3,5;4,4,5;3,3,5;
②当5是较大的边长时,可能的情况有六种:2,5,6;3,5,7;3,5,6;4,5,6;4,5,7;4,5,8.
综上,共十种情况,所以满足条件的三角形共有10个.
14.7 解: 因为a,b满足|a-7|+(b-1)2=0,所以a-7=0,b-1=0,解得a=7,b=1.因为615.解:同意.理由如图下:
因为a2-b2=ac-bc,
所以(a-b)(a+b)=c(a-b),
即(a-b)(a+b-c)=0.
因为a,b,c是△ABC的三边长,
所以a+b-c>0,
所以a-b=0,即a=b,
故△ABC为等腰三角形.
16.解:(1)因为(a-b)2+(b-c)2=0,
所以a-b=0,b-c=0,
所以a=b=c,
所以△ABC是等边三角形.
(2)因为a=5,b=2,且c为整数,
所以5-2即3所以c=4,5,6,
所以当c=4时,△ABC的周长有最小值,最小值为5+2+4=11;
当c=6时,△ABC的周长有最大值,最大值为5+2+6=13.
17.解:(1)> >
(2)AB+AC>BM+MN+NC.
延长BM交AC于点D,延长CN交BD于点E.
由(1)可得AB+AC>DB+DC>EB+EC,
即AB+AC>EM+BM+EN+NC=(EM+EN)+BM+NC>MN+BM+NC,
所以AB+AC>BM+MN+NC.
“串”题训练
例:解: 利用非负数的和为0,求出a=6,b=3,然后分情况讨论腰长为3或6,要考虑能不能构成三角形.
解:因为(a-6)2≥0,≥0,(a-6)2+=0,
所以
解得
若6为腰长,则△ABC的三边长分别为6,6,3,其周长为6+6+3=15;
若3为腰长,则此时△ABC的三边长分别为3,3,6,3+3=6,不能构成三角形.
综上所述,△ABC的周长为15.
变式1:D 解: 若腰长为7 cm,设底边长为x cm,则7+7+x=31,解得x=17,
此时三角形的三边长分别为7 cm,7 cm,17 cm.
因为7+7<17,
所以此三角形不成立;
若底边长为7 cm,设腰长为y cm.由题意,得
7+y+y=31,
解得y=12,
此时三角形的三边长分别为7 cm,12 cm,12 cm.
故选D.
变式2:C 解: +=1,解得x=4.
当等腰三角形的腰长为4,底边长为3时,这个三角形的周长为4+4+3=11;
当等腰三角形的腰长为3,底边长为4时,这个三角形的周长为4+3+3=10.
所以这个三角形的周长是10或11.
变式3:解:(1)由题意,得22-8<2a+2<22+8,
解得6(2)①若AB=BC,则三角形的三边长为8,8,22,由于8+8<22,因此以8,8,22为边长构不成三角形;
②若AC=BC,则三角形的三边长为8,22,22,此时三角形的周长为8+22+22=52.
综上所述,这个三角形的周长为52.
知识点 1 三角形的概念
1.如图示的是小强用三根火柴组成的形,其中符合三角形概念的是( )
2.如图中有 个三角形,以AD为边的三角形有 ,以∠C为内角的三角形有 ,在△ACD中,AC所对的角是 .
知识点 2 三角形按边分类
3.三角形按边长关系,可分为( )
A.等腰三角形,直角三角形 B.直角三角形,不等边三角形
C.等腰三角形,不等边三角形 D.等腰三角形,等边三角形
4.已知△ABC的三边长分别为a,b,c,周长为10,若a=3,b=4,则此三角形是 三角形.
知识点 3 三角形的三边关系
5.如图示,根据“两点之间, ”,可知AB+BC AC(填“>”“<”或“=”),同理,AC+BC AB.
6.下列每组数分别是三根小木棒的长度,用这三根小木棒能摆成三角形的是( )
A.7 cm,5 cm,10 cm B.4 cm,3 cm,7 cm
C.5 cm,10 cm,4 cm D.2 cm,3 cm,1 cm
7.[2020·徐州] 若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( )
A.2 cm B.3 cm C.6 cm D.9 cm
8.设三角形三边的长分别为3,7,1+a,则a的取值范围为 .
9.[2020·合肥50中期中] 在△ABC中,AB=11,AC=2,并且BC的长为奇数,那么△ABC的周长为多少
10.[教材例1变式题] 已知一个等腰三角形的周长是12 cm,其中一边长是2 cm,求另外两边的长.
11.已知a,b,c是△ABC的三条边长,化简|a结果为( )
A.2a+2b-2c B.2a+2b C.2c D.0
12.[2020·绍兴] 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4 B.5 C.6 D.7
13.已知一个三角形的三条边长均为正整数,若其中仅有一条边长为5,且它又不是最短边,则满足条件的三角形的个数为( )
A.4 B.6 C.8 D.10
14.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为整数,则c= .
15.有人说:“如图果△ABC的三边长a,b,c满足a2-b2=ac-bc,那么△ABC一定是等腰三角形.”你同意这个说法吗 请给出你的理由.
16.[2020·合肥瑶海区期中] 已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
17.(1)如图所示,D为△ABC的边AC上任意一点,连接BD,E为BD上任意一点,连接CE.
用不等号填空:
AB+AC DB+DC,
DB+DC EB+EC;
(2)如图所示,M,N是△ABC内任意两点,试探索AB+AC与BM+MN+NC之间的大小关系,并写出探究过程.
① ②
“串”题训练 等腰三角形分类讨论时不能忽略三边关系
方法指引:
等腰三角形已知两边长求周长时,腰长与底边长需要分类讨论,每种情况都要验证是否能够构成三角形.
例:已知等腰三角形ABC的两边长a和b满足(a-6)2+=0,求△ABC的周长.
变式1:若一条长为31 cm的细线能围成一边长等于7 cm的等腰三角形,则该等腰三角形的腰长为( )
A.7 cm B.9 cm C.7 cm或12 cm D.12 cm
变式2:已知等腰三角形的一边长是3,另一边长是方程+=1的解,则这个三角形的周长
是( )
A.10 B.11 C.10或11 D.7或8
变式3:在△ABC中,AB=8,且BC=2a+2,AC=22.
(1)求a的取值范围;
(2)若△ABC为等腰三角形,求这个三角形的周长.
答案
1.C
2.3 △ABD,△ACD △ACD,△ACB ∠ADC
3.C
4.等腰 解: 因为a+b+c=10,a=3,b=4,所以c=3,即a=c,所以△ABC为等腰三角形.
[点评] 要判断三角形的形状,可先通过计算得出三角形的三条边长,再比较各边长,判断其形状.
5.线段最短 > >
6.A 解: A项,5+7=12>10,能摆成三角形;
B项,3+4=7,不能摆成三角形;
C项,4+5=9<10,不能摆成三角形;
D项,1+2=3,不能摆成三角形.故选A.
7.C 解: 设第三边长为x cm,根据三角形的三边关系可得6-3
11-2
所以△ABC的周长为11+11+2=24.
10.解:若该等腰三角形的腰长为2 cm,则另外两边的长分别为2 cm,8 cm,根据三角形三边关系知不能构成三角形;
若等腰三角形的底边长为2 cm,则腰长为×(12-2)=5(cm),即另外两边的长分别为5 cm,5 cm.
综上,该等腰三角形的另外两边的长分别为5 cm,5 cm.
11.D 解: 根据三角形三边满足的条件:两边的和大于第三边,两边的差小于第三边,即可确定a+b-c>00,所以|aa+b-c0.故选D.
12.B 解: ①当长度分别为5,3,4时,能构成三角形,且最长边为5;
②当长度分别为2,6,4时,不能构成三角形;
③当长度分别为2,7,3时,不能构成三角形;
④当长度分别为6,3,3时,不能构成三角形.
综上所述,得到的三角形的最长边长为5.
13.D 解: 因为三条边长均为正整数,并且其中仅有一条边长为5,且它又不是最短边,所以:
①当5是最大的边长时,可能的情况有四种:4,2,5;4,3,5;4,4,5;3,3,5;
②当5是较大的边长时,可能的情况有六种:2,5,6;3,5,7;3,5,6;4,5,6;4,5,7;4,5,8.
综上,共十种情况,所以满足条件的三角形共有10个.
14.7 解: 因为a,b满足|a-7|+(b-1)2=0,所以a-7=0,b-1=0,解得a=7,b=1.因为6
因为a2-b2=ac-bc,
所以(a-b)(a+b)=c(a-b),
即(a-b)(a+b-c)=0.
因为a,b,c是△ABC的三边长,
所以a+b-c>0,
所以a-b=0,即a=b,
故△ABC为等腰三角形.
16.解:(1)因为(a-b)2+(b-c)2=0,
所以a-b=0,b-c=0,
所以a=b=c,
所以△ABC是等边三角形.
(2)因为a=5,b=2,且c为整数,
所以5-2
所以当c=4时,△ABC的周长有最小值,最小值为5+2+4=11;
当c=6时,△ABC的周长有最大值,最大值为5+2+6=13.
17.解:(1)> >
(2)AB+AC>BM+MN+NC.
延长BM交AC于点D,延长CN交BD于点E.
由(1)可得AB+AC>DB+DC>EB+EC,
即AB+AC>EM+BM+EN+NC=(EM+EN)+BM+NC>MN+BM+NC,
所以AB+AC>BM+MN+NC.
“串”题训练
例:解: 利用非负数的和为0,求出a=6,b=3,然后分情况讨论腰长为3或6,要考虑能不能构成三角形.
解:因为(a-6)2≥0,≥0,(a-6)2+=0,
所以
解得
若6为腰长,则△ABC的三边长分别为6,6,3,其周长为6+6+3=15;
若3为腰长,则此时△ABC的三边长分别为3,3,6,3+3=6,不能构成三角形.
综上所述,△ABC的周长为15.
变式1:D 解: 若腰长为7 cm,设底边长为x cm,则7+7+x=31,解得x=17,
此时三角形的三边长分别为7 cm,7 cm,17 cm.
因为7+7<17,
所以此三角形不成立;
若底边长为7 cm,设腰长为y cm.由题意,得
7+y+y=31,
解得y=12,
此时三角形的三边长分别为7 cm,12 cm,12 cm.
故选D.
变式2:C 解: +=1,解得x=4.
当等腰三角形的腰长为4,底边长为3时,这个三角形的周长为4+4+3=11;
当等腰三角形的腰长为3,底边长为4时,这个三角形的周长为4+3+3=10.
所以这个三角形的周长是10或11.
变式3:解:(1)由题意,得22-8<2a+2<22+8,
解得6
②若AC=BC,则三角形的三边长为8,22,22,此时三角形的周长为8+22+22=52.
综上所述,这个三角形的周长为52.
