沪科版数学八年级上册同步课时练习:12.4 综合与实践 一次函数模型的应用(word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步课时练习:12.4 综合与实践 一次函数模型的应用(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 420.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
12.4 综合与实践 一次函数模型的应用
知识点 建立一次函数模型,解决实际问题
1.皮球从高处落下时,弹跳高度b与下落高度d之间的关系如图下表所示:
下落高度d … 80 100 150 …
弹跳高度b … 40 50 75 …
则d与b之间的函数表达式为( )
A.d=b2 B.d=2b
C.d=b+40 D.d=b
2.某公司研发出一种新产品,每件成本为50元,该公司决定在某地进行试销售,结果发现每件产品的销售价格x(元)与日销售量y(件)之间存在一定的关系,如图示.猜想y与x之间的函数关系为( )
A.y=x B.y=x-20
C.y=-x+100 D.y=x
3.如图大拇指与小拇指尽量张开时,两指尖之间的距离称为指距.根据人体构造学最近的研究成果表明,一般情况下人的指距d和身高h成某种关系.下表是测得的指距与身高的一组数据:
指距d(cm) 20 21 22 23
身高h(cm) 160 169 178 187
根据上表解决下面这个实际问题:姚明的身高约为226 cm,可预测他的指距约为 .(结果精确到0.1 cm)
4.爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣的现象,即鞋子的码数y与鞋子的长度x(cm)之间存在着某种联系,经过收集数据,得到下表:
鞋长x(cm) … 22 23 24 25 26 …
码数y … 34 36 38 40 42 …
请你代替小明解决下列问题:
(1)根据表中数据,在同一平面直角坐标系中描出相应的点,你发现这些点在哪一种形上
(2)求出y与x之间的函数表达式,验证这些点的坐标是否满足函数表达式;
(3)当鞋的码数是41时,鞋长是多少
5.汽车行驶中,司机从判断出现了紧急情况到进行刹车时,这一段汽车走过的路程称为刹车反应距离.某研究机构收集了有关刹车反应距离的数据如图下表:
x 20 25 30 35 40 45 50 55 60 65 70 75 80
y 22 m 33 38.5 44 50 55 n 66 71 77 82.5 88
表中x为汽车行驶的速度(单位:英里/时),y为刹车反应距离(单位:英尺),m,n为丢失的数据.由表中给出的有序实数对,在平面直角坐标系中对应的点如图示.
(1)请用平滑的曲线顺次连接中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由;
(2)请利用估计得到的函数关系,求出表中m,n的值.
6.为提醒人们节约用水,及时修好漏水的水龙头,两名同学分别做了水龙头漏水试验,他们用于接水的量筒最大容量为100毫升.
试验一:小王同学在做水龙头漏水试验时,每隔10秒观察一次量筒中水的体积,记录的数据如图下表(漏出的水量精确到1毫升):
时间t(秒) 10 20 30 40 50 60 70
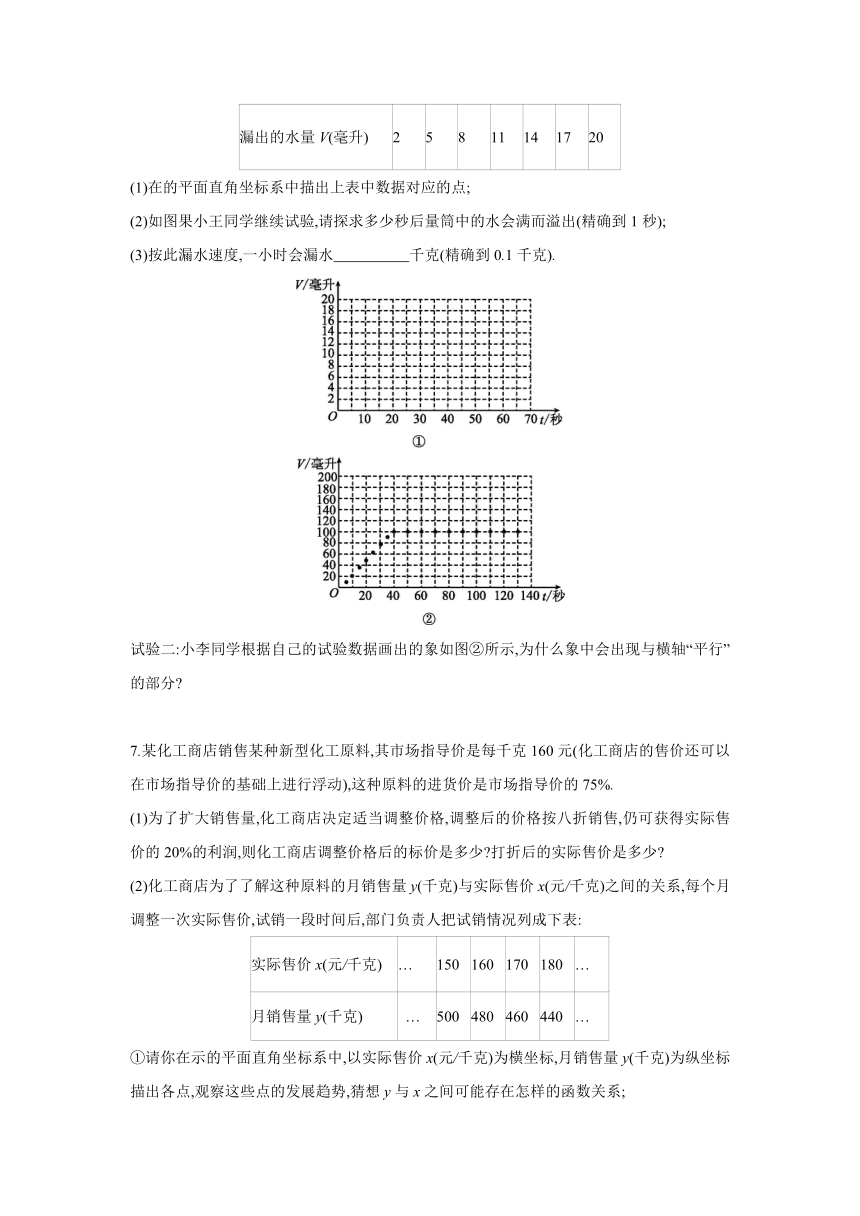
漏出的水量V(毫升) 2 5 8 11 14 17 20
(1)在的平面直角坐标系中描出上表中数据对应的点;
(2)如图果小王同学继续试验,请探求多少秒后量筒中的水会满而溢出(精确到1秒);
(3)按此漏水速度,一小时会漏水 千克(精确到0.1千克).
试验二:小李同学根据自己的试验数据画出的象如图②所示,为什么象中会出现与横轴“平行”的部分
7.某化工商店销售某种新型化工原料,其市场指导价是每千克160元(化工商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.
(1)为了扩大销售量,化工商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润,则化工商店调整价格后的标价是多少 打折后的实际售价是多少
(2)化工商店为了了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:
实际售价x(元/千克) … 150 160 170 180 …
月销售量y(千克) … 500 480 460 440 …
①请你在示的平面直角坐标系中,以实际售价x(元/千克)为横坐标,月销售量y(千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;
②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;
③若化工商店某月按同一实际售价共卖出这种原料450千克,请你求出化工商店这个月销售这种原料的利润是多少元.
答案
1.B
2.C 解: 根据这些点在一条直线上,猜想该函数为一次函数关系.
设一次函数的表达式为y=kx+b.
将点(60,40),(65,35)代入,得
解得则y=-x+100.
经检验,其他组数据也都满足.
所以y与x之间的函数关系为y=-x+100.
3.27.3 cm 解: 由表中数据猜测指距和身高是成一次函数关系的,设这个一次函数的表达式为h=kd+b,选前两组数据代入,得解得所以这个一次函数的表达式是h=9d-20,将后面两组数据代入,同样满足这个函数表达式.当h=226时,9d-20=226,解得d≈27.3.
4.解:(1)如图,这些点近似在一条直线上.
(2)y=2x-10,这些点的坐标都满足函数表达式,验证过程略.
(3)当y=41时,有2x-10=41,解得x=25.5,即当鞋的码数是41时,鞋长是25.5 cm.
5.解:(1)连线,如图所示.
观察象上除(45,50)和(65,71)两点略微偏离直线外,其他各点均在同一条直线上,
所以y与x的关系近似于一次函数关系.
(2)设直线的函数表达式为y=kx+b.
将点(20,22),(60,66)代入,
得解得
∴y=1.1x.
当x=25时,y=27.5,所以m=27.5;
当x=55时,y=60.5,所以n=60.5.
6.解:试验一:(1)描点如图所示.
(2)由(1)得V是t的一次函数.
设V与t之间的函数表达式为V=kt+b.
根据表中数据可知:
当t=10时,V=2;当t=20时,V=5.
所以解得
所以V=t-1.将其余各组数据代入上式验证,均成立,
所以V与t之间的函数表达式为V=t-1.
由题意,得t-1≥100,
解得t≥=336.
所以约337秒后量筒中的水会满而溢出.
(3)1.1
试验二:因为小李同学接水的量筒装满后水会溢出,量筒内的水位不再发生变化,所以象中会出现与横轴“平行”的部分.
7.解:(1)依题意,每千克原料的进货价为160×75%=120(元).
设化工商店调整价格后的标价为x元/千克,
则0.8x-120=0.8x×20%,解得x=187.5.
187.5×0.8=150(元/千克).
答:化工商店调整价格后的标价是187.5元/千克,打折后的实际售价是150元/千克.
(2)①描点画,如图,观察象,可知这些点在一条直线上,所以猜想y与x之间存在着一次函数关系.
②根据①中的猜想,设y与x之间的函数表达式为y=kx+b.
将(150,500)和(160,480)分别代入表达式,得
解得
所以y与x之间的函数表达式为y=-2x+800.
将(170,460)和(180,440)代入y=-2x+800,均成立,
即这些点都符合y=-2x+800的发展趋势.
所以①中猜想y与x之间存在着一次函数关系是正确的.
③当y=450时,x=175,
所以(175-120)×450=24750(元).
答:化工商店这个月销售这种原料的利润是24750元.
知识点 建立一次函数模型,解决实际问题
1.皮球从高处落下时,弹跳高度b与下落高度d之间的关系如图下表所示:
下落高度d … 80 100 150 …
弹跳高度b … 40 50 75 …
则d与b之间的函数表达式为( )
A.d=b2 B.d=2b
C.d=b+40 D.d=b
2.某公司研发出一种新产品,每件成本为50元,该公司决定在某地进行试销售,结果发现每件产品的销售价格x(元)与日销售量y(件)之间存在一定的关系,如图示.猜想y与x之间的函数关系为( )
A.y=x B.y=x-20
C.y=-x+100 D.y=x
3.如图大拇指与小拇指尽量张开时,两指尖之间的距离称为指距.根据人体构造学最近的研究成果表明,一般情况下人的指距d和身高h成某种关系.下表是测得的指距与身高的一组数据:
指距d(cm) 20 21 22 23
身高h(cm) 160 169 178 187
根据上表解决下面这个实际问题:姚明的身高约为226 cm,可预测他的指距约为 .(结果精确到0.1 cm)
4.爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣的现象,即鞋子的码数y与鞋子的长度x(cm)之间存在着某种联系,经过收集数据,得到下表:
鞋长x(cm) … 22 23 24 25 26 …
码数y … 34 36 38 40 42 …
请你代替小明解决下列问题:
(1)根据表中数据,在同一平面直角坐标系中描出相应的点,你发现这些点在哪一种形上
(2)求出y与x之间的函数表达式,验证这些点的坐标是否满足函数表达式;
(3)当鞋的码数是41时,鞋长是多少
5.汽车行驶中,司机从判断出现了紧急情况到进行刹车时,这一段汽车走过的路程称为刹车反应距离.某研究机构收集了有关刹车反应距离的数据如图下表:
x 20 25 30 35 40 45 50 55 60 65 70 75 80
y 22 m 33 38.5 44 50 55 n 66 71 77 82.5 88
表中x为汽车行驶的速度(单位:英里/时),y为刹车反应距离(单位:英尺),m,n为丢失的数据.由表中给出的有序实数对,在平面直角坐标系中对应的点如图示.
(1)请用平滑的曲线顺次连接中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由;
(2)请利用估计得到的函数关系,求出表中m,n的值.
6.为提醒人们节约用水,及时修好漏水的水龙头,两名同学分别做了水龙头漏水试验,他们用于接水的量筒最大容量为100毫升.
试验一:小王同学在做水龙头漏水试验时,每隔10秒观察一次量筒中水的体积,记录的数据如图下表(漏出的水量精确到1毫升):
时间t(秒) 10 20 30 40 50 60 70
漏出的水量V(毫升) 2 5 8 11 14 17 20
(1)在的平面直角坐标系中描出上表中数据对应的点;
(2)如图果小王同学继续试验,请探求多少秒后量筒中的水会满而溢出(精确到1秒);
(3)按此漏水速度,一小时会漏水 千克(精确到0.1千克).
试验二:小李同学根据自己的试验数据画出的象如图②所示,为什么象中会出现与横轴“平行”的部分
7.某化工商店销售某种新型化工原料,其市场指导价是每千克160元(化工商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.
(1)为了扩大销售量,化工商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润,则化工商店调整价格后的标价是多少 打折后的实际售价是多少
(2)化工商店为了了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:
实际售价x(元/千克) … 150 160 170 180 …
月销售量y(千克) … 500 480 460 440 …
①请你在示的平面直角坐标系中,以实际售价x(元/千克)为横坐标,月销售量y(千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;
②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;
③若化工商店某月按同一实际售价共卖出这种原料450千克,请你求出化工商店这个月销售这种原料的利润是多少元.
答案
1.B
2.C 解: 根据这些点在一条直线上,猜想该函数为一次函数关系.
设一次函数的表达式为y=kx+b.
将点(60,40),(65,35)代入,得
解得则y=-x+100.
经检验,其他组数据也都满足.
所以y与x之间的函数关系为y=-x+100.
3.27.3 cm 解: 由表中数据猜测指距和身高是成一次函数关系的,设这个一次函数的表达式为h=kd+b,选前两组数据代入,得解得所以这个一次函数的表达式是h=9d-20,将后面两组数据代入,同样满足这个函数表达式.当h=226时,9d-20=226,解得d≈27.3.
4.解:(1)如图,这些点近似在一条直线上.
(2)y=2x-10,这些点的坐标都满足函数表达式,验证过程略.
(3)当y=41时,有2x-10=41,解得x=25.5,即当鞋的码数是41时,鞋长是25.5 cm.
5.解:(1)连线,如图所示.
观察象上除(45,50)和(65,71)两点略微偏离直线外,其他各点均在同一条直线上,
所以y与x的关系近似于一次函数关系.
(2)设直线的函数表达式为y=kx+b.
将点(20,22),(60,66)代入,
得解得
∴y=1.1x.
当x=25时,y=27.5,所以m=27.5;
当x=55时,y=60.5,所以n=60.5.
6.解:试验一:(1)描点如图所示.
(2)由(1)得V是t的一次函数.
设V与t之间的函数表达式为V=kt+b.
根据表中数据可知:
当t=10时,V=2;当t=20时,V=5.
所以解得
所以V=t-1.将其余各组数据代入上式验证,均成立,
所以V与t之间的函数表达式为V=t-1.
由题意,得t-1≥100,
解得t≥=336.
所以约337秒后量筒中的水会满而溢出.
(3)1.1
试验二:因为小李同学接水的量筒装满后水会溢出,量筒内的水位不再发生变化,所以象中会出现与横轴“平行”的部分.
7.解:(1)依题意,每千克原料的进货价为160×75%=120(元).
设化工商店调整价格后的标价为x元/千克,
则0.8x-120=0.8x×20%,解得x=187.5.
187.5×0.8=150(元/千克).
答:化工商店调整价格后的标价是187.5元/千克,打折后的实际售价是150元/千克.
(2)①描点画,如图,观察象,可知这些点在一条直线上,所以猜想y与x之间存在着一次函数关系.
②根据①中的猜想,设y与x之间的函数表达式为y=kx+b.
将(150,500)和(160,480)分别代入表达式,得
解得
所以y与x之间的函数表达式为y=-2x+800.
将(170,460)和(180,440)代入y=-2x+800,均成立,
即这些点都符合y=-2x+800的发展趋势.
所以①中猜想y与x之间存在着一次函数关系是正确的.
③当y=450时,x=175,
所以(175-120)×450=24750(元).
答:化工商店这个月销售这种原料的利润是24750元.
